Математическая модель задачи

 

Математическая модель этой задачи имеет следующий вид. Максимизировать целевую функцию

при следующих ограничениях:

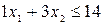– 1-е ограничение (на сырье),

– 2-е ограничение (на труд),

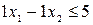– 3-е ограничение (спроса 1),

– 4-е ограничение (спроса 2),

.

Нулевые и единичные коэффициенты явно указаны в форму­лах ограничений для удобства ввода формул в Excel.

Решение задачи. Для решения этой задачи с помощью таблич­ного процессора необходимы следующие действия.

1. Создать в Excel таблицу вида:

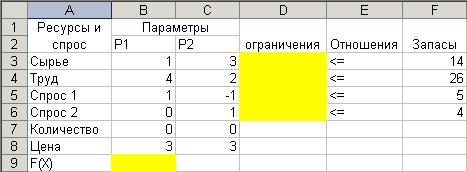
В затененных областях необходимо будет ввести формулы для целевой функции и линейных ограничений.

Значения переменных опорного плана (Количество) для Р₁ и Р₂ могут быть заданы вручную, что позволит ускорить процесс поиска решения. Если значения опорного плана не заданы, то программа определяет их автоматически.

2. В ячейке В9 для вычисления значения целевой функции ввести формулу =СУММПРОИЗВ(В8:С8;$В$7:$С$7), которая находит сумму попарных произведений ячеек с ценами (В8:С8) на ячейки со значениями параметров ($В$7:$С$7).

Координаты ячеек с количественными значениями парамет­ров Р₁ и Р₂ преобразуются к абсолютному виду для удобства дальнейшего копирования формулы в ячейки с ограничениями. Для такого преобразования необходимо при наборе формулы после выделения нужного диапазона ячеек в таблице (В7:С7) нажать клавишу F4.

3. Для задания ограничений по ресурсу Сырье в ячейку D3 скопировать формулу из ячейки В9, заменив диапазон цен (В8:С8) на диапазон параметров расхода сырья (ВЗ:СЗ). В результате в ячей­ке ЕЗ получится формула =СУММПРОИЗВ(ВЗ:СЗ;$В$7:$С$7). Для задания остальных ограничений скопировать вновь введен­ную формулу в ячейки D4, D5 и D6.

4. После создания таблицы с исходными данными установить курсор в ячейку с формулой целевой функции (В9) и выбрать в меню Сервис функцию Поиск решения. Затем заполнить поля в появившемся окне (см. рис. 1.4.1):

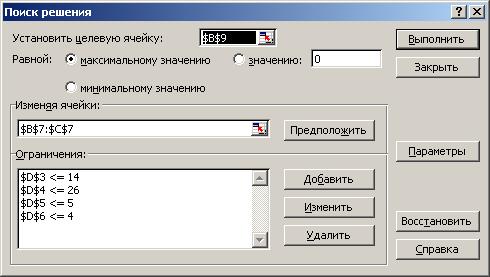
Рис. 1.4.1

 

· в поле Установить целевую ячейку должен появиться адрес ячейки с формулой целевой функции (в данном случае $В$9);

· установить переключатель вида оптимизации в поле Равной: в положение максимальное (минимальное) значение; при необ­ходимости найти максимум или минимум целевой функции;

· в поле Изменяя ячейки указать диапазон ячеек со значениями параметров задачи, выделив его в таблице. В данном примере это ячейки $В$7:$С$7;

· в поле Ограничения задать вид и значения ограничений. Для этого установить курсор в поле ввода ограничений и нажать кнопку Добавить. После чего в появившемся окне Добавление ограничения (см. рис. 1.4.2) ввести в поле Ссылка на ячейку адрес ячейки с формулой соответствующего ограничения (например, D3 для ресурса сырье). Затем ввести в поле Огра­ничение предельное значение соответствующего запаса (для ресурса сырье оно находится в ячейке F3) и выбрать вид от­ношения (<, >, = и т.п.).

После нажатия кнопки Добавить (или ОК для ввода послед­него ограничения) данное ограничение попадает в список ограничений задачи.

С помощью кнопок Удалить и Изменить можно удалять вы­деленные в списке ограничения или вносить в них исправления.

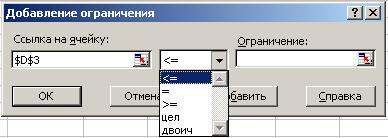
Рис. 1.4.2

5. После заполнения всех полей окна нажать кнопку Параметры и в открывшемся окне Параметры поиска решения (см. рис. 1.4.3) установить флажки Линейная модель для решения задачи линей­ного профаммирования и Неотрицательные значения, если такие ограничения накладываются на все переменные задачи.

В этом окне можно так же определить параметры процесса решения: предельное время поиска решения, максимальное ко­личество итераций, точность и т.п. Флажок Показывать результа­ты итераций позволяет по шагам следить за поиском решения. Флажок Автоматическое масштабирование включается в том случае, когда разброс значений параметров очень велик.

Рис. 1.4.3

6. Задав все параметры, нажать кнопку Выполнить для поиска решения задачи. Если решение найдено, то появляется окно с соответствующим сообщением (См. рис. 1.4.4). Результаты ре­шения могут быть сохранены в файле задачи в виде сценария или добавлены в виде отдельных листов Отчет по результатам, Отчет по устойчивости и Отчет по пределам. Для сохранения результатов в виде листов необходимо предварительно в поле Тип отчета выделить требуемые типы отчетов. В этом же окне можно отказаться от полученных решений и восстановить ис­ходные значения переменных.

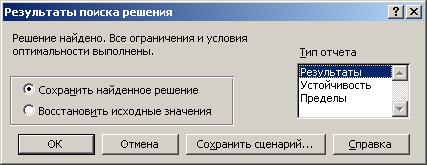
Рис. 1.3.4

Отчет по результатам приведен в табл. 1.3.1. В данном отче­те в графах Результат выводятся значения целевой функции и оптимального плана, а также значения исходного опорного пла­на (графа Исходное значение). Кроме того, указывается, какие ограничения являются связанными, т.е. ограничения с дефи­цитным ресурсом, а какие – нет (графа Статус), и приведены значения соответствующих дефицитов по всем ограничениям (графа Разница).

Таблица 1.4.1

Целевая ячейка (максимум)
Ячейка	Имя	Исходное значение	Результат
$В$9	F(X)
Изменяемые ячейки
Ячейка	Имя	Исходное значение	Результат
$В$7	Количество Р1
$С$7	Количество Р2

Ограничения

Ячейка	Имя	Значение	Формула	Статус	Разница
$D$3	Сырье Ограничения		$D$3<=14	связанное
$D$4	Труд Ограничения		$D$4<=26	связанное
$D$5	Спрос 1 Ограничения		$D$5<=5	не связан.
$D$6	Спрос 2 Ограничения		$D$6<=4	не связан.

Отчет по устойчивости выводится в следующей форме.

Таблица 1.4.2 Изменяемые ячейки

Ячейка	Имя	Результ. значение	Нормир. стоимость	Целевой коэфф.	Допуст. увелич.	Допуст. уменьш.
$В$7	Количество Р,
$С$7	Количество Р2					1,5
Ограничения
Ячейка	Имя	Резупьт. значение	Теневая цена	Огранич. прав, часть	Допуст. увелич.	Допуст. уменьш.
$D$3	Сырье огранич.		0,6		2,5
$D$4	Труд огранич.		0,6		7,5
$D$5	Спрос 1 огранич.				1Е+30
$D$6	Спрос 2 огранич.				1Е+30

 

В этом отчете выводятся допустимые отклонения (графы Допустимое увеличение и Допустимое уменьшение)от заданных значений ресурсов (графа Ограничения Правая часть)и целевых коэффициентов (графа Целевой коэффициент). В этих пределах изменения ресурсов можно производить оценку изменения це­левой функции с помощью двойственных оценок (см. [7]). Сами значения двойственных оценок ресурсов приведены в графе Тене­вая цена. Пределы изменения целевых коэффициентов задают об­ласти неизменности оптимального значения целевой функции.

Большие значения пределов изменения значений, например 1Е+30 (т.е. 10³⁰) для верхней границы на спрос, означают фак­тическое отсутствие верхней границы. Это характерно для неде­фицитных ресурсов, значение которых можно увеличивать до бесконечности.

 

Отчет по пределам имеет вид таблицы (см. табл. 1.4.3).

Таблица 1.4.3

Ячейка	Целевое имя	Значение
$B$9	R(X) P1
Ячейка	Изменяемое имя	Значение	Нижний предел	Целевой результат	Верхний предел	Целевой результат
$B$7	Количество Р1		#Н/Д	#Н/Д
$C$7	Количество Р2		1,894Е-12

 

В этом отчете приведены значения нижних и верхних преде­лов изменения переменных оптимального плана (графы Нижний предел и Верхний предел) и для них даны соответствующие опти­мальные значения целевой функции (графы Целевой результат).

 

Варианты заданий для решения задачи принятие решений

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: