Практические критерии статической устойчивости.

 

2.9.1 Анализ статической устойчивости по критерию .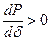

Для системы, в которой станция связана с системой через относитель­но длинную линию электропередачи, расчет по критерию дает результаты, хорошо приближающиеся к действительности. Расчет ведут в последовательности:

1) определяют выражение мощности, от­даваемой генератором удаленной станции;

2) находят выражение для производной ;

3) из условия 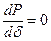определяют угол, соответствующий предельному режиму;

4) подставив это значение угла в выра­жение для мощности, вычисляют предел мощности, после чего, учтя нормативный коэф­фициент запаса по устойчивости, определяют мощность, которую можно пере­дать от удаленной станции без наруше­ния статической устойчивости.

В этих расчетах неявнополюсный генератор замещается той или иной эдс в зависи­мости от вида АРВ(.

У явнополюсных нерегулируемых генерато­ров эдс при изменении нагрузки меняется. При приближенной оценке рекомендуется упрощать задачу, проводя расчет как для неявнополюсной машины и принимая постоян­ной эдс, приложенную за сопротивлением 0,85 .

В случае необходимости насыщение гене­раторов можно приближенно учесть, приняв для неявнополюсных машин , для явнополюсных машин .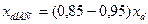

Расчеты, проводимые при замене нагрузки постоянным сопротивлением и приводящие к некоторому завышению предела передаваемой мощности, должны рассматриваться только как ориентировочные. Учет действительных харак­теристик нагрузки может производиться или только в отношении влияния изменений напря­жения на шинах нагрузки на потребляемую ею мощность, или в отношении одновремен­ного учета изменений напряжения и частоты в системе.

При проверке устойчивости по критерию сложных систем полагают эдс всех станций неизменными (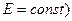 и вычисляют синхронизирующие мощности станций, наибо­лее «опасных» в отношении возможности нарушения устойчивости. При этом могут вычисляться синхронизирующие мощности по­очередно между станциями или между груп­пами станций. Задача всегда носит несколько неопределенный характер: при вычислении синхронизирующей мощности какой-либо стан­ции делаются достаточно грубые допущения относительно поведения остальных станций, распределения мощностей между ними и т. п.

В системе, состоящей из двух станций, относительное ускорение в функции изменения угла ₁₂ при уже сделанном допущении о поведении нагрузки однозначно определяет предел по устойчивости. Изменение взаимного угла между двумя станциями в сложной системе не дает такой определенности, по­скольку каждой комбинации относительных углов остальных станций соответствуют свои значения мощностей станций системы. Синхро­низирующая мощность каждой станции, в том числе и исследуемой, зависит от характера изменения всех относительных углов. В прак­тике расчетов для устранения указанной не­определенности обычно принимают одно из следующих допущений:

1) постоянство углов всех генераторных станций, кроме данной;

2) постоянство активных мощностей, вы­даваемых всеми станциями, кроме двух.

При первом допущении угол 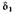удаленной станции, отсчитанный относительно синхронно вращающейся оси, получает перемещение (рис.2.31). Абсолютные углы всех остальных станций и т. д. остаются при этом неизменными. Все относительные углы первой станции получают одинаковое изменение и т. д. Относительные углы осталь­ных станций сохраняют свои значения, поэтому и т.д.

 

Рис. 2.31. Векторная диаграмма эдс генераторов сложной энергосистемы

 

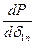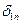Такому определенному из­менению относительных углов соответствуют определенные изменения мощностей всех стан­ций, включая первую. Критерием устойчивости является знак синхронизирующей мощности , где - угол между эдс данной станции и эдс любой другой станции системы.

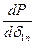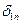Второе допущение предполагает изменение активных мощностей лишь двух станций, в то время как мощности остальных станций принимаются неизменными. Критерием устой­чивости и в этом случае служит знак производной , где - угол между векторами эдс станции, которая нагружается (1), и балансирующей станции (п).

2.9.2 Анализ статической устойчивости по критерию .

Этот практический критерий стати­ческой устойчивости применяют при исследо­вании систем с концентрированной нагрузкой, содержащих одну или несколько узловых точек, по отношению к которым станции и нагрузки имеют примерно одинаковую электрическую удаленность.

Сущность метода применительно к схеме, показанной на рис.2.32, заключается в следующем. Каждая из нагрузок или 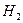, присоединенных к узловой точке а, обладает определенной характеристикой . Объединив все нагрузки, получим результирующую реактивную нагрузку узла в исход­ном режиме и ее зависимость в функции напряжения

.

 

 

Рис. 2.32 Схема концентрированной энергосистемы с нагрузкой в узле.

 

 

Изменение нагрузки узла в исходном ре­жиме на 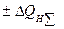дает возможность найти новую характеристику (. Таким образом, можно получить семейство характеристик нагрузки (рис. 2.33). От каждого из генераторов к точке а поступает реак­тивная мощность. В случае замещения какого-либо генератора постоянной эдс Е реактив­ная мощность, поступающая на шины на­грузки, определяется уравнением

,

где п — номер генератора;

— сопротивление данной ветви генератора до точки а.

Зависимость суммарной реактивной мощ­ности, поступающей от генераторов,

может быть представлена также в виде се­мейства характеристик, каждая из которых относится к некоторому исходному режиму. В любом установившемся режиме ,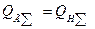

т. е. имеет место пересечение этих характеристик. Очевидно, что могут быть два вида пересечения характеристик: такое, как в точках 1 — 3, где при отклонении напряжения

или такое, как в точках 4 — 6, где

.

 

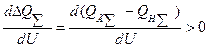Рис.2.33 Характеристики мощности генераторов и нагрузки узловой точки энергосистемы.

 

В первом случае (точка 1), когда система устойчива, так как при

любом случайном уменьшении напряжения на появляется избыток реактивной мощности , приводящей к увеличению напряжения, проявляющемуся до тех пор, пока напряже­ние не восстановится. Во втором случае (точка 6) система неустойчива.

Таким образом, критерий устойчивости системы будет заключаться в требовании выполнения условия

.

 

 

2.9.3 Анализ статической устойчивости по критерию .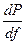

В некоторых системах, например имеющих электрические печи, практический критерий 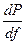может оказаться решающим для определения устойчивости режима. Кри­терий 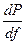аналогичен критерию .

При проверке устойчивости по критерию 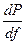строят зависимости и

, по которым определяют небаланс мощности и его знак. При построении харак­теристик автоматическое регулирование часто­ты может учитываться или не учитываться (в зависимости от условий расчета).

Энергосистема должна работать так, чтобы некоторые изменения (ухудшения) режимных параметров не приводили к нарушению ее устойчивости, т. е. необходим запас. Запас по устойчивости оценивается соотношением пара­метров исходного и предельного (по устойчи­вости) режимов.

Следует, однако, иметь в виду, что исход­ные данные по параметрам системы и ее
режима известны лишь с той или иной степенью точности, а возникновение аварий­ных ситуаций в системе носит случайный характер, поэтому результатам одиночных рас­четов не всегда придают решающее значение. В ряде случаев здесь при­ходится проводить дополнительные исследо­вания, связанные с учетом неточности исход­ных данных.

 

 

⇐ Предыдущая9101112131415161718Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: