О применении табличного метода анализа в семасиологических исследованиях

Применение таблиц и схем в исследованиях любого рода давно известно, однако лингвисты XIX и начала XX в. использовали графику очень скупо и лишь в иллюстративных цепях. Примером тому может служить известный треугольник Г. Стерна, вершины которого символизируют слово, значение и предмет, а стороны — связи между ними. Существуют и другие варианты треугольника, но все они без исключения только фиксируют те отношения между объектами исследования, которые автор уже нашел каким-то другим путем; иллюстрируя мысль, они помогают читателю понять и запомнить ее.

И наше время в графике ищут средств моделирования и такого представления материала, которое удовлетворяло бы не только иллюстративным, но и эвристическим целям. Другими словами, речь идет о поисках новых путей улучшения обозримости материала.

Здесь уместно привести слова известного математика Д.Пойя, который писал: «Законченная математика, изложен­ная в законченной форме, выглядит как чисто доказательная, состоящая только из доказательств. Но математика в процессе создания напоминает любые другие человеческие знания, находящиеся в процессе создания. Вы должны догадаться о математической теореме, прежде чем вы ее докажете; вы должны догадаться об идее доказательства, прежде чем вы его проведете в деталях. Вы должны сопоставлять наблюдения и следовать аналогиям; вы должны пробовать и снова пробовать»¹.

Как помочь лингвисту представить результаты наблюдений таким образом, чтобы их можно было легко сопоставить, заметить имеющиеся аналогии и таким образом построить гипотезы, с тем чтобы в дальнейшем подтвердить их на речевом материале или отбросить?

Таблицы с количественной оценкой материала, которые все больше проникают в лингвистические исследования, уже являются эвристическими и должны позволить сопоставить наблюдения, но они очень несовершенны как основа для

 

24

25

догадки, так как позволяют наблюдать сочетания только двух переменных. Эти таблицы часто приходится делать очень громоздкими или делить на несколько групп, что затрудняет их обозримость. Интерпретация содержания таблицы, комбинатор­ные возможности которой ограничены двумя измерениями, ложится целиком на автора. Комбинированный эффект несколь­ких факторов заметить очень трудно. Оценка получается субъективной. Опыт показывает, что значение этого субъектив­ного фактора довольно велико и что сам исследователь, как правило, замечает далеко не все то, что дают ему им же собранные факты. Это и заставляет искать таблицы такого типа, который мог бы дать более сильные эвристические возможности и показать сочетаемость большего числа переменных.

Широкие перспективы в этом отношении обещает теория графов, которая интенсивно проникает в лингвистику, правда, с некоторым опозданием по сравнению с ее проникновением в экономику, биологию или химию, не говоря уже о чисто абстрактных математических науках. Теория графов обладает значительной эвристической силой, но в настоящем сообще­нии мы остановимся не на ней, а на матрицах Вейтча, заимствованных нами у техников.

Матрицы Вейтча оказались очень полезными в базирующейся на математическом аппарате булевой алгебры теории логического синтеза релейных устройств — новом разделе теории автоматического управления². Попытаемся показать, что они могут быть также эффективным средством лингвистического анализа.

Матрица определяется как прямоугольная упорядоченная таблица элементов, состоящая из m столбцов и n строк. Между элементами матрицы (помимо отношений следования и предшествования) существуют и еще какие-то заранее опре­деленные отношения. В дальнейшем изложении мы будем называть матрицу Вейтча, использованную в виде таблицы слов, наборов признаков и т.п., решеткой Вейтча, а отражающую ее матрицу, элементами которой являются числа — просто матрицей.

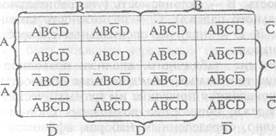
Предлагаемый табличный метод обнаружения типичной модели состоит в применении решеток Вейтча, имеющих следующий вид: большой квадрат разделен на 16 более мелких

26

квадратов (клеток), каждый из которых характеризует одну из 16 возможных комбинаций четырех пар взаимоисключаю­щих признаков. Верхняя половина большого квадрата соот-ветствует тем случаям, когда признак А=1, т.е. когда этот признак налицо. Нижняя же половина этого квадрата — тому случаю, когда А=0, т.е. когда Ā=1. Левая и правая половины большого квадрата представляют случаи, когда В или соот-ветственно ¯В равно 1. Две центральные строки соответствуют тому случаю, когда С=1, а верхняя и нижняя — тому случаю, когда ¯С равно 1. Для признаков D и ¯D это соответственно средние и наружные столбцы. Каждый малый квадрат пред-ставляет тогда такие комбинации, как AB¯C¯D, ĀB¯CD, A¯B¯CD и т.д., каждая из которых отличается от соседней только в одном каком-нибудь признаке³.

Таблица для двух пар признаков содержит 2² = 4 клетки, для трех пар 2³ = 8 клеток. Вид таблицы можно упростить, охватив соответствующей фигурной скобкой только строки и столбцы, в которых дифференциальный признак имеет зна-чение 1. Тогда за пределами этих клеток соответствующий Признак имеет значение 0 (см. табл. 1).

Представление комбинаций признаков рассматриваемой лингвистической структуры любого уровня в виде графической функции четырех переменных, могущих иметь значение 1 или 0, удобно сочетается с учением об оппозициях, которым мы обязаны Н.С.Трубецкому и которое может плодотворно применяться и в семасиологии⁴.

Таблица 1 Решетки Вейтча для четырех нар признаков

27

Под оппозицией, как известно, понимается отноше­ние частичного различия между частично сходными элемен­тами языка. Оппозиции, один член которых характеризуется наличием, а другой отсутствием дифференциального признака, называются привативными, или бинарными. Бинарные оппо­зиции соответствуют двузначной математической логике. Создателем алгебры логики, т.е. символического метода вывода логических отношений, был английский математик Джордж Буль⁵. Двоичной, или булевой, переменной называют такую переменную, которая может иметь лишь одно из двух значений. Эти два значения принято обозначать либо 1 и 0, либо словами «истина» и «ложь». Последний способ исполь­зуется в исчислении высказываний. Математический аппарат, относящийся к двузначным логическим функциям, является основой, на которую опирается все построение математичес­кой логики и ее прикладное использование в машинах для переработки информации. Многозначная логика разработана пока еще мало.

Бинарное построение лингвистических систем вызывало много возражений, в особенности применительно к фоноло­гии⁶. Однако, поскольку все другие типы оппозиций могут быть сведены к бинарным, не существует состоятельных аргументов в пользу принципиальной ограниченности послед­них⁷. Описанная здесь методика пользуется бинарными оппозициями.

Решетки Вейтча удобно применить с классификационной целью. Так, для разбиения всего множества нарицательных существительных английского языка на лексико-грамматичес­кие разряды мы применяли следующие признаки: А — исчисляемость, В — склоняемость (употребительность формы притяжательного падежа), С — возможность замещения мес­тоимением it, D — наличие специальных словообразователь­ных суффиксов.

Применение табличного анализа позволило получить классы существительных, объединенные общностью форм, в которых проявляются присущие им грамматические категории числа и падежа, общностью возможных слов-заместителей, факультативно, определенным набором аффиксов. При этом оказалось, что грамматические свойства разряда предопреде-

28

 

ляют и семантическую общность принадлежащих к нему слов⁸. Так, например, существительные actor, adventurer, agent, artist И т.п. попали во вторую клетку первой строки, составленной для указанных выше признаков решетки, и могут характери-зоваться набором 1101. В первой клетке второй строки оказываются существительные canary, cat, caterpiller, cow и т.п. Им соответствует набор 1110. Таким образом, существительные по формальным признакам разбиваются на два разряда, различаясь свойствами замещения и морфемного состава. Первый разряд включает существительные-названия лица второй — названия прочих живых существ. Всего для современного английского языка было получено восемь разрядов нарицательных существительных.

Попытаемся показать применимость табличного анализа с эвристической целью для разработки круга задач семасиологии, которым до сего времени уделялось сравнительно мало внимания, а именно — для исследования семантической системы английского языка с точки зрения особенностей и типичных свойств семантической структуры слов того или иного лексико-грамматичсского класса.

Под семантической структурой при этом пони-мается множество возможных для слова лексико-семантических вариантов с определенными на нем отношениями. Особое внимание будет обращено на связи типа значения с грамматическими характеристиками варианта.

Множество лексико-семантичсских вариантов слова обра-зуют структуру в том смысле, что все элементы множества, помимо того что все они находятся между собой в отношении эквивалентности, определяющем их принадлежность к данному множеству, связаны между собой еще каким-то типом отноше­ний. В нашем случае — это отношение семантической произ-водности, которое понимается в синхронном плане: каждый вариант может быть объяснен через один из остальных.

Теоретическая важность задачи представляется очевидной, поскольку речь идет о предсказуемости семантических свойств:

зная одно из значений слова и его принадлежность к тому или иному лексико-грамматическому разряду, возможно с известной степенью вероятности предсказать и другие типы его значений.

29

Для нужд прикладной лингвистики, и в частности для научного обоснования методики обучения иностранным язы­кам, важно выяснить зависимость характера совпадения в одном слове разных типов лексических значений от морфо­логического строения этого слова и других его грамматических свойств.

Такая предсказуемость может быть достигнута, если будет найдена некоторая простая модель для словарного состава данного языка, в нашем случае — английского⁹.

Такую модель можно получить при помощи решеток Вейтча, применяя их для характеристики семантической структуры отдельных слов и для семантической характеристики целых разрядов, с последующим их сопоставлением.

Рассмотрим простейший вариант применения решетки и матрицы для представления семантической структуры отдель­ного слова.

Следует подчеркнуть, что речь идет не об описании семантики слов (делается допущение, что словари достаточно точно отражают словарный состав), а лишь о новом пред­ставлении этого описания, опирающемся на существующие лексикографические сведения и данные о релевантных струк­турных противопоставлениях. Цель заключается в том, чтобы найти хотя бы в первом приближении типичные для разных классов слов объединения лексико-семантических вариантов.

Для анализа выбрано слово kid, принадлежащее в исход­ном значении к упомянутому выше второму лексико-грамма-тическому разряду (одушевленные существительные не назва­ния лица). Словарь Хорнби¹⁰ дает три варианта: «козленок» — с прямым значением, переносное — «лайка» (кожа), принад­лежащее к разряду вещественных существительных, и «малыш» — стилистически и эмоционально окрашенный вариант, исчисляемый, соотносимый не только с местоиме­нием it, но и с местоимениями he и she и, следовательно, принадлежащий к разряду названий лиц. Добавим к этому четвертый, грамматически связанный с употреблением только во множественном числе и указанный другими словарями вариант «лайковые перчатки». На табл. 2 показана решетка для слова kid и ее матрица (для обозначения матрицы применяются двойные вертикальные линейки).

30

Таблица 2 Табличный анализ семантической структуры слова kid

A - Лексико-грамматические варианты, принадлежащие второму

разряду.

Ā - Лексико-грамматические варианты, принадлежащие другим

разрядам.

B - Вариантыс переносным значением.

¯B - Варианты без переноса (прямое значение).

C - Эмоционально окрашенные варианты.

¯C - Эмоционально нейтральные варианты.
D - Варианты со свободным значением.

¯D - Варианты с грамматически связанным значением.

 

S =

0 0 10

0 0 0 0

0 1 0 0

 

 

		козленок
	малыш
лайковые перчатки (только множ. ч)	лайка (кожа)

 

A

 

 

Ā

 

D

 

D

Пример представляется интересным тем, что очень ясно показывает эфемерность нашего представления о парадигме как основе единства слова. Четырем вариантам слова соответствуют три разных лексико-грамматических разряда и, следовательно, разные парадигмы.

Составляя модель для семантической характеристики разряда, мы определяем статистически, какое число слов данного разряда может быть репрезентативным, и выбираем это количество подряд по словарю или в равных долях из разных частей словаря, чтобы обеспечить случайность выборки. Далее либо составляются и затем складываются матрицы¹¹ на каждое обследованное слово, либо делаются большие решетки и каждое слово заносится туда столько раз и в такие клетки, как это определяется описанием

31

его вариантов в словаре. Заполненные решетки и матрицы разных разрядов затем сопоставляются, что позволяет сделать вывод о типичных особенностях каждого разряда (см. табл. 3).

Статистическая обработка матриц позволяет перейти от эвристической задачи на нахождение к задаче на доказатель­ство и подтвердить скрытую за кажущейся хаотичностью словаря систему с ее статистическими закономерностями.

Выбранный для иллюстрации разряд позволяет получить общую схему зоосемии, характерную для современного анг­лийского языка. Варианты с переносным значением образуют две большие группы: самая большая, охватывающая около 40% всех рассмотренных случаев, содержит эмоционально окрашенные метафорические переносы со значением лица, обладающего действительными или традиционно приписыва­емыми данному животному, большей частью отрицательными, свойствами поведения или характера.

Во второй клетке третьей строки встречаются такие перенос­ные варианты, как chameleon — «человек, меняющий свои убеждения как хамелеон окраску», colt, употребляясь примени­тельно к молодому человеку, насмешливо подчеркивает его неопытность, drone — «бездельник, живущий подобно трутню за счет других». Во вторую клетку четвертой строки — эмоционально нейтральные варианты с переносным значением — включаются метафорические названия предметов, напоминающих соответст­вующих животных или своей формой (cockle, scallop, crane), или характером движения (caterpillar) и тд. Около 25% рассмотренных примеров составляют слова, метонимически обозначающие то, что использует человек в данном животном: его мясо (chicken, crab), мех (sable, ermine), кожу (kid, chamois). Если сопоставить данную таблицу с аналогичными таблицами для других разрядов, то можно установить, что слова, которые принадлежат к этому разряду в своем основном значении, часто переходят в произ­водных значениях в другие разряды, обозначая людей, вещества, предметы, группы. Характерной особенностью оказывается много­численность эмоционально окрашенных производных вариантов. Проблема выбора дифференциальных признаков для сема­сиологических исследований — одна из наиболее актуальных и трудных в современной лингвистике. Набор признаков, пере­численных выше, не следует понимать диахронически, как типы

32

изменений значений. Такое заблуждение может возникнуть из-за принятых терминов. В действительности речь идет о чисто синхронных логических противопоставлениях по сход-ству смежности и объему понятий, выраженных в разных вариантах слова на современном этапе развития языка.

Таблица 3

Заполнение решетки Вейтча для производных вариантов существительных,

которые в основном варианте принадлежат ко второму лексико-грамматическому разряду

В

	1. python — удав	1. boar — боров 2. cat — живот- ное из семей- ства кошачьих 3. cow — самка слона, кита и т.п. 8. pup — дете- ныш лисы, вол- ка и т.п.	1. fowl — (с пред- шест. прил. и без s во множ. числе) — крупная птица
	1. chick — девчонка 2. pup — молокосос 3. rat — негодяй 44. sheep — роб- кий человек
1. ermines — горно- стаевая мантия 2. horse — кавалерия 3. sables — соболье манто	1. boar — мясо кабана 2. cafl — телячья кожа 3. ermine — мех горностая 43. canary — канареечный цвет

D

33

 

А — Варианты, принадлежащие ко второму лексико-грамматическо-

му разряду

В — Варианты с переносным значением

С — Эмоционально или стилистически окрашенные варианты D — Варианты с грамматически свободными значениями

0 18 1 0 0 0 0 0 44 0 0 3 43 0 0

Одно из преимуществ предлагаемой процедуры и состоит в том, что она хорошо сочетается с количественной обработ­кой, поскольку над матрицами можно производить различные арифметические действия.

Как нетрудно заметить, в предложенных примерах взяты признаки разных уровней. Так, наряду с привычными лекси­кологу семантическими противопоставлениями переноса и отсутствия переноса (генерализации и специализации), эмо­ционального и эмоционально нейтрального, включены и морфологические признаки, такие, как наличие специального, характерного для данного разряда суффикса или его отсутст­вие, исчисляемость и неисчисляемость. Такой подбор при­знаков нарушает требование классической дескриптивной лингвистики проводить все операции в пределах одного уровня. Это требование основано на том, что в пределах одного уровня формализация материала делается в рамках совершенно четкой аксиоматики¹². Скрещение же уровней такой четкости не дает. Поэтому многомерная модель неиз­бежно оказывается менее точной, чем модель в пределах одного уровня. Однако реальная действительность языка тоже многомерна, и для того чтобы получить всестороннее пред­ставление о языке, приходится на некоторых этапах синтези­ровать сделанное в разных планах, на разных уровнях.

Предложенная табличная процедура анализа, удобная для наглядного представления соотношений между любыми дво­ичными переменными, и возможности ее применения в лингвистике далеко не ограничиваются описанием семанти­ческой структуры слова.

ПРИМЕЧАНИЯ

1 Пойя Д. Математика и правдоподобные рассуждения. Т. 1: Пер. с англ. M., 1957. С. 10.

2 См.: Колдуэлл С. Логический синтез релейных устройств: Пер. с англ. М., 1962.

3 См.; Ричарде Р.К. Арифметические операции на цифровых вычилительных машинах: Пер. с англ. М., 1957. С. 78.

4 См.: Трубецкой Н.С. Основы фонологии: Пер. с нем. М., I960.

5 О значении работ Дж.Буля см.: Шеннон Кл. Работы по теории информации и кибернетики: Пер. с англ. М., 1963. С. 13.

6 См, например: Мартине А. Принцип экономии в фонетических пениях: Пер. с франц. М., 1960. С. 15.

7 См: Исаченко А.В. Бинарность, привативные оппозиции и пиитические значения // Вопросы языкознания. 1963. № 2.

8 См.: Арнольд И.В. Семантическая структура слова в современ-ном английском языке и методика ее исследования. Л., 1966.

9 Под моделированием понимается выявление и обобщение наиболее существенных особенностей и связей в интересующем иследователяя участке реальной действительности и замена этого участка действительности формулой, схемой, графом, физическим устройством и т.д. Проблемы моделирования привлекают внимание многих лингвистов. (См., например: Пиотровский Р.Г. Моделирова-ние фонологических систем и методы их сравнения. М.; Л.: Наука, 1966

¹⁰ The Advanced Learner's Dictionary of Current English. First publ. By A.S.Hornby, E.V.Gatenby, H.Wakefield. London: Oxford Univ. Press, 1948.

^l1 При сложении нескольких матриц получается новая матрица, элементы которой являются суммами соответствующих элементов отдельных матриц.

¹² Формализация при этом понимается, конечно, не как исследование языка без учета семантики, а как представление обобщающего описания строгим аксиоматическим способом, не допускающим двусмысленности. (См.: Откупщикова М.И. Об одном возможном способе построения формальной морфологии // Мате-реальны по математической лингвистике и машинному переводу: Сб. П. П., 1963. С. 62.

 

34

35

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: