 |
Моделирование числовых последовательностей и рядов
|
|
|
|
Числовые последовательности представляют собой множества чисел. Если каждому числу n из натурального ряда чисел 1,2,3, …, n…поставлено в соответствие вещественное число xn, то множество чисел x1, x2, x3, …, xn … называют числовой последовательностью. Числа x1, x2, x3, … называют, членами последовательности, xn- n-ным или общим элементом, а число n –его номером.
Таким образом, последовательность представляет собой множество пронумерованных элементов. Последовательность задана, если известен способ получения любого ее элемента. Последовательность обозначается символом {xn}. Например, символ {1/n} обозначает последовательность чисел 1, 1/2, 1/3, 1/4, …, 1/n. В общем случае для создания массива элементов последовательности нужно выполнить следующие действия:
1. Создать массив, содержащий множество чисел натурального ряда;
2. Ввести в ячейку формулу последовательности, делая в ней адресные ссылки на ячейки, содержащие номера элементов последовательности
3. Скопировать введенную формулу во все другие ячейки массива.
Пример создания последовательности {1/n}, и последовательности {n/(n+1)}.

Для создания наиболее часто встречающихся последовательностей, таких как арифметическая или геометрическая прогрессия, табличный процессор имеет специальный инструмент “Прогрессия”, который находится: линейка Главная → Редактирование → Заполнить → Прогрессия.
Технология вычисления пределов числовых последовательностей
Технологию приближенного вычисления предела числовой последовательности рассмотрим на примере. Пусть требуется найти предел числовой последовательности
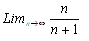

Технология моделирования числовых рядов
Числовым рядом называется бесконечная последовательность чисел u1, u2 , …, un…, соединенных знаком сложения 
|
|
|
Ряд считается заданным, если известен его общий член un=f(n). Сумма n первых членов ряда называется частичной суммой ряда. Для вычисления частичной суммы ряда в электронной таблице нужно выполнить следующие шаги:
1. Вычислить n первых членов числовой последовательности
2. Вычислить сумму членов числовой последовательности
Численное вычисление пределов функций
В математике для нахождения пределов функций применяются специальные приемы, в частности такой, как разложением числителя и знаменателя на сомножители и некоторые другие. Используя электронную таблицу, можно применить следующую технологию:
Ø В ячейку рабочего листа ввести формулу, соответствующую выражению функциональной зависимости, в которой значение аргумента указывается адресной ссылкой на ячейку, которая содержит аргумент
Ø В ячейку, предназначенную для записи аргумента функции, ввести число, максимально близкое к точке, в которой вычисляется предел функции.
Пример.


Найти предел функции
Подбор параметра
Реализация различных экономических и финансовых проектов и задач, зачастую требует решения проблемы подбора одного параметра так, чтобы другой параметр принял требуемое значение. То есть, если известен целевой показатель вычисления формулы, но не известны входные значения, позволяющие получить его, то в MS Excel используется инструмент Подбор параметра. Этот инструмент является средством решения задач анализа данных «что если», когда путем перебора одного значения достигается необходимое значение исследуемой функции (критерии оптимальности).
Итак, для того, чтобы определить значение, удовлетворяющее требуемому значению критерия оптимальности, необходимо вывести инструмент Подбор параметра в списке команд «Анализ «что-если»» в группе команд Работа с данными ленты ДАННЫЕ (рис.5).
|
|
|

Рис.5. Работа с данными (Анализ «что если»)
Для того, чтобы применить инструмент Подбор параметра (рис. 6) необходимо настроить соответствующие поля диалогового окна:
1. Установить в ячейке — ссылка на ячейку с исследуемой формулой;
2. Значение — планируемое значение, в виде частного экстремума;
3. Изменяя значение ячейки — ссылка на ячейку с подбираемым параметром;
4. Нажать ОК.

Рис. 6. Окно Подбор параметра
Пример 1. Требуется определить, каким должен быть курс евро, чтобы имея в наличии 3678 рублей, купить 90 евро.
Решение (уравнение для упомянутой задачи имеет вид х * 90 = 3678, где х — искомый курс доллара, для которого в MS Excel создадим модель):
1. В ячейке А2 должно быть подобрано значение курса доллара (предварительно ячейка пустая).
2. В ячейку B2 вводим формулу: =А2 * 90, предварительный итог которой 0.
3. Запустив инструмент Подбор параметра, необходимо в поле Установить в ячейке указать ссылку на ячейку B2, в поле Значение ввести 3678, а в поле Изменяя значение ячейки указать ссылку на ячейку А2 (рис. 7) (ответ: 40,866667).

Рис. 7. Результат решения примера 1
Пример 2. Определить, под какую процентную ставку необходимо сделать вклад в банк в сумме 500000 рублей, с ежемесячным начислением процентов, чтобы за 4 года накопить на счету 1000000 рублей? Модель задачи представлена на рисунке 8.
С помощью встроенной финансовой функции (БС), позволяющей вычислять будущую стоимость, определим ее значение при условных 10% (744 677,05 р.).

Рис. 8. Расчет процентной ставки
Решение:
1. Установите курсор в ячейку B6, где расположена функция (формула) и запустите инструмент Подбор параметра.
2. В поле Установить в ячейке, должна быть ссылка на ячейку B6.
3. В поле Значение введите 1000000.
4. В поле Изменяя значение ячейки установите ссылку на ячейку В3 (рис9) (ответ: 17,45%).

Рис. 9. Подбор параметра р асчета процентной ставки
В результате получим искомое значение процентной ставки 17,45% (рис. 10).
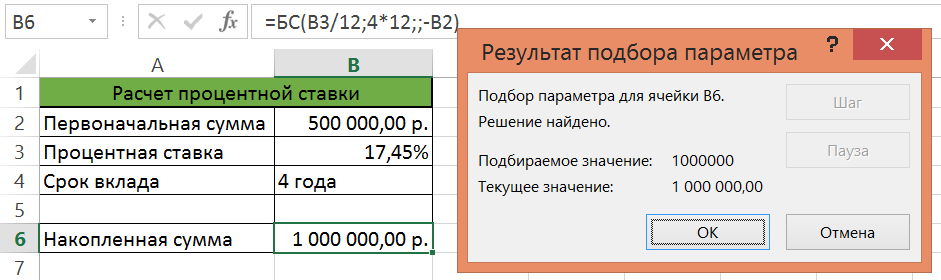
Рис. 10. Расчет процентной ставки после подбора параметра
Итак, инструмент Подбор параметра, подбирает конкретный показатель, при котором требуемый результат достигает определенного значения.
|
|
|


