 |
Алгоритм метода интегральной суммы
|
|
|
|
Казанский государственный
Энергетический университет
М.П. ЖЕЛИФОНОВ
МАТЕМАТИКА
ПРАКТИКУМ ПО ТЕМЕ
«ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ»
Методическое пособие
Для самостоятельной работы студентов
Казань 2004
УДК 517.31
ББК 22.161.1
Ж51
Желифонов М.П.
Математика. Практикум по теме «Определенный интеграл». Казань: Казан. гос. энерг. ун-т, 2004.
Приведены краткие теоретические сведения по методу интегральной суммы, рассматриваются примеры, приводящие к определенному интегралу, и дается подборка задач для самостоятельного решения.
Предназначен для самостоятельного, более глубокого изучения студентами основных приемов интегрирования.
ã Казанский государственный энергетический университет, 2004
ЦЕЛЬ РАБОТЫ
Приобретение студентами КГЭУ практических навыков по вычислению определенных интегралов. Кроме кратких теоретических сведений по методу интегральной суммы в работе детально рассматриваются конкретные примеры, приводящие к определенному интегралу, и дается подборка задач для самостоятельного решения.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Метод интегральной суммы
Опр. Аддитивной величиной наз. параметр физической системы Р, который можно представить как сумму его значений от всех составных частей системы P = 
pi.
Например, площадь фигуры, объем и масса тела, длина пройденного пути. Разбиение на составные части в этих случаях совершенно произвольно. Разделение пространственного объекта можно довести до уровня отдельной точки, затем определить в ней значение нужного параметра, но вот вычислить сумму бесконечно большого числа таких слагаемых прямым суммированием нельзя. Приходится вводить предельный процесс. Такой подход к решению многих задач наз. методом интегральной суммы.
|
|
|
Задача. Вычислить площадь круга радиуса R.
Строим вписанный в круг n – угольник и соединяем его вершины с центром. Тогда 
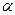АОС = 2 
= 2 
/n, AC = 2 AB = 2 R sin 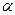, SAOC = AB BO = R sin 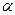R cos 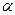= = ½ R 2sin 2 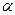. Площадь многоугольника Sn = n SAOC в пределе n 
переходит в площадь круга S = lim Sn =
=½ R 2 lim n sin 2 / n = R 2 lim sin(2 / n)/(2 / n) = R 2.
Последовательность действий: имеем основную фигуру, разделяем ее на n участков, вычисляем площадь одного треугольника, вычисляем общую площадь треугольников, переходим к пределу. Эта процедура носит универсальный характер.
Алгоритм метода интегральной суммы
1. Исследуемая аддитивная система разделяется на n однотипных участков.
2. Для каждого участка устанавливается некоторое приближенное значение аддитивного параметра pi .
3. Проводится суммирование приближенных значений аддитивного параметра по всем n участкам P(n) = 
pi.
4. Переход к пределу lim P (n) = P при n дает точное решение задачи, т.е. определяет значение искомого параметра для всей системы
Опр. Интегральной суммой наз. сумма всех приближенных значений аддитивного параметра, определенных для каждого из n участков на которые была разделена исследуемая система.
Опр. Предел интегральной суммы, полученной путем разбиения пространственного объекта на составные части, наз. интегралом (определенным). Это главный параметр суммы.
Вид суммы и её предела определяется условиями задачи и числом использованных переменных. Существуют двойные, тройные, криволинейные, поверхностные интегралы.
Площадь криволинейной трапеции
Опр. Фигура ограниченная графиком функции y = f (x)на промежутке[ a,b ], осью Ох и двумя перпендикулярами, восстановленными из точек a и b наз. криволинейной трапецией.
Метод интегральной суммы:
1) Отрезок [ a, b ]разделим на n равных частей точками xi = a + i 
x, где i = 0,1,2, …, n и x = (b – a)/ n. Из точек xi восстановим перпендикуляры и соединим их прямыми | | оси Ох на высоте f (
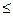
i ), где xi 
i 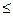xi+1. Получим вспомогательную, ступенчатую фигуру, составленную из прямоугольников. 2) Площадь одного прямоугольника f ( i ) xi. 3)Площадь всей вспомогательной фигуры, т.е. интегральная сумма, равна
|
|
|
Sn = f ( i) xi (1)
Чем больше n, тем точнее приближение, а предел n должен дать точный результат
Опр. Определенным интегралом от функции f ( x ) на промежутке[ a,b ]наз. предел интегральной суммы, полученный путем разбиения промежутка на малые участки.
lim 
f ( i) xi =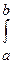 
f (x) dx (2)
Здесь а – нижний предел, b – верхний предел, а сам символ повторяет основные элементы интегральной суммы. Введен Лейбницем.
Геометрический смысл определенного интеграла – площадь криволинейной трапеции. Геометрический смысл интегральной суммы – площадь вспомогательной фигуры.
|
|
|
