 |
Основные свойства определенного интеграла
|
|
|
|
10  A f (x) dx = A
A f (x) dx = A  f (x) dx
f (x) dx
Постоянный множитель выносится за знак интеграла, т.к. он может быть вынесен за знак суммы.
20  [ f (x) + g (x)] dx =
[ f (x) + g (x)] dx =  f (x) dx +
f (x) dx +  g (x) dx
g (x) dx
Интеграл от суммы функций равен сумме интегралов, т.к. предел от суммы функций равен сумме пределов.
30  f(x) dx =
f(x) dx = 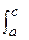 f(x) dx =
f(x) dx =  f(x) dx (a < c < b)
f(x) dx (a < c < b)
Интеграл на промежутке [ a,b ]можно представить как сумму интегралов, взятых по произвольным участкам [ a,b ]. ( Смотри геометрический смысл определенного интеграла).
40  f (x) dx = -
f (x) dx = - 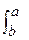 f (x) dx Перестановка пределов меняет общий знак.
f (x) dx Перестановка пределов меняет общий знак.
50  f(x) dx = 0 (Нет ширины у трапеции.)
f(x) dx = 0 (Нет ширины у трапеции.)
60 Теорема о среднем.  f (x) dx = f (
f (x) dx = f ( ) (b – a)
) (b – a)
Определенный интеграл от непрерывной функции всегда можно представить как произведение полного приращения аргумента ( b – a ) на значение функции в некоторой промежуточной точке f ( ), т.к. для любой трапеции можно построить прямоугольник такой же ширины и площади (a
), т.к. для любой трапеции можно построить прямоугольник такой же ширины и площади (a 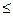

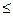 b )
b )
Пр. Вычислить площадь трапеции f (x) = xk на интервале[0, a ]
1) Разбиение [0, a ]точками xi = (a/n) i,где i = 1,2,… n, с шагом  x = (a/n).
x = (a/n).
2) Площадь i – ого прямоугольника f ( i )
i )  xi = (xi) k
xi = (xi) k  x = (a/n) k+1 i k
x = (a/n) k+1 i k
3) Интегральная сумма Sn =  f (
f ( i)
i)  xi = (a/n) k+1
xi = (a/n) k+1  i k
i k
4) Доказано, что  i k = n k+1/(k+ 1)+
i k = n k+1/(k+ 1)+  Am nk-m,
Am nk-m,
где Am – коэффициенты.
При переходе к пределу n  не нулевой вклад в Sn дает только первое слагаемое и площадь трапеции равна S = lim Sn = ak+ 1 /(k+ 1 ).
не нулевой вклад в Sn дает только первое слагаемое и площадь трапеции равна S = lim Sn = ak+ 1 /(k+ 1 ).
Отсюда легко получить площадь трапеции на произвольном интервале [ a, b ].Достаточно записать разность площадей трапеций на интервалах [0, b ]и [0, a ]
Sab = bk+ 1/(k +1) - ak +1/(k +1)
Если вычислять площадь трапеции от произвольной функции f ( x ) на интервале [0, a ]методом интегральной суммы,то приходится в f ( x ) заменять х на ( a/n ) i и суммировать сложное выражение Sn = (a/n)  f ((a/n) i),что удается в редких случаях. К счастью, существует более простой способ определения предела интегральной суммы. В последнем примере связь между исходной функцией f (x) = xk и результатом S(x) = xk +1/(k +1)оказалась простой S’ (x) = f (x). Ниже покажем, что такая связь справедлива и для произвольной функции f ( x ).
f ((a/n) i),что удается в редких случаях. К счастью, существует более простой способ определения предела интегральной суммы. В последнем примере связь между исходной функцией f (x) = xk и результатом S(x) = xk +1/(k +1)оказалась простой S’ (x) = f (x). Ниже покажем, что такая связь справедлива и для произвольной функции f ( x ).
|
|
|
Определенный интеграл с переменным верхним пределом
Такой интеграл имеет вид Ф (х) =  f (t) dt, является функцией от х и определяет площадь криволинейной трапеции переменной ширины ( х – а ). Возьмем производную от этой функции
f (t) dt, является функцией от х и определяет площадь криволинейной трапеции переменной ширины ( х – а ). Возьмем производную от этой функции
Ф’ (х) = lim  Ф (х) /
Ф (х) /  x при
x при  x
x  0
0
Ф (х +  x) - Ф (х) =
x) - Ф (х) = 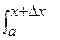 f (t) dt -
f (t) dt -  f (t) dt =
f (t) dt =
=  f (t) dt +
f (t) dt +  f (t) dt -
f (t) dt -  f (t) dt = f (c)
f (t) dt = f (c)  x,
x,
где с - точка на промежутке [ x, x+  x ]по теореме о среднем. Перейдем к пределу
x ]по теореме о среднем. Перейдем к пределу  x
x  0
0
Ф’ (х) = lim  Ф (х) /
Ф (х) /  x = lim f (c)
x = lim f (c)  x /
x /  x = f (c) = f (x)
x = f (c) = f (x)
 x
x  0
0  x
x  0
0
т.е. интеграл с переменным верхним пределом является одной из первообразных для подынтегральной функции, т.к. Ф’ (х) = f (x) (3).
Формула Ньютона – Лейбница
Это центральная теорема математического анализа. Она делает замену сложной процедуры вычисления пределов интегральной суммы на процедуру вычисления первообразных.
Теорема. Определенный интеграл от непрерывной функции f ( x ) на промежутке [ a,b ]равен разности значений первообразных этой функции F (x)на концах отрезка  f (x) dx = F (b) - F (a)(4)
f (x) dx = F (b) - F (a)(4)
Доказательство. Имеем функцию f ( x ), ее первообразную F (x)и строим функцию Ф (х) =  f (t) dt, которая также является первообразной функции f ( x ) по условию (3). Т.о., имеем две первообразных, которые могут отличаться только на константу
f (t) dt, которая также является первообразной функции f ( x ) по условию (3). Т.о., имеем две первообразных, которые могут отличаться только на константу
Ф (x) = F (x) + C (5)
Значение константы С находим из (5) при x = a:
 f (t) dt = F (a) + C = 0или C = - F (a)
f (t) dt = F (a) + C = 0или C = - F (a)
Теперь равенство (5) принимает вид  f (t) dt = F (x) - F (a)и при x = b переходит в формулу Ньютона – Лейбница (4).
f (t) dt = F (x) - F (a)и при x = b переходит в формулу Ньютона – Лейбница (4).
Вычисление работы
Работа по перемещению тела по прямой на расстояние S под воздействием постоянной силы F равна A = F S. Сила может зависеть от величины смещения: F = f (x).Например, силу растяжение пружины описывает закон Гука: F = k x. В этом случае расчет произведенной работы делают методом интегральной суммы.
|
|
|
1) Участок пути движения тела вдоль Ох от а до b разбивают на n отрезков длиной  x = (b – a) / n;2) Работа при перемещении вдоль одного отрезка равна f (
x = (b – a) / n;2) Работа при перемещении вдоль одного отрезка равна f ( i)
i)  x, где f (
x, где f ( i) - среднее значение силы для i – ого отрезка; 3) Сумма по всем отрезкам равна A (n) =
i) - среднее значение силы для i – ого отрезка; 3) Сумма по всем отрезкам равна A (n) =  f (
f ( i)
i)  x и совпадает с интегральной суммой (1); 4) Переход к пределу n
x и совпадает с интегральной суммой (1); 4) Переход к пределу n  дает точное решение задачи
дает точное решение задачи
lim  f (
f ( i)
i)  xi = А =
xi = А = 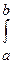 f (x) dx (1)
f (x) dx (1)
Физический смысл определенного интеграла - работа по перемещению тела в поле переменных сил по прямой.
Вычислим этот предел для случая закона Гука. Пусть  i - крайние точкиотрезков, тогда f (
i - крайние точкиотрезков, тогда f ( i ) = k
i ) = k  i = k [ a +
i = k [ a +  ],
],  x =
x =  и интегральная сумма равна
и интегральная сумма равна
A (n) = k  = k(b-a) {
= k(b-a) { 
 1 +
1 + 
 i }=
i }=
= k(b-a) { a + 
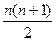 }
}
Переход к пределу A = lim A (n) = k (b-a) { a + (b-a)/ 2} = k(b2 – a2)/ 2
Формула Ньютона – Лейбница A = k 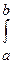 x dx = k x 2/2 | ab = k (b2 – a2)/ 2
x dx = k x 2/2 | ab = k (b2 – a2)/ 2
Теорема о среднем: A = k(b – a) (b + a)/ 2, т.е. среднее значение силы
F ( ) = k(b + a)/ 2.
) = k(b + a)/ 2.
Приемы интегрирования
Метод замены переменной при вычислении определенного интеграла по формуле Ньютона-Лейбница требует дополнительной операции - переопределения пределов интегрирования.
Пр. 
 dx =
dx = 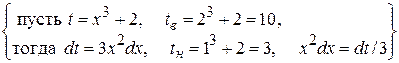 =
=
= 1/3 
 = - 1/3 1/ t |310 = 7/90 кв. ед.
= - 1/3 1/ t |310 = 7/90 кв. ед.
Задачи для самостоятельного решения (1)
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ; 7)
; 7)  ;
;
8)  ; 9)
; 9)  ; 10)
; 10) 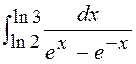 ; 11)
; 11)  12)
12) 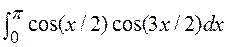 ; 13)
; 13)  ; 14)
; 14)  ;
;
|
|
|


