 |
Вычисление площади боковой поверхности и объема тела вращения.
|
|
|
|
Криволинейную трапецию, ограниченную неотрицательной функцией y = f (x)на [ a, b ] вращаем вокруг оси Ох и получаем цилиндрическое тело вращения. Определим площадь его боковой поверхности и объем методом интегральной суммы.
1) Вращение криволинейной трапеции предыдущего рисунка приведет к вспомогательной фигуре - последовательности усеченных конусов с радиусами оснований f (xi)и наклонными длинной li. 2) Боковая поверхность и объем каждого такого конуса (цилиндра) равны
Si = 2 
li (f (xi) + f (xi- 1))/2; Vi = f (xi)2 
xi
3) Просуммируем Si, Vi и получим две интегральные суммы
S (n) = 2 
li f (xi); V (n) = f (xi) 2 xi
4) Переход к пределу n 
дает решение задачи
S бок = lim S (n) = 2 
f (x) 
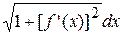(17)
V = lim V (n) = f 2(x) dx (18)
Пр. Определить площадь боковой поверхности и объем кругового конуса высоты h и радиуса основания r.
Решение. Уравнение образующей y = (r/h) x,где 0 < x < h. Тогда y’ = r/h, 
= 
S бок = 2 
r/h x dx = r 
= rl
V = (r/h)2 x 2 dx = h r 2 / 3
Задачи для самостоятельного решения (6)
Найти объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями: 1) y 2 = 2 px, x = a;2) y = x 2, y = 
;
3) x – y + 1 = 0, y = cos x, y = 0; 4) y = - x 2 + 8, y = x 2;
5) y = sin x, y = 0, x = 0, x = ; 6) y = - x 2 + 9, y = x 2
Найти объем тела, образованного вращением вокруг оси Оy фигуры, ограниченной линиями: 1) y = 4 – x 2, y = 0, x 
0; 2) y = x 2, y = 0, x = 1, x = 2.
Пр. Найти объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями: y = - x 2 + 8, y = x 2.
Решение. 1) Вычислим точки пересечения линий:
x 2 = 4, (-2;4), (2;4); 2) Начертим Рис.
3) Опр. пределы интегрирования: -2 
x 
2;
4) V = V 1 – V 2 = 
{ y 12(x) – y 22(x)} dx = {(8 – x 2)2 – x 4} dx =
= (64 x – 16 x 3/3) |-22 = 528 /3
Устные экзаменационные вопросы
по теме: «Неопределенный и определенный интегралы»
1. Опр. первообразной функции и неопределенного интеграла.
|
|
|
2. Перечислить названия элементов, входящих под знак неопределенного интеграла.
3. Сколько первообразных имеет каждая функция и почему?
4. Перечислить основные свойства неопределенного интеграла.
5. Объяснить инвариантность формы дифференциала сложной функции и неопределенного интеграла.
6. Что такое непосредственное интегрирование?
7. В чем заключается идея метода замены переменных?
8. Вывод формулы интегрирования по частям.
9. Основная теорема алгебры.
10. Опр. рациональной алгебраической дроби. Переход от неправильной к правильной дроби.
11. Записать формулу разложения рациональной алгебраической дроби на сумму простейших дробей.
12. Общее правило при линейной замене переменных.
13. Перечислить основные виды замены переменных в интегралах от тригонометрических функций.
14. Правила вычисления интегралов с линейными и квадратичными иррациональностями.
15. Опр. аддитивной величины.
16. Алгоритм метода интегральной суммы.
17. Опр. интегральной суммы.
18. Опр. криволинейной трапеции.
19. Опр. определенного интеграла. Его геометрический и физический смысл.
20. Перечислить основные свойства определенного интеграла. Теорема о среднем.
21. Определенный интеграл с переменным верхним пределом. Его вид и общее свойство.
22. Доказать формулу Ньютона-Лейбница. Ее значение в мат. анализе.
23. Опр. несобственного интеграла 1 и 2 рода. Общее правило вычисления интеграла от разрывных функций.
24. Общие правила вычисления площади плоской фигуры.
25. Площадь криволинейного сектора в полярных координатах. Записать интегральную сумму и интеграл.
26. Длина произвольной дуги. Записать интегральную сумму и интеграл.
27. Боковая поверхность и объем тела вращения. Записать интегральную сумму и интеграл.
Марат Павлович Желифонов
МАТЕМАТИКА
Практикум по теме «Определенный интеграл»
|
|
|
(Кафедра высшей математики КГЭУ)
Редактор издательского отдела Г.Я. Дарчинова
________________________________________________________________
Изд. лиц. № 03480 от 08.12.00 Темплан издания КГЭУ 2004 г.
Подписано к печати Формат 60 х 84/16
Гарнитура «Times» Вид печати РОМ Бумага «Business»
Физ. печ. л. 1 Усл. печ. л. 0,93 Уч-изд. л. 1,06
Тираж 500 Заказ
________________________________________________________________
Издательский отдел КГЭУ
420066, Казань, Красносельская, 51
________________________________________________________________
Типография КГЭУ
420066, Казань, Красносельская, 51
|
|
|
