 |
Зависимость интенсивности разрушений
|
|
|
|
от температуры в зоне контакта деталей
Взаимодействие контактирующих поверхностей носит вероятностный характер, обусловленный случайностью механических воздействий на детали и расположения микрорельефа поверхности. Поэтому и зависимости интенсивности разрушения от температуры, как и от других факторов, носят стохастический характер. По результатам аналитических исследований можно установить вид (характер) детерминирующей составляющей этих стохастических процессов.
Согласно первому закону термодинамики работа А трения преобразуется в теплоту q и внутреннюю энергию узла трения D Е

| (3.1) |
Экспериментально установлено [88, 182-184], что основная часть работы трения преобразуется в теплоту, а незначительная (менее 1% при окислительном изнашивании) запасается поверхностными слоями трущихся материалов при их деформации и разрушении. Как видно из (3.1), зависимость количества теплоты от работы трения можно принять практически линейной.
Повышение температуры поверхности трения и масла вследствие преобразования работы трения в теплоту в определенных пределах вполне допустимо. При этом наблюдается установившееся допустимое изнашивание поверхностей трения. При критической температуре, определяемой свойствами масла [1-3, 18, 26, 59, 67, 131, 143, 151], оно теряет свои смазочные свойства вследствие химической десорбции (разложения) и происходит изменение условий (вида) трения, что сопровождается резким повышением интенсивности изнашивания.
Рассмотрим сначала зависимость интенсивности изнашивания деталей сопряжения со смазкой на примере подшипников скольжения, так как этот тип сопряжений наиболее часто встречается в агрегатах автомобилей и других машин. Кроме того, закономерности этого узла справедливы и для других типов сопряжений. Обычно режим работы подшипника скольжения оценивают комплексной характеристикой режима
|
|
|
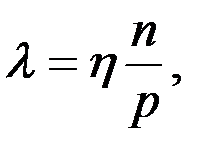
| (3.2) |
где h — абсолютная вязкость масла; п — частота вращения вала; р — давление, воспринимаемое подшипником.
Из типичной зависимости коэффициента трения f от характеристики режима работы подшипника l, приведенной на рис.2.3., при жидкостном трении (при l>lK) коэффициент трения изменяется незначительно.
При анализе характеристики l можно было бы сделать вывод о том, что постоянное значение l можно обеспечить одновременным пропорциональным увеличением р и п. Однако при этом возрастает температура в зоне трения, что при критической температуре приводит к резкому изменению условий трения и возрастанию коэффициента трения и интенсивности изнашивания.
При постоянных р и п характеристика l с ростом температуры уменьшается вследствие снижения вязкости масла. Обычно вязкостно-температурная характеристика масла описывается несколькими уравнениями [1, 2, 26, 81, 151]
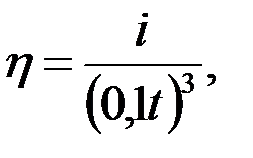
| (3.3) |
где i - характеристическое число, зависящее от типа масла; t - температура, °С.
Зависимость кинематической вязкости h от температуры может быть выражена эмпирическим уравнением Вальтера
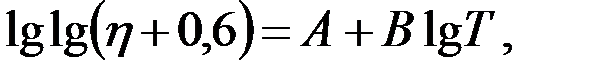
| (3.4) |
где h — кинематическая вязкость, сСт; А и В— константы, зависящие от масла; Т — абсолютная температура, °К.
Можно использовать и экспоненциальное уравнение [131]
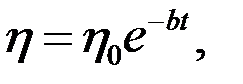
| (3.5) |
где hо — вязкость масла при t = 0, b — параметр, зависящий от типа масла (индекса вязкости).
Если допустить, что температура в масляном слое между шейкой и вкладышем пропорциональна температуре вкладыша, то с ростом температуры будет снижаться минимально допустимая для обеспечения жидкостного трения толщина масляного слоя (ТМС) hmin из-за вязкости h [84, 85]

| (3.6) |
где d - диаметр шейки вала; S - диаметральный зазор; с - поправка Гюмбеля на конечную длину подшипника (c=(d+l)/l), l - длина шейки вала.
|
|
|
Уравнение (3.6) можно записать в виде
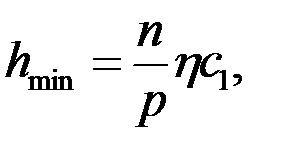
| (3.7) |
где с1 - экспериментальный параметр, зависящий от конструкции и состояния подшипника (c1=d2/18,36Sc).
Снижение толщины масляного слоя ведет к повышению вероятности контакта микровыступов поверхностей трения. Зависимость эту в определенных пределах ТМС можно считать линейной, что можно пояснить схемой взаимодействия микровыступов поверхностей трения (рис.3.3)
Как видно из схемы (рис.3.3, а), при ТМС, большей суммы двух средних высот микровыступов поверхностей, вероятность взаимодействия теоретически равна нулю (практически же, из-за переменности режимов, больше нуля). Взаимодействие начинается с величины h0, равной сумме средних высот микровыступов (рис.3.3, б). При дальнейшем сближении поверхностей (снижение h) вероятность взаимодействия микровыступов (их количество) возрастает (рис.3.3, в).
При изменении h от нуля до h0 можно считать, что количество контактирующих микровыступов N прямо пропорционально h, то есть
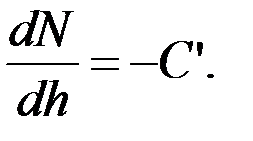
| (3.8) |
Знак минус перед коэффициентом пропорциональности С' свидетельствует о снижении N с ростом h, следовательно

| (3.9) |
где N0 — количество контактирующих микровыступов при h = 0.
В этих условиях контакта можно считать, что интенсивность изнашивания поверхностей трения прямо пропорциональна количеству контактирующих микровыступов, поэтому зависимость (3.9) справедлива и для интенсивности (скорости) изнашивания в виде
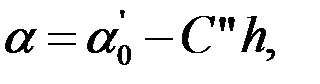
| (3.10) |
где 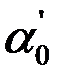 - интенсивность изнашивания при h=0 (то есть при сухом трении); С" — коэффициент пропорциональности.
- интенсивность изнашивания при h=0 (то есть при сухом трении); С" — коэффициент пропорциональности.
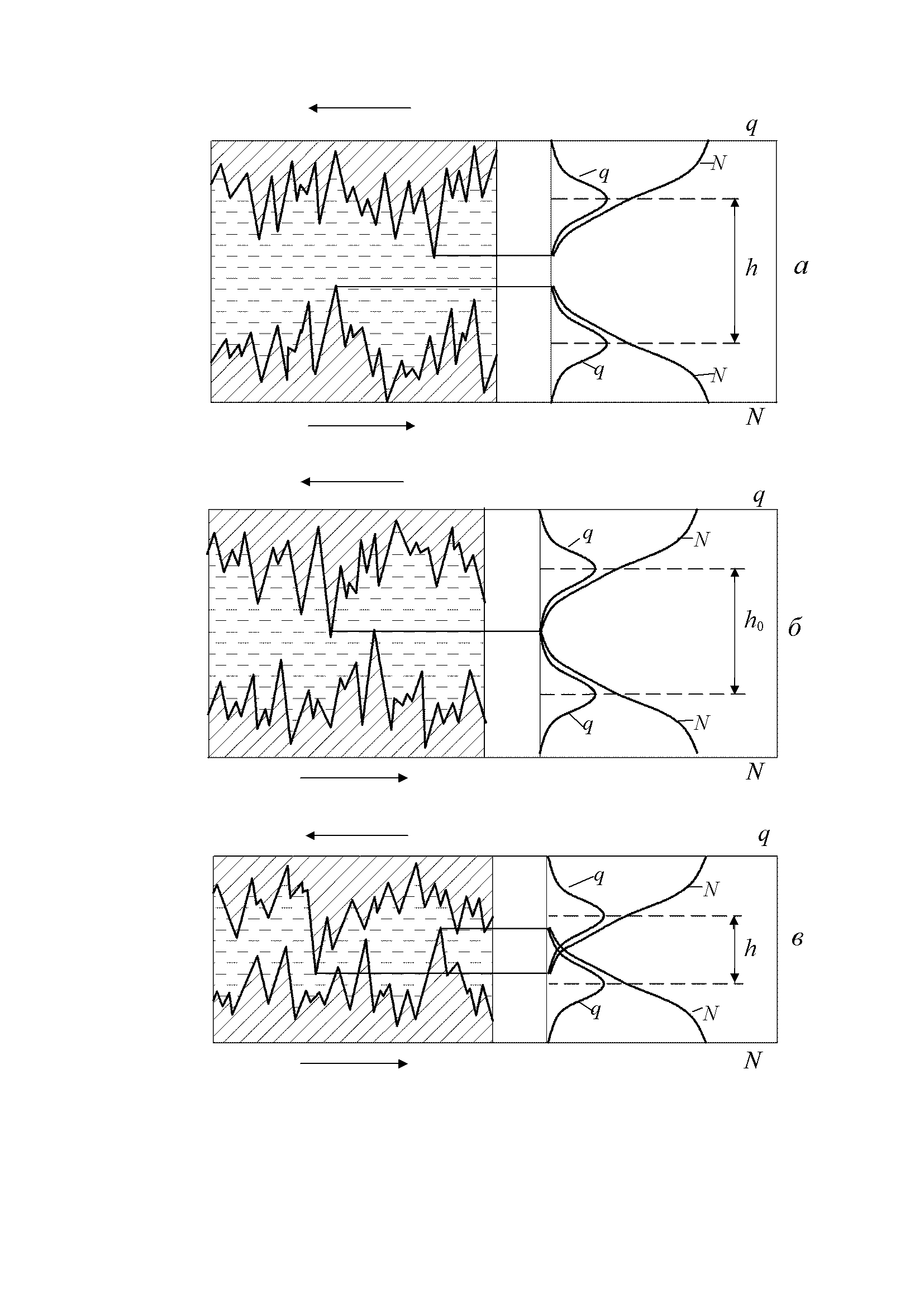
Рис.3.3. Схема взаимодействия микровыступов поверхностей трения
деталей при снижении средней толщины масляного слоя h: q - плотность вероятности высоты микровыступов; N- число контактирующих выступов (а - h>ho; б - h= h0; в - h<h0)
С учетом приведенных зависимостей (3.5), (3.7), (3.10) зависимость интенсивности изнашивания от температуры tП в зоне трения будет следующая
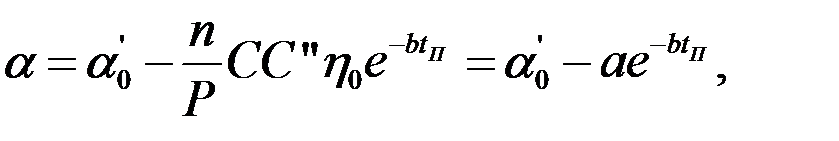
| (3.11) |
где а - параметр, определяемый конструкцией, состоянием, режимом работы узла трения при tП= 0 (рис.3.4).

| Рис.3.4. Зависимости интенсивности изнашивания от температуры поверхности трения: 1 - функциональная, 2 - аппроксимирующая |
Снижение темпа роста интенсивности изнашивания при увеличении температуры (рис.3.4) обусловлено формой вязкостно-температурной характеристики. Поскольку при выводе зависимости (3.11) принят ряд допущений о линейности зависимости N от h и a от N, которые в ряде случаев могут быть недостаточны вследствие многофакторного влияния, то зависимость a от tПможно описать в рассматриваемых пределах до критической температуры tПК линейной зависимостью
|
|
|
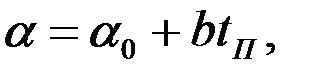
| (3.12) |
где a0 - интенсивность изнашивания при tП = 0, b - изменение a на единицу температуры поверхности или масляной пленки.
В самом деле, по мере снижения ТМС повышается число контактирующих микровыступов, причем, при нормальном распределении высоты микровыступов до средней высоты dN/dh возрастает, а при экспоненциальном распределении - во всем диапазоне от h0до h=0. При прямо пропорциональной зависимости a от N это ведет к росту da/dh, следовательно da/dtП будет снижаться, как в зависимости (3.11), то есть приходим к формуле (3.12).
С другой стороны, с повышением числа контактирующих микровыступов N при снижении h уменьшаются нагрузки на каждый выступ, что увеличивает их долговечность, и, следовательно, снижает интенсивность изнашивания. Это способствует снижению da/dh, а, следовательно, и da/dtП, как в зависимости (3.11). От соотношения этих двух противоположных факторов зависит форма зависимости a от tП.
Как показывают экспериментальные данные, выполненные с использованием точной методики измерения износа деталей и параллельных испытаний [43, 50], в допустимых пределах температуры поверхности трения и масляной пленки (от 40 до 160°) зависимость интенсивности изнашивании от температуры поверхности трения или масляной пленки линейная (3.12). Зависимости a от tП приведены на рис.3.6.
Параметры зависимости (3.12) действительны только до критической температуры масляной пленки, которая для моторных и трансмиссионных масел находится в пределах 140-160°С. О резком повышении интенсивности изнашивания после критической температуры свидетельствуют многочисленные экспериментальные данные [23, 87, 88].
|
|
|

Рис.3.6. Зависимость интенсивности изнашивания от температуры поверхности трения: а - шейка вала лабораторной установки при нагрузке (1 - 40Н; 2 - 80Н; 3 - 160H; 4 - 320H); б - коренные шейки двигателя
Это обусловлено снижением твердости и других свойств материала при повышении температуры [23, 153, 161] (рис.3.7), а также зависимостью износостойкости e, а, следовательно, и интенсивности изнашивания 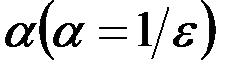 от твердости Нс по [192]
от твердости Нс по [192]

| (3.13) |
где а' — коэффициент пропорциональности; Р — давление в зоне трения.
| Рис.3.7. Зависимость твердости НВ (а) и предела текучести sТ - (б) от температуры t баббита [153] | 
|
Наиболее достоверными показателями теплового режима работы агрегатов в эксплуатации является температура масла в картере или температура охлаждаемой жидкости в двигателе, которую при установившихся режимах можно считать прямо пропорциональной температуре масла в картере. Это обусловлено тем, что масло, смазывая поверхности трения, одновременно и охлаждает их, то есть его температура зависит от температуры поверхности трения. Как показывает анализ многочисленных исследований [1, 3, 10, 34, 43, 93, 106, 148, 151, 153, 166, 172, 204], интенсивность изнашивания изменяется в зависимости от температуры масла в картере нелинейно в отличие от принятой линейной зависимости (3.12) a от температуры поверхности трения и масляной пленки. Следовательно, температура масла в картере агрегатов с температурой поверхности трения связана нелинейно.
Неоднозначность изменения температуры поверхности трения или масляной пленки tП в зависимости от температуры масла в картере агрегата tМ(или температуры окружающего воздуха при постоянном теплообмене) обусловлена различным расходом масла через пары трения. При низкой температуре вследствие высокой вязкости масла его расход через пары трения недостаточен, из-за чего температура масляной пленки и поверхности трения высокая. По мере прогрева масла расход его через пары трения возрастает, что снижает температуру поверхности трения. Дальнейшее повышение температуры масла ведет к пропорциональному увеличению температуры поверхности трения, так как расход масла через пары трения при этом уже стабилизируется.
Аналитически описать зависимость tП от tМ можно с помощью дифференциального уравнения, характеризующего теплообмен между маслом в картере и поверхностью трения при постоянном теплообмене с окружающей средой. При постоянном расходе масла через узел трения tП связана с tМ линейно через коэффициент пропорциональности К. Однако с повышением tМ возрастает расход масла через узел трения, что ведет к снижению tП, которое можно считать пропорциональным вязкости h. С учетом уравнения (3.5) дифференциальное уравнение можно записать в виде
|
|
|

| (3.14) |
где а и b - экспериментальные параметры, характеризующие свойства масла и состояние узла трения.
Интегрирование уравнения (3.14) при начальных условиях tП=tП0 при tМ=0 позволяет получить зависимость tП от tМ в виде

| (3.15) |
С учетом линейной зависимости a от температуры поверхности трения tП (3.12) аналогичная зависимость будет и для a от tМ, то есть

| (3.16) |
где a0 - интенсивность изнашивания при tМ=0; a, b, c - экспериментальные параметры, зависящие от свойств масла, состояния узла трения, скоростного и нагрузочного режимов.
Поскольку функция (3.16) неоднозначная, то можно найти оптимальную температуру масла в картере, при которой наблюдается минимум интенсивности изнашивания, из условия
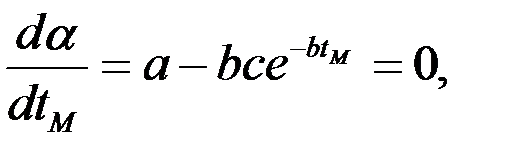 откуда откуда 
| (3.17) |
Поскольку зависимость (3.16) содержит четыре параметра, то требуется приближенное определение двух параметров, а двух других - по методу наименьших квадратов. Для упрощения зависимости (3.16) можно аппроксимировать простым полиномом второго порядка

| (3.18) |
Так как при получении зависимости (3.16) использована линейная зависимость a от tП (3.12) до критической температуры, то уравнение (3.16) также имеет область определения до tMK при которой наступает критическая температура поверхности трения.
Экспериментальные исследования [43] по оригинальным методикам подтверждают полученные зависимости (3.15), (3.16), о чем можно судить по рис. 3.8. На рис. 3.9 – 3.11 приведены зависимости, полученные по результатам обработки данных других исследований.
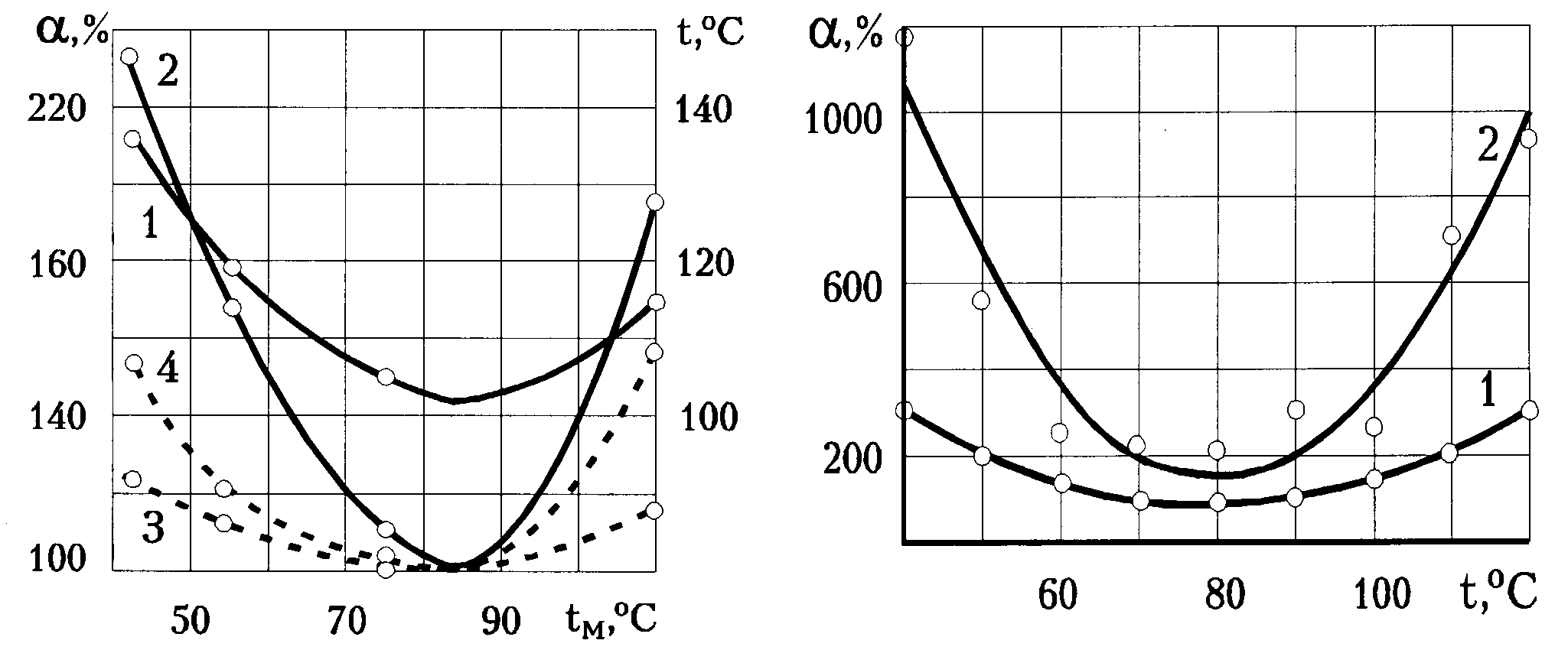
| Рис.3.8. Зависимость температуры t коренных вкладышей (1), интенсивности изнашивания a шатунных (2) и коренных (3) шеек, гильз цилиндров (4) от температуры tМ масла в картере двигателя | Рис.3.9. Зависимость интенсивности изнашивания вкладышей от температуры масла в картере при температуре охлаждающей жидкости, °С: 1 - 70; 2 - 40 (по данным [52]) |

| Рис.3.10. Зависимость интенсивности изнашивания поршневых колец двухтактного дизеля от температуры охлаждающей жидкости [52] | Рис.3.11. Зависимость скорости изнашивания колец от температуры охлаждающей воды: 1 - зимой при температуре воздуха -10 °С (нагрузка 40-65% номинальной); 2 - летом (нагрузка 15% номинальной) [52] |
Дифференцирование уравнения (3.18) позволяет определить оптимальную температуру
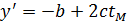 =0.
=0.
Откуда 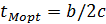 (3.19)
(3.19)
Таким образом, с повышением температуры поверхности трения или масляной пленки в узле трения снижается ее средняя толщина пропорционально вязкостно-температурной характеристике, что ведет к росту взаимодействий микровыступов и интенсивности изнашивания по линейной зависимости (3.9) и (3.10) от h и экспоненциальной (3.11) от tП, которую можно аппроксимировать при tП от 40 до 150°С прямолинейной зависимостью (3.12). После критической температуры интенсивность изнашивания возрастает в несколько раз вследствие малой смазочной способности. Зависимость температуры и интенсивности изнашивания поверхности трения от температуры масла в картере агрегатов (температуры окружающего воздуха) неоднозначная (3.15) и (3.16), что обусловлено зависимостью расхода масла через узел трения от его вязкости. Эти зависимости можно аппроксимировать полиномом второй степени (3.18). Оптимальная температура масла, при которой наступает минимум интенсивности изнашивания, определяется по формуле (3.19).
Для элементов автомобиля, отказы которых носят усталостный характер, влияние температуры сказывается через изменение предела выносливости. При снижении температуры уменьшается пластическая деформация, что способствует повышению предела выносливости [74, 82, 124, 133, 161, 162, 188, 194, 207]. Повышение температуры, способствуя пластической деформации, обусловливает понижение предела выносливости. Однако применительно к элементам автомобиля (рессоры, поворотные кулаки, полуоси и др.) наибольшие колебания температуры наблюдаются в течение года, то есть носят сезонный характер.
Что касается различия в среднегодовой температуре, то для нашей страны оно менее значительно и не превышает 18-20°С. В этих условиях следует учитывать снижение предела выносливости с ростом температуры. Так по данным [161] коэффициент пластичности при изменении температуры от 0 до 15°С возрастает от 12 до 20%, а предел выносливости сталей при этом снижается на 10-15%.
С учетом небольшого снижения предела выносливости при реальных пределах среднегодовой температуры его можно аппроксимировать при этом линейной зависимостью. Об этом свидетельствуют экспериментальные данные [82], приведенные на рис.3.12 с высоким коэффициентом корреляции (r=-0,94), подтверждающие линейную зависимость в виде

| (3.20) |
где s-10 — значение s-1 при t=0 °С(s-10=0,712 для рис.2.22); С - коэффициент пропорциональности (С < 0, для рис.3.12 С=-0,00222).
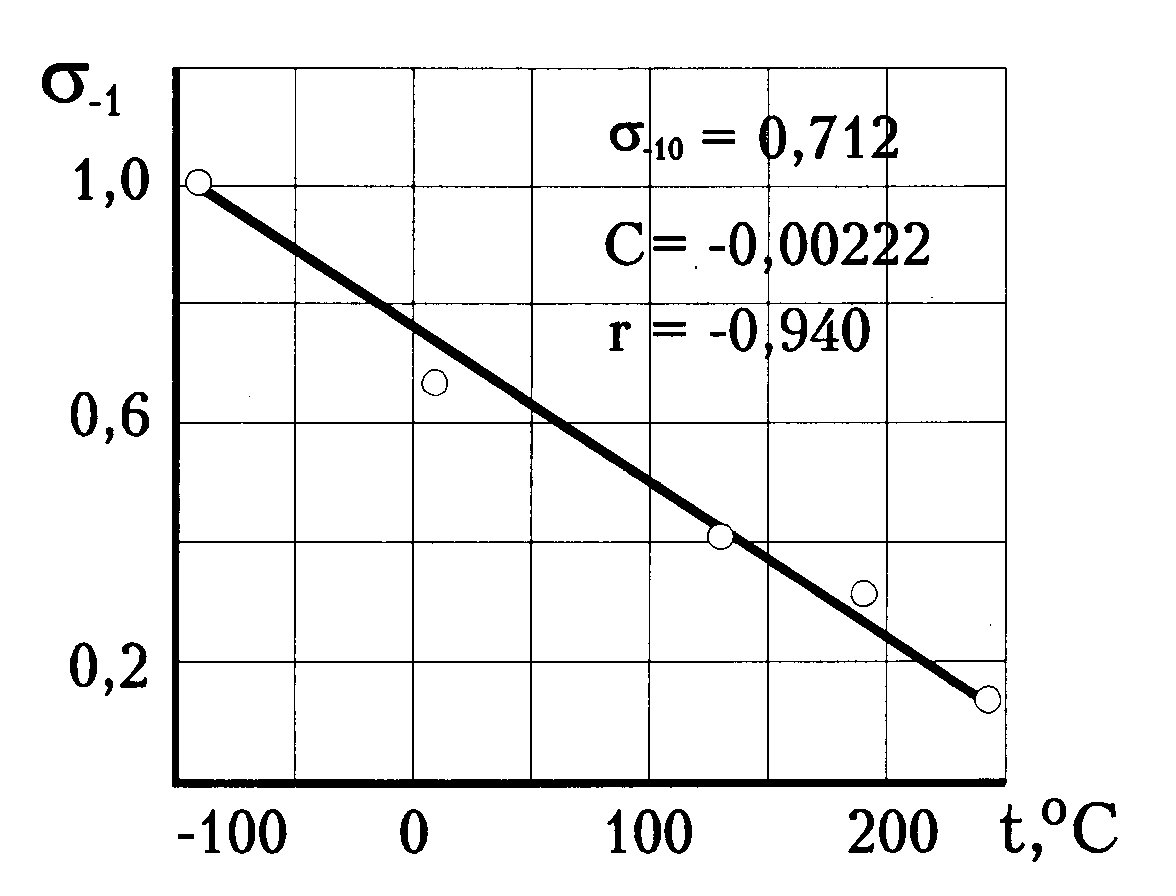
| Рис.3.12. Зависимость относительного изменения предела выносливости образца от температуры (по данным Д.Коллинза [82]) |
С учетом зависимости (2.12) и (3.20) для интенсивности усталостного разрушения aF можно записать
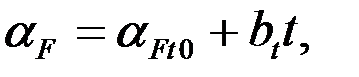
| (3.21) |
где aFt0 - зависимость усталостного разрушения при t=0;bt - коэффициент повышения aF на единицу t.
С учетом зависимостей (2.16) и (2.19) для ресурса этих элементов lK можно записать
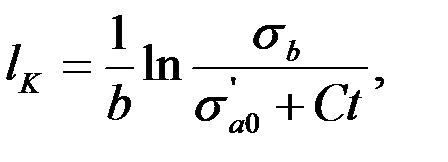
| (3.22) |
где 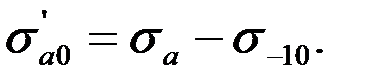
При понижении температуры окружающего воздуха вследствие возрастания предела текучести и снижения пластичности [161] возрастает вероятность хрупкого разрушения деталей. Таким образом, с ростом температуры окружающего воздуха возрастает интенсивность усталостного разрушения (3.21) и снижается ресурс этих элементов (3.22).
|
|
|


