 |
2.3 Теоретические исследования взаимодействия винтовой поверхности шнека смесителя с материалом
|
|
|
|
Рассмотрим вращение винтовой поверхности вокруг её оси в горизонталь- ном смесителе сыпучих материалов, используя теорему об изменении кинетиче- ского момента [84]:
| 𝑑 𝜔 𝐼 = 𝑀 𝑉 𝑅 + � (𝑁 𝑀 𝜑 𝜌 + 𝐹 𝑇 𝑅 𝜑 𝜌 ), 𝑑 𝑡 | (2. 29) |
где 𝐼 - момент инерции вала смесителя вместе с винтовой поверхностью и перемещаемым в переносном движении материалом; 𝜔 - угловая скорость вала;
𝑀 𝑉 𝑅 - вращающий момент со стороны привода, приложенный к валу; 𝑁 𝑀 𝜑 - нор- мальная реакция материала, действующая на элементарную площадку винтовой поверхности в проекции на направление её движения, то есть на цилиндрическую ось 𝑝 ⃗; 𝐹 𝑇 𝑅 𝜑 - сила трения материала, приложенная к элементарной площадке вин- товой поверхности в проекции на ось 𝑝 ⃗; 𝜌 - радиус в цилиндрических координатах элементарной площадки поверхности, который является плечом составляющих сил вдоль направления 𝑝 ⃗. Знак ∑ - означает суммирование моментов от сил, приложенных ко всем элементарным площадкам винтовой поверхности (рис. 2. 7).
| а | б |
Рисунок 2. 7 - Схема взаимодействия винтовой поверхности с материалом в смесителе: а) оси координат и силы; б) элементарная площадка - фрагмент винто-
вой поверхности и скорости движения материала
Для динамического рассмотрения взаимодействия материала и винтовой поверхности сделаем допущения о том, что силы тяжести, приложенные к смеши- ваемому материалу, симметричны относительно вертикального осевого сечения смесителя и не оказывают влияния на вращение шнека. Второе допущение о том, что в процессе взаимодействия элементарного объема материала с элементарной площадкой винтовой поверхности силы трения со стороны других элементарных объемов материала пренебрежимо малы.
|
|
|
При вращении вала смесителя с постоянной угловой скоростью
(𝑑 𝜔 = 0), момент необходимый для её поддержания без учета сопротивления на
𝑑 𝑡
конструкционное трение, определили из выражения (2. 29):
| 𝑀 𝑉 𝑅 = − � (𝑁 𝑀 𝜑 𝜌 + 𝐹 𝑇 𝑅 𝜑 𝜌 ). | (2. 30) |
Нормальная реакция 𝑁 � ⃗ 𝑀 направлена по градиенту к винтовой поверхности.
Уравнение винтовой поверхности в цилиндрических координатах:
| 𝑓 (𝜌, 𝜑, 𝑧 ) = 𝑧 − 𝑎 𝜑 = 0. | (2. 31) |
Вектор градиент к поверхности 𝑓 (𝜌, 𝜑, 𝑧 ) разложили на составляющие по цилиндрическим орт векторам (𝑟 ⃗, � 𝑝 ⃗, � 𝑘 ⃗ ):
| 𝜕 𝑓 1 𝜕 𝑓 𝜕 𝑓 𝑔 𝑟 𝑎 𝑑 (𝑓 ) = 𝑟 ⃗ + 𝑝 ⃗ + 𝑘 � ⃗. 𝜕 𝜌 𝜌 𝜕 𝜑 𝜕 𝑧 | (2. 32) |
Частные производные в выражении (2. 32) равны:
| 𝜕 𝑓 ⎧ = 0; ⎪ 𝜕 𝜌 𝜕 𝑓 = − 𝑎 ; ⎨ 𝜕 𝜑 ⎪ 𝜕 𝑓 = 1. 𝗅 𝜕 𝑧 | (2. 33) |
Тогда градиент к поверхности
| 𝑎 𝑔 𝑟 𝑎 𝑑 (𝑓 ) = − 𝑝 ⃗ + 1 ∙ 𝑘 � ⃗. 𝜌 | (2. 34) |
И его модуль равен
| 𝑎 2 |𝑔 𝑟 𝑎 𝑑 (𝑓 )| = � � � + 1. 𝜌 | (2. 35) |
Нормальная реакция 𝑁 � ⃗ 𝑀 имеет проекции пропорциональные проекциям вектора градиента на оси цилиндрических координат:
| 𝑁 𝑀 𝜌 = 0; 𝑎 � 𝑁 𝑀 𝜑 = − 𝜆 𝜌 ; 𝑁 𝑀 𝑧 = 𝜆 , | (2. 36) |
где 𝜆 - неопределенный множитель Лагранжа.
|
|
|
При использовании правого винта поверхности в соответствии с уравнени- ем (2. 31) и угловой скоростью 𝜔 � ⃗, сонаправленной с осью 𝑧, (рис. 2. 7) этот множи- тель положителен (𝜆 ≥ 0). Величина силы 𝑁 � ⃗ 𝑀 определяет силу трения 𝐹 ⃗ 𝑇 𝑅 по мо- дулю в соответствии с законом Кулона для сухого трения скольжения с коэффи-
циентом 𝑘 𝑇 𝑅:
| ⃗ � ⃗ 𝑎 2 � 𝐹 𝑇 𝑅 � = 𝑘 𝑇 𝑅 � 𝑁 𝑀 � = 𝑘 𝑇 𝑅 𝜆 � � � + 1. 𝜌 | (2. 37) |
Направление силы трения 𝐹 ⃗ 𝑇 𝑅 противоположно относительной скорости элементарного участка поверхности винта по отношению к материалу 𝑣 ⃗ 𝑐. Смеши- ваемый материал до взаимодействия с поверхностью винта находится в состоянии покоя. После взаимодействия - приобретает скорость, имеющую две составляю- щие: переносную � 𝑣 � 𝑒 ⃗, и относительную в движении по винтовой поверхности 𝑣 ⃗ 𝑟, с последней и совпадает по направлению силы трения, приложенной к элементар- ной поверхности.
| 𝐹 ⃗ = 𝑘 � 𝑁 � ⃗ � 𝑣 ⃗ 𝑟 . 𝑇 𝑅 𝑇 𝑅 𝑀 |𝑣 ⃗ 𝑟 | | (2. 38) |
Полагаем, что после взаимодействия с винтовой поверхностью, материал скользит в её касательной плоскости, сохраняя значение относительной состав- ляющей скорости, которое было до взаимодействия (рис. 2. 7). Так как до взаимо- действия материал находился в покое, то относительная скорость 𝑣 ⃗ 𝑟 равна 𝑣 ⃗ 𝑒 𝑐 - проекции скорости элементарной площадки 𝑣 � 𝑒 ⃗ на касательную плоскость к по- верхности, но противоположна ей по направлению (рис. 2. 7, б):
| 𝑣 ⃗ 𝑟 = − 𝑣 ⃗ 𝑒 𝑐. | (2. 39) |
Определим проекцию скорости 𝑣 � 𝑒 ⃗ на направление вектора-градиента:
| 𝑎 � 𝑣 � 𝑒 ⃗ ∙ 𝑔 𝑟 𝑎 𝑑 (𝑓 ) 𝑣 𝑒 ∙ (− 𝜌 ) 𝑣 𝑒 𝑛 = |𝑔 𝑟 𝑎 𝑑 (𝑓 )| = 𝑎 2 . � � � + 1 𝜌 | (2. 40) |
Тогда величина касательной составляющей скорости, находится по теореме Пифагора:
|
|
|
| 𝑣 𝑒 𝑐 = � 𝑣 𝑒 2 − 𝑣 𝑒 𝑛 2 = 𝑣 𝑒 . � 𝑎 2 � � + 1 𝜌 | (2. 41) |
И с учетом равенства (2. 38) модуль относительной скорости 𝑣 𝑟 равен вели- чине 𝑣 𝑒 𝑐:
| 𝑣 𝑟 = 𝑣 𝑒 . � � 𝑎 2 + 1 𝜌 � | (2. 42) |
Найдем проекции скорости элементарной поверхности 𝑣 𝑒 𝑐 на цилиндриче- ские оси координат, учитывая векторное равенство:
| 𝑣 ⃗ 𝑒 𝑐 =𝑣 ⃗ 𝑒 − 𝑣 ⃗ 𝑒 𝑛. | (2. 43) |
Проекции вектора 𝑣 ⃗ 𝑒 в правой части равенства (2. 43) имеют вид
| 𝑣 𝑒 𝜌 = 0; � 𝑣 𝑒 𝜑 = 𝑣 𝑒 = 𝜔 𝜌. 𝑣 𝑒 𝑧 = 0. | (2. 44) |
Проекции нормальной составляющей скорости элементарной поверхности
𝑣 ⃗ 𝑒 𝑛 на оси координат определим с учетом её коллинеарности с вектором градиен- том:
| (𝑔 𝑟 𝑎 𝑑 (𝑓 ))𝜌 𝑣 𝑒 𝑛 𝜌 = 𝑣 ⃗ 𝑒 𝑛 ∙ 𝑟 ⃗ = 𝑣 𝑒 𝑛 |𝑔 𝑟 𝑎 𝑑 (𝑓 )| = 0; | (2. 45) |
| 𝑎 𝑎 𝑎 2 (𝑔 𝑟 𝑎 𝑑 (𝑓 ))𝜑 𝑣 𝑒 ∙ (− 𝜌 ) (− 𝜌 ) 𝑣 𝑒 ∙ (𝜌 ) 𝑣 𝑒 𝑛 𝜑 = 𝑣 ⃗ 𝑒 𝑛 ∙ 𝑝 ⃗ = 𝑣 𝑒 𝑛 |𝑔 𝑟 𝑎 𝑑 (𝑓 )| = 𝑎 2 ∙ 𝑎 2 = 𝑎 2 ; � � � + 1 � � � + 1 � � + 1 𝜌 𝜌 𝜌 | (2. 46) |
| 𝑎 𝑎 (𝑔 𝑟 𝑎 𝑑 (𝑓 ))𝑧 𝑣 𝑒 ∙ (− 𝜌 ) 1 𝑣 𝑒 𝜌 𝑣 𝑒 𝑛 𝑧 = 𝑣 𝑒 𝑛 |𝑔 𝑟 𝑎 𝑑 (𝑓 )| = 𝑎 2 ∙ 𝑎 2 = − 𝑎 2 . � � � + 1 � � � + 1 � � + 1 𝜌 𝜌 𝜌 | (2. 47) |
Тогда, проецируя равенство (2. 43) на цилиндрические оси, получим:
|
|
|
| 𝑣 𝑒 𝑐 𝜌 = 𝑣 𝑒 𝜌 − 𝑣 𝑒 𝑛 𝜌 = 0; | (2. 48) |
| 𝑣 ∙ (𝑎 )2 𝑒 𝜌 1 𝑣 𝑒 𝑐 𝜑 = 𝑣 𝑒 𝜑 − 𝑣 𝑒 𝑛 𝜑 = 𝑣 𝑒 − 𝑎 2 = 𝑣 𝑒 𝑎 2 ; � � + 1 � � + 1 𝜌 𝜌 | (2. 49) |
| 𝑣 ∙ 𝑎 𝑣 ∙ 𝑎 𝑒 𝜌 𝑒 𝜌 𝑣 𝑒 𝑐 𝑧 = 𝑣 𝑒 𝑧 − 𝑣 𝑒 𝑛 𝑧 = 0 − � − 𝑎 2 � = 𝑎 2 . � � + 1 � � + 1 𝜌 𝜌 | (2. 50) |
Учитывая равенство (2. 39), отражающее движение винтовой поверхности в неподвижном изначально материале, найдем проекции относительной скорости 𝑣 ⃗ 𝑟 на оси цилиндрической системы координат:
| 𝑣 𝑟 𝜌 = 0; ⎧ 1 ⎪ 𝑣 𝑟 𝜑 = − 𝑣 𝑒 𝑎 2 ; ⎪ � 𝜌 � + 1 ⎨ 𝑣 ∙ 𝑎 ⎪ 𝑒 𝜌 ⎪ 𝑣 𝑟 𝑧 = − 𝑎 2 . 𝗅 � 𝜌 � + 1 | (2. 51) |
Выражения (2. 51), (2. 42) подставляем в соотношение (2. 38) и находим на- правление силы трения, приложенной к элементарной площадке:
| 𝐹 𝑇 𝑅 𝜌 = 0; ⎧ ⎪ 𝑘 𝑇 𝑅 � 𝑁 � ⃗ 𝑀 � 𝐹 𝑇 𝑅 𝜑 = − ; ⎪ 𝑎 2 � � � + 1 𝜌 ⎨ ⎪ 𝐹 = − 𝑘 𝑇 𝑅 � 𝑁 � ⃗ 𝑀 � . 𝑇 𝑅 𝑧 ⎪ � 𝑎 2 𝗅 � � + 1 𝜌 | (2. 52) |
Зная проекции сил, воздействующих на элементарную площадку поверхно- сти, в правой части выражения (2. 30), на основании (2. 36) и (2. 52) запишем:
| 𝑁 𝑀 𝜑 𝜌 + 𝐹 𝑇 𝑅 𝜑 𝜌 = − 𝜆 𝑎 − 𝑘 𝑇 𝑅 𝜆 𝜌. | (2. 53) |
Множитель 𝜆 равен отношению модуля силы 𝑁 � ⃗ 𝑀 - воздействия материала на площадку 𝑑 𝑆 к модулю 𝑔 𝑟 𝑎 𝑑 (𝑓 ) - вектора-градиента к поверхности:
| � 𝑁 � ⃗ 𝑀 � 𝜆 = . � 𝑎 2 � � + 1 𝜌 | (2. 54) |
С целью определения величины 𝑁 � ⃗ 𝑀 рассмотрим силу 𝑁 � ⃗ 𝐵, с которой элемен- тарная площадка винтовой поверхности воздействует на материал при устано- вившемся движении. По третьему закону Ньютона эти силы равны по величине и противоположны по направлению:
|
|
|
| 𝑁 � ⃗ 𝑀 = − 𝑁 � ⃗ 𝐵. | (2. 55) |
Применим теорему об изменении количества движения к объему материала, который взаимодействует с элементарной площадкой 𝑑 𝑆 за некоторое время 𝑡 в проекции на вектор-градиент к поверхности (рис. 2. 8).
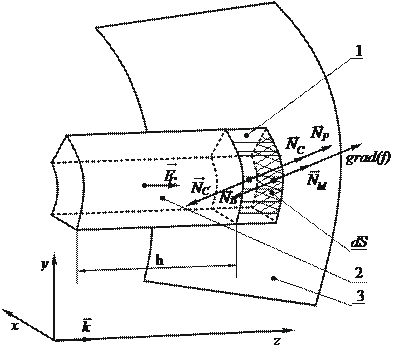
Рисунок 2. 8 - Схема взаимодействия потока разгоняемого материала 1, находящегося в контакте с элементарной площадкой поверхности винта 𝑑 𝑆 и горизонтального слоя 2, в форме косого цилиндра с основанием 𝑑 𝑆 и высотой
равной ℎ - шагу винта (уравновешенные силы тяжести и ответные реакции
не показаны)
С учетом того, что взаимодействующий с поверхностью фрагмент материа- ла не является свободным потоком, на него кроме поверхности винта действуют
соседние фрагменты. Условно их сгруппируем в две составляющие: 𝑁
� 𝑃 ⃗ сила от
давления вышележащих слоев материала и
� 𝐶 ⃗ – сила нормального давления, обу-
словленная сопротивлением горизонтальному перемещению порции материала, заключенной между витками винта и опирающейся на площадку 𝑑 𝑆. Эта порция материала перемещается по горизонтали вдоль оси винта и воздействует на при- легающий к поверхности поток, для которого запишем:
| 𝑡 𝑡 𝑡 𝑄 𝑛 − 𝑄 𝑛 0 = − � 𝑁 𝐵 𝑑 𝑡 + � 𝑁 𝑃 + � 𝑁 𝐶 , 0 0 0 | (2. 56) |
где 𝑄 𝑛 - количество движения, приобретаемое материалом в проекции на направление градиента; 𝑄 𝑛 0 – начальное количество движения материала в про- екции на направление градиента, 𝑄 𝑛 0 = 0, так как материал находился в покое.
В правой части уравнения (2. 56) импульс силы 𝑁 � ⃗ 𝐵 - в проекции на направ- ление градиента к поверхности.
Сила 𝑁
� 𝑃 ⃗ – сила давления верхних слоев материала на объем, взаимодейст-
вующий с элементарной площадкой 𝑑 𝑆. Она определяется по аналогии с давлени- ем в жидкости, но при условии, что движущаяся поверхность обеспечивает на- пряжения сжатия рассматриваемого объема сыпучего материала (то есть, нет дав-
ления с тыльной стороны винтовой поверхности). Сила 𝑁
� 𝑃 ⃗ действует, как сила
статического давления верхних слоев на нижние с допущением равенства по всем направлениям аналогично закону Паскаля для жидкостей:
𝑁 𝑃 = 𝑝 ∙ 𝑑 𝑆 ,
где аналог статического давления 𝑝 определяется через насыпную плот- ность материала 𝛾, ускорение свободного падения 𝑔 и высоту 𝑙, вышележащих слоев над элементарной площадкой:
𝑝 = 𝛾 ∙ 𝑔 (𝜌 к1 − 𝐷 − 𝑦 ),
причем, 𝜌 к1 – максимальный радиус внешнего шнека смесителя; 𝐷 – высота по вертикали незаполненного объема смесителя 𝐷 = 𝜌 к1(1 − 𝑠 𝑖 𝑛 𝜑 0), (рис 2. 9);
𝑦 – вертикальная декартова координата, отсчитываемая от оси винта
𝑦 = 𝜌 ∙ sin 𝜑.
Рисунок 2. 9 - Схема заполнения смесителя и толщина слоя материала 𝑙 до расположения элементарной площадки винтовой поверхности 𝑑 𝑆
Тогда
𝑁 𝑃 = 𝛾 ∙ 𝑔 (𝜌 к1 − 𝐷 − 𝜌 ∙ sin 𝜑 )𝑑 𝑆.
В выражении (2. 55) сила
� 𝑁
� 𝐶 ⃗ – это сила, преодолевающая силу трения
� 𝐹 � 𝐶 ⃗
(вдоль оси z), при горизонтальном перемещении материала, заключенного между витками шнека, длиной равной шагу винта ℎ,
|
𝐹 𝐶 = 𝑔 ∙ 𝛾 ∙ 𝑑 𝑆 ∙ cos � 𝑔 𝑟 𝑎 𝑑
𝑓 )𝑘 � ⃗ � ∙ ℎ ∙ 𝑘 𝑐 ,
где 𝑘 𝑐 – коэффициент трения между слоями материала;
|
𝑑 𝑆 ∙ cos � 𝑔 𝑟 𝑎 𝑑
𝑓 )𝑘 � ⃗ � – проекция площадки 𝑑 𝑆 на плоскость (𝑥, 𝑦 ).
Суммарная сила трения материала, перемещаемого винтовой поверхностью вдоль горизонтальной оси 𝑧 равна
� 𝐹 𝐶 = �
(𝑆 )
�
|
𝑓 )𝑘 � ⃗ � ∙ ℎ ∙ 𝑘 𝑐
𝑑 𝑆.
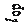
Но эта сила распределена по вертикали неравномерно, так как нижние слои находятся под давлением верхних. Примем допущение о том, что сила трения при горизонтальном перемещении вдоль оси 𝑧 прямо пропорциональна глубине слоя по оси 𝑦, обозначим ее 𝑙
𝑙 = (𝜌 к1 − 𝐷 − 𝑦 ),
тогда сила трения, относящаяся к элементарной площадке 𝑑 𝑆 равна
|
𝐹 𝐶 = 𝑔 ∙ 𝛾 ∙ 𝑑 𝑆 ∙ cos � 𝑔 𝑟 𝑎 𝑑
𝑓 )𝑘 � ⃗ � ∙ ℎ ∙ 𝑘 𝑐 𝑙
𝑙
,
𝑐 𝑝
где 𝑙 𝑐 𝑝 – усредненная глубина слоя материала по поверхности винта S:
𝑙 𝑐 𝑝 =
∬ (𝑆 ) 𝑙 𝑑 𝑆
∬ (𝑆 ) 𝑑 𝑆
∬ (𝑆 )(𝜌 к1 − 𝐷 − 𝑦 )𝑑 𝑆
= ,
𝑆
где 𝑙 𝑐 𝑝 - является величиной постоянной при стационарном движении и оп- ределяется как отношение интегралов по поверхности первого рода:
∫ 𝜑 𝑘 (∫ 𝜌 к
(𝜌 − 𝐷 − 𝜌 ∙ sin 𝜑 )� 𝑎 2 + 𝜌 2 𝑑 𝜌 )𝑑 𝜑
𝑙 𝑐 𝑝 =
𝜑 0 𝜌 0
к1
∫ 𝜑 𝑘 (∫ 𝜌 к � 𝑎 2 + 𝜌 2 𝑑 𝜌 )𝑑 𝜑 .
𝜑 0 𝜌 0
Соотношение между силой трения
� 𝐹 � 𝐶 ⃗ и силой дополнительного нормально-
го давления
� 𝑁
� 𝐶 ⃗ на элементарный объем, взаимодействующий с поверхностью
|
противоположна по знаку работе силы
� 𝐹 � 𝐶 ⃗ на том же перемещении (на рис. 2. 8 ма-
териал перемещается противоположно оси 𝑧 ):
|
− 𝑁 ′ 𝐶 ∙ 𝛿 𝑧 ∙ cos � 𝑔 𝑟 𝑎 𝑑
𝑓 )𝑘 � ⃗ � + 𝐹 𝐶 ∙ 𝛿 𝑧 = 0.
|
� 𝑁
� 𝐶 ⃗ по закону равенства действия и противо-
действия
|
� 𝐶 ⃗,
где
�
|
𝑓 )𝑘 � ⃗ � =
√ � 𝑎 � 2+1
– косинус угла между градиентом к поверхно-
𝜌
сти и осью 𝑧. Тогда
𝑁 𝐶
= 𝐹 𝐶
|
cos � 𝑔 𝑟 𝑎 𝑑
𝑓 )𝑘 � ⃗ �
= 𝛾 ∙ 𝑑 𝑆 ∙ ℎ ∙ 𝑘
𝑙
𝑐 𝑙 𝑐 𝑝
= 𝑔 ∙ 𝛾 ∙ 𝑑 𝑆 ∙ ℎ ∙ 𝑘 𝑐
(𝜌 к1 − 𝐷 − 𝑦 ).
𝑙 𝑐 𝑝
Подставляя выражение для 𝑦 получим:
𝑁 𝐶
= 𝑔 ∙ 𝛾 ∙ ℎ ∙ 𝑘 𝑐
(𝜌 к1 − 𝐷 − 𝜌 ∙ sin 𝜑 ) ∙ 𝑑 𝑆.
𝑙 𝑐 𝑝
После взаимодействия с поверхностью материал приобретает скорость 𝑣 ⃗, которая складывается из переносной 𝑣 ⃗ 𝑒 и относительной 𝑣 ⃗ 𝑟 составляющих, про- екции которых на оси координат определены ранее по выражениям (2. 44) и (2. 51) соответственно. Относительная скорость 𝑣 ⃗ 𝑟 не имеет проекции на вектор- градиент, а переносная скорость 𝑣 ⃗ 𝑒 имеет проекцию на направление градиента по соотношению (2. 40), тогда
| 𝑣 ∙ (− 𝑎 ) 𝑒 𝜌 𝑄 𝑛 = 𝑚 ∙ , √ � 𝑎 2 + 1 𝜌 � | (2. 57) |
где 𝑚 - масса материала, взаимодействующая с элементарной площадкой за время 𝑡. При установившемся движении, кода винтовая поверхность погружена в материал, величина 𝑚 определяется выражением:
| 𝑚 = 𝛾 ∙ 𝑣 𝑒 ∙ 𝑡 ∙ 𝑑 𝑆 ∙ cos(𝛼 ), | (2. 58) |
где 𝛾 - насыпная плотность материала; 𝛼 – угол между направлением дви- жения площадки 𝑑 𝑆 и направлением, противоположным вектору-градиенту этой площадки. Направление противоположно, потому что винт взаимодействует с ма-
териалом (рис. 2. 9) стороной противоположной направлению 𝑔 𝑟 𝑎 𝑑 (𝑓 ).
| 𝑎 (− 𝑔 𝑟 𝑎 𝑑 (𝑓 )) 𝜌 cos(𝛼 ) = 𝑝 ⃗ ∙ |𝑔 𝑟 𝑎 𝑑 (𝑓 )| = 𝑎 2 . √ ( ) + 1 𝜌 | (2. 59) |
Тогда, после подстановки (2. 59) в (2. 58) и (2. 58) в (2. 57), получим:
| 𝑎 2 ( ) 𝑄 = − 𝛾 ∙ 𝑣 2 ∙ 𝑡 ∙ 𝑑 𝑆 𝜌 . 𝑛 𝑒 𝑎 2 (𝜌 ) + 1 | (2. 60) |
Составляя теорему об изменении количества движения (2. 56) при устано- вившемся движении, запишем:
| (𝑎 2 𝜌 ) − 𝛾 ∙ 𝑣 𝑒 2 ∙ 𝑡 ∙ 𝑑 𝑆 2 − 0 = − 𝑁 𝐵 ∙ 𝑡 + 𝑁 𝑃 ∙ 𝑡 + 𝑁 𝐶 ∙ 𝑡. 𝑎 ( ) + 1 𝜌 | (2. 61) |
Откуда определяем величину силы воздействия элементарной площадки 𝑑 𝑆
на материал
| 𝑎 2 ( ) 𝑁 = 𝛾 ∙ 𝑣 2 ∙ 𝑑 𝑆 𝜌 + 𝛾 ∙ 𝑔 (𝜌 − 𝐷 − 𝜌 ∙ sin 𝜑 )𝑑 𝑆 + 𝐵 𝑒 𝑎 2 к1 (𝜌 ) + 1 (𝜌 к1 − 𝐷 − 𝜌 ∙ sin 𝜑 ) +𝑔 ∙ 𝛾 ∙ ℎ ∙ 𝑘 𝑐 𝑙 ∙ 𝑑 𝑆. 𝑐 𝑝 | (2. 62) |
С учетом равенств (2. 62) и (2. 55) имеем соотношение для алгебраической величины силы воздействия материала на площадку 𝑑 𝑆
| 𝑎 2 ( ) 𝑁 = 𝑁 = 𝛾 ∙ 𝑣 2 ∙ 𝑑 𝑆 𝜌 + 𝛾 ∙ 𝑔 (𝜌 − 𝐷 − 𝜌 ∙ sin 𝜑 )𝑑 𝑆 + 𝑀 𝐵 𝑒 𝑎 2 к1 (𝜌 ) + 1 (𝜌 к1 − 𝐷 − 𝜌 ∙ sin 𝜑 ) +𝑔 ∙ 𝛾 ∙ ℎ ∙ 𝑘 𝑐 𝑙 ∙ 𝑑 𝑆. 𝑐 𝑝 | (2. 63) |
Из-за громоздкости выражения (2. 63) множитель 𝜆, который является коэф- фициентом пропорциональности между вектором-градиентом 𝑔 𝑟 𝑎 𝑑 (𝑓 ) и силой
𝑁 � ⃗ 𝑀 разобьем на три составляющие в соответствии со слагаемыми в выражении (2. 63), обозначив:
𝑎 2
( )
𝛾 ∙ 𝑣 2 ∙ 𝑑 𝑆 𝜌
𝑒 𝑎 2
(𝜌 ) + 1
𝜆 𝑄 =
|𝑔 𝑟 𝑎 𝑑 (𝑓 )| ;
𝜆 𝑝 =
𝛾 ∙ 𝑔 (𝜌 к1 − 𝐷 − 𝜌 ∙ sin 𝜑 )𝑑 𝑆
|𝑔 𝑟 𝑎 𝑑 (𝑓 )| ;
𝜆 𝑐 =
𝛾 ∙ ℎ ∙ 𝑘 𝑐
(𝜌 к1 − 𝐷 − 𝜌 ∙ sin 𝜑 ) ∙ 𝑑 𝑆
𝑙 𝑐 𝑝
|𝑔 𝑟 𝑎 𝑑 (𝑓 )| ;
𝜆 = 𝜆 𝑄 + 𝜆 𝑝 + 𝜆 𝑐.
Первое слагаемое 𝜆 𝑄 на основании выражения дает
| 𝑎 2 ( ) 𝜆 = 𝛾 ∙ 𝑣 2 ∙ 𝑑 𝑆 𝜌 𝑄 𝑒 3. � 𝑎 )2 + 1 2 ( � 𝜌 | (2. 64) |
Используя множитель 𝜆 𝑄 в равенстве (2. 53) получим
| 𝑎 2 ( ) (𝑎 + 𝑘 𝑇 𝑅 𝜌 ) � 𝑁 𝜌 + 𝐹 𝜌 � = − 𝛾 ∙ 𝑣 2 ∙ 𝑑 𝑆 𝜌 = 𝑀 𝜑 𝑇 𝑅 𝜑 𝑄 𝑒 3 � 𝑎 2 + 1� 2 ( ) 𝜌 𝑎 2(𝑎 + 𝑘 𝑇 𝑅 𝜌 ) = − 𝛾 ∙ 𝜔 2 ∙ 𝑑 𝑆 3 . � (𝑎 2 + 1 2 𝜌 ) � | (2. 65) |
И, подставляя результат (2. 65) в выражение (2. 30) найдем вращающий мо- мент, необходимый для воздействия на материал при заданной угловой скорости
𝜔:
| 𝑎 2(𝑎 + 𝑘 𝑇 𝑅 𝜌 ) 𝑀 𝑉 𝑅 𝑄 = � 𝛾 ∙ 𝜔 2 ∙ 3 𝑑 𝑆. � (𝑎 2 + 1 2 𝜌 ) � | (2. 66) |
Переходя от дискретного суммирования к непрерывному, получим интеграл по винтовой поверхности первого рода
| 𝑎 2(𝑎 + 𝑘 𝑇 𝑅 𝜌 ) 𝑀 𝑉 𝑅 𝑄 = � 𝛾 ∙ 𝜔 2 ∙ 3 𝑑 𝑆. (𝑆 ) � 𝑎 2 + 1� 2 ( ) 𝜌 | (2. 67) |
Учитывая, что площадь элементарной площадки равна
| 𝑑 𝑆 = � 𝑎 2 + 𝜌 2𝑑 𝜌 𝑑 𝜑, | (2. 68) |
разобьём интеграл по поверхности на двойной кратный интеграл по двум цилиндрическим координатам
| 𝜑 𝑘 𝜌 к 𝑎 2(𝑎 + 𝑘 𝑇 𝑅 𝜌 ) 𝑀 𝑉 𝑅 𝑄 = � (� 𝛾 ∙ 𝜔 2 ∙ 3 � 𝑎 2 + 𝜌 2 𝑑 𝜌 )𝑑 𝜑, 𝜑 0 𝜌 0 � 𝑎 2 + 1� 2 ( ) 𝜌 | (2. 69) |
где: 𝜑 0, 𝜑 𝑘 – начальное и конечное значение полярного угла;
𝜌 0, 𝜌 𝑘 - начальное и конечное значение радиуса.
 |
Сокращая числитель и знаменатель (2. 69) на � 𝑎 2 + 𝜌 2, получим
| 𝜑 𝑘 𝜌 к 𝑎 2(𝑎 + 𝑘 𝑇 𝑅 𝜌 ) 𝑀 𝑉 𝑅 𝑄 = � (� 𝛾 ∙ 𝜔 2 ∙ 𝜌 3 𝑑 𝜌 )𝑑 𝜑. 𝜑 𝜌 (𝑎 2 + 𝜌 2) 0 0 | (2. 70) |
Интеграл (2. 70) имеет громоздкое аналитическое выражение, поэтому вы- числения проводились в программе «Mathcad» с использованием символьного
процессора и последующей подстановкой числовых значений всех величин.
Аналогично на основании второго слагаемого в выражении (2. 63) запишем:
𝜆 𝑃 = 𝛾 ∙ 𝑔 (𝜌 к1 − 𝐷 − 𝜌 ∙ sin 𝜑 ) 𝑑 𝑆,
𝑎 2
√ ( ) + 1
𝜌
� 𝑁
𝜌 + 𝐹 𝜌 �
= (− 𝑎 − 𝑘
𝜌 ) 𝛾 ∙ 𝑔 (𝜌 к1 − 𝐷 − 𝜌 ∙ sin 𝜑 )𝑑 𝑆.
𝑀 𝜑
𝑇 𝑅 𝜑 𝑃
𝑇 𝑅
𝑎 2
|
𝜌
Используя уравнение (2. 30) получим:
𝛾 ∙ 𝑔 (𝜌 к1 − 𝐷 − 𝜌 ∙ sin 𝜑 )𝑑 𝑆
𝑀 𝑉 𝑅 𝑃 = � (𝑎 + 𝑘 𝑇 𝑅 𝜌 ) .
(𝑆 )
𝑎 2
√ ( ) + 1
𝜌
Учитывая, что площадь элементарной площадки равна
 |
𝑑 𝑆 = � 𝑎 2 + 𝜌 2𝑑 𝜌 𝑑 𝜑, интеграл по поверхности примет вид
| 𝜑 𝑘 𝜌 к 𝛾 ∙ 𝑔 (𝜌 к1 − 𝐷 − 𝜌 ∙ sin 𝜑 ) 𝑀 𝑉 𝑅 𝑃 = � (� (𝑎 + 𝑘 𝑇 𝑅 𝜌 ) � 𝑎 2 + 𝜌 2 𝑑 𝜌 )𝑑 𝜑. 𝜑 0 𝜌 0 √ 𝑎 2 ( ) + 1 𝜌 | (2. 71) |
Также определим вклад во вращающий момент третьего слагаемого в вы- ражении (2. 63):
(𝑁 𝑀 𝜑 𝜌 + 𝐹 𝑇 𝑅 𝜑 𝜌 )𝐶 = − 𝜆 𝑐 𝑎 − 𝑘 𝑇 𝑅 𝜆 𝑐 =
= (− 𝑎 − 𝑘 𝑇 𝑅 𝜌 )
𝑔 ∙ 𝛾 ∙ ℎ ∙ 𝑘 𝑐
(𝜌 к1 − 𝐷 − 𝜌 ∙ sin 𝜑 ) ∙ 𝑑 𝑆
𝑙 𝑐 𝑝
|𝑔 𝑟 𝑎 𝑑 (𝑓 )| ;
𝑔 ∙ 𝛾 ∙ ℎ ∙ 𝑘 𝑐
(𝜌 к1 − 𝐷 − 𝜌 ∙ sin 𝜑 ) ∙ 𝑑 𝑆
𝑙 𝑐 𝑝
(𝑁 𝑀 𝜑 𝜌 + 𝐹 𝑇 𝑅 𝜑 𝜌 )𝐶 = (− 𝑎 − 𝑘 𝑇 𝑅 𝜌 ) .
𝑎 2
√ ( ) + 1
𝜌
При суммировании в уравнение (2. 30) данная составляющая будет пред- ставлена интегралом по координатам 𝜑 и 𝜌
| 𝜑 𝜌 𝑔 ∙ 𝛾 ∙ ℎ ∙ 𝑘 (𝜌 к1 − 𝐷 − 𝜌 ∙ sin 𝜑 ) 𝑘 𝑘 𝑐 𝑙 𝑐 𝑝 𝑀 𝑉 𝑅 𝐶 = � (� (𝑎 + 𝑘 𝑇 𝑅 𝜌 ) � 𝑎 2 + 𝜌 2𝑑 𝜌 )𝑑 𝜑. 𝜑 0 𝜌 0 √ 𝑎 2 ( ) + 1 𝜌 | (2. 72) |
Учитывая, что границы 𝜌 и 𝜑 в каждом из интегралов не завися
|
|
|
