 |
Одноканальная система с отказами.
|
|
|
|
Использование теории массового обслуживания при организации сервиса машин
Элементы теории массового обслуживания
Теория массового обслуживания (ТМО) количественно описывает совокупность однородных случайных событий, которые происходят в реальных условиях.
В 1919 г. датский математик Эрланг впервые математически описал нагрузку телефонных станций. Затем теория массового обслуживания нашла мировое применение в различных областях техники, в том числе на автомобильном транспорте.
Теория массового обслуживания описывает так называемые марковские случайные процессы, называемые в честь известного русского ученого А.А. Маркова. Случайный процесс называется марковским в том случае, если вероятность будущего состояния системы, отвечающей данному процессу, зависит только от ее состояния в настоящий момент времени и не зависит от того, в каких состояниях она была в прошлом.
Системы массового обслуживания (СМО) - это системы, в которые в случайные моменты времени поступают требования (заявки) на обслуживание, при этом поступившие требования обслуживаются с помощью имеющихся в системе каналов (постов) обслуживания.
В качестве критериев эффективности работы системы массового обслуживания, в зависимости в зависимости от характера решаемой задачи, могут быть:
· вероятность немедленного обслуживания заявки;
· вероятность отказа в обслуживании;
· среднее число обслуженных заявок и заявок, получивших отказ;
· среднее время ожидания обслуживания; средняя длина очереди; относительная и абсолютная пропускная способность системы;
· убытки от простоя заявок в очереди и незанятых каналов обслуживания и другие.
|
|
|
Виды систем массового обслуживания
Различают два основных вида систем массового обслуживания:
1. Системы с отказами, в которых заявка, поступившая в систему в момент, когда все каналы заняты, получает отказ и покидает систему;
2. Системы с ожиданием (очередью), в которых заявка, поступившая в момент, когда все каналы обслуживания заняты, становится в очередь и ждет, пока не освободится один из каналов.
СМО с ожиданием делятся на системы с ограниченным ожиданием и с неограниченным ожиданием. Ожидание ограничивается или длиной очереди, или временем пребывания в очереди. В системах с неограниченным ожиданием заявка, стоящая в очереди ждет обслуживания неограниченно долго, пока не дойдет очередь. Примером такой системы является зона текущего ремонта автомобилей в АТП.
Одноканальная система с отказами.
Рассмотрим простейший случай, когда СМО имеет в своем распоряжении всего один канал обслуживания (п =1) и работает с отказами. Состояние данной системы можно изобразить графически в виде графа состояний: где х0 - состояние системы, когда канал не занят; х1 - состояние системы, когда канал занят; Р - вероятности перехода системы из одного состояния в другое (Р00 вероятность того, что за время ∆t не поступит ни одной заявки; Р10 - вероятность того, что за время ∆t заявка будет обслужена; P01 - вероятность того, что за время ∆t поступит заявка; Р11 - вероятность того, что за время ∆t заявка не обслужится).
| Р01 |
| х1 |
| х0 |
| Р11 |
| Р00 |
| Р10 |
| х0 |
| х1 |
Рис. 5.1. Граф состояний одноканальной СМО с отказами
Многочисленными наблюдениями за СМО установлено, что число требований (заявок), поступающих в канал обслуживания, распределено по закону Пуассона
 , (5.1)
, (5.1)
где Р(к) - вероятность того, что за время ∆t поступит к заявок (к = 0,1,2,…); λ - плотность или интенсивность заявок, то есть среднее число заявок в единицу времени; ∆t - отрезок времени, за который рассматривается вероятность поступления заявок;
|
|
|
Вероятность того, что за время ∆t не поступит ни одной заявки (к = 0) составит
 . (5.2)
. (5.2)
Многочисленными наблюдениями за СМО установлено также, что время обслуживания одной заявки распределено по показательному закону, плотность которого
 , (5.3)
, (5.3)
где μ - интенсивность обслуживания, то есть среднее число обслуживаний в единицу времени μ = 1/Мt об; Мt об - среднее время обслуживания заявки.
Вероятность того, что за время ∆t заявка будет обслужена, составит
 . (5.4)
. (5.4)
При этом вероятность того, что за время ∆t заявка не будет обслужена, составит
 . (5.5)
. (5.5)
Сравнивая выражения (5.2) и (5.5) видим, что время между двумя заявками распределено по показательному закону. Это позволяет моделировать случайные моменты времени поступления заявок на обслуживание.
Выражения (5.2) и (5.4) могут быть преобразованы с использованием разложения в ряд Маклорена
 . (5.6)
. (5.6)
Отбрасывая члены ряда второго порядка и выше для выражений (5.2) и (5.4) запишем
 ; (5.7)
; (5.7)
 (5.8)
(5.8)
Канал может быть в состоянии х0 в двух случаях:
1. в момент t система находилась в состоянии х0, а за время Δ t не пришло ни одной заявки;
2. в момент t система находилась в состоянии х1, а за время ∆t канал освободился и система перешла в состояние х0.
Вероятность того, что в момент времени (t+ ∆ t) система будет находиться в х0 состоянии по теореме сложения вероятностей равна сумме вероятности двух указанных выше случаев
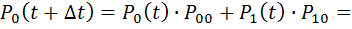
 (5.9)
(5.9)
Вероятность указанных выше событий (1 и 2) равна произведению вероятностей событий в них входящих.
Раскрывая скобки и группируя переменные, получаем
 . (5.10)
. (5.10)
Аналогично и для 
 (5.11)
(5.11)
Уравнения (5.10) и (5.11) называются разностными. Переходя к пределу при ∆ t→ 0, получаем систему дифференциальных уравнений Эрланга
 , (5.12)
, (5.12)
 . (5.13)
. (5.13)
Приведенная система дифференциальных уравнений Эрланга является частным случаем системы дифференциальных уравнений Колмогорова.
Для установившегося режима (λ = const) производные равны нулю, поэтому система дифференциальных уравнений (5.12) и (5.13) преобразуется в систему алгебраических уравнений, в частности для одноканальной системы с отказами получим
|
|
|
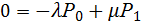 , откуда
, откуда  . (5.14)
. (5.14)
Рассматривая выражение (5.14), формулируем следующее важное мнемоническое правило: «Что вытекает, то и втекает». Для каждого состояния сумма членов, соответствующая выходящим стрелкам, равна сумме членов, соответствующих входящим. Каждый член равен интенсивности потока событий, переводящих систему по данной стрелке, умноженной на вероятность того состояния, из которого выходит стрелка.
Применительно к одноканальной системе с отказами это значит, что ее перевод слева направо осуществляется с плотностью λ, а обратный перевод справа налево - с плотностью μ.
Мнемоническое правило остается справедливым и для многоканальной системы с отказами и с ожиданием в очереди.
Из равенства (5.14) с учетом того, что Р0 + Р1 = 1, получаем
 , откуда
, откуда
 , (5.15)
, (5.15)
при этом  , (5.16)
, (5.16)
где α= λ/μ - приведенная плотность или загрузка системы.
Пример: Исследуется работа СТОА с отказами. Станция имеет один подъемник (канал, п = 1). На станцию поступает простейший пуассоновский поток заявок с плотностью λ = 5 автомобилей в час. Время обслуживания распределено по показательному закону и характеризуется средней продолжительностью Мt об = 0,333 ч на автомобиль. Определить показатели эффективности станции за 10 - часовой рабочий день.
Решение:
1. Плотность или интенсивность обслуживания μ = 1/ Мt об= 1/0,333 = 3 автомобиля в ч.
2. Определяем вероятность того, что машина будет принята для немедленного обслуживания. Эта вероятность называется относительной пропускной способностью СМО
 = 0,375
= 0,375
Следовательно, 37,5% прибывающих автомобилей будет поставлено на немедленное обслуживание.
3. Находим абсолютную пропускную способность станции
 λ∙ Р0 = 5∙0,375 = 1,875 авт. в ч,
λ∙ Р0 = 5∙0,375 = 1,875 авт. в ч,
а за десять ч 18,75 автомобиля.
4. Определим вероятность отказа
Ротк = 1- Р0 = 1 - 0,375 = 0,625.
Следовательно, 62,5% прибывающих автомобилей получают отказ.
5. Находим номинальную или максимально возможную пропускную способность за 10 часовой рабочий день
 = 3 · 10 = 30 автомобиля в день.
= 3 · 10 = 30 автомобиля в день.
|
|
|
Как видим, абсолютная пропускная способность примерно в 1,5 раза меньше номинальной. Это расхождение объясняется случайным характером потока заявок и случайным временем обслуживания заявок.
|
|
|


