 |
Многоканальная система массового обслуживания с отказами
|
|
|
|
Допустим, что система имеет п каналов и работает с отказом. Строим граф состояний (рис. 5.2)
Из графа состояний видно, что перевод системы слева направо осуществляется с плотностью λ, что обусловлено независимостью потока заявок от числа каналов обслуживания. Обратный перевоз системы справа налево осуществляется с суммированной плотностью кμ (суммируются потоки от всех занятых каналов).
| х2 к=2 |
| х0 к=0 |
| х1 к=1 |
| хк к=к |
| хп к=п |
| λ |
| λ |
| λ |
| λ |
…… ……
| пμ |
| μ |
| 2μ |
| кμ |
где к - число занятых каналов.
Рис. 5.2. Граф состояний многоканальной СМО с отказами
Применяя мнемоническое правило «что вытекает, то и втекает» получаем:
для к=0: Р0 = μР1; Р1=  Р0 = λ Р0 : Р0 =
Р0 = λ Р0 : Р0 = 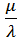 Р1
Р1
для к=1: λ Р1 + μР1 = λ Р0 +2 μР2; 2 μР2= λ Р1 + μР1 - λ Р0
2 μР2= λ Р1 + μР1 - λ  Р1; Р2 =
Р1; Р2 =  Р1=
Р1=  Р1=
Р1= 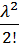 Р0
Р0
для к=2: λ Р2+2 μР2 = λ Р1 +3 μР3; 3 μР3 = λ Р2 +2 μР2 - λ Р1;
3 μР3 = λ Р2+ μР2 - λ  Р2; Р3 =
Р2; Р3 =  Р2 =
Р2 =  Р2 =
Р2 = 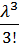 Р0
Р0
Аналогично и для к и п занятых каналов. В общем случае можно записать
| Число занятых каналов | Приведенное правило «что вытекает, то и втекает» | Вероятности состояний для многоканальной системы с отказами |
| к=0 | λ Р0 = μР1 | Р1= 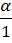 Р0 Р0
|
| к=1 | λ Р1 = 2μР2 | Р2=  Р1 = Р1 = 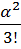 Р0 Р0
|
| к=2 : : к - 1 : : п - 1 | λ Р2 = 3μР3 : : λ Рк-1 = кμРк : : λ Рп-1 = пμРп | Р3 = 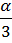 Р2 = Р2 =  Р0
:
:
Рк = Р0
:
:
Рк =  Рк-1 = Рк-1 = 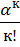 Р0
:
:
Рп = Р0
:
:
Рп =  Рn-1 = Рn-1 = 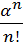 Р0 Р0
|
Сумма вероятностей всех состояний должна быть = 1 потому
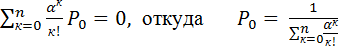 . (5.17)
. (5.17)
Пример: смотри условие предыдущего примера, только п = 2 (λ = 5; μ = 3; п = 2).
Решение:
1. Определяем параметр α, то есть приведенную плотность
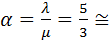 1,67
1,67
2. Определим вероятность состояния х0, то есть полного простоя станции
|
|
|
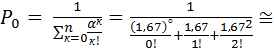 0,246
0,246
Следовательно, 24,6% времени станция будет полностью простаивать (в предыдущем примере Р0 = 0,375)
3. Определим вероятность других состояний
Р1 = α Р0= 1,67·0,246 = 0,41;  0,344
0,344
Проверка
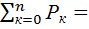 0,246 + 0,41 + 0,344 =1 (верно)
0,246 + 0,41 + 0,344 =1 (верно)
4. Вероятность отказа системы
Ротк= Р2 =0,344
То есть, 34,4% получают отказ (в предыдущем примере Ротк =0,625)
5. Относительная пропускная способность
qотн = 1- Ротк = 1 - 0,344 = 0,656
То есть, 65,5% автомобилей будут обслужены (в предыдущем примере 37,5%)
6. Определяем абсолютную пропускную способность станции:
за 1 ч → Qабс = λ · qотн = 5 · 0,656 = 3,28 авт./час
за 10 ч → 32,8 авт. (в предыдущем примере ≈ 19 авт.)
7. Определяем номинальную (max) пропускную способность станции
Qmax = μ·t·n = 3·10·2 = 60 авт.
8. Отношение 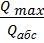 =
=  = 1,83 (в предыдущем примере -1,6)
= 1,83 (в предыдущем примере -1,6)
9. Определим среднее число занятых каналов
М(к) = 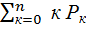 = 1 · 0,41 + 2 · 0,344 = 1,098 каналов.
= 1 · 0,41 + 2 · 0,344 = 1,098 каналов.
Многоканальные СМО с ожиданием при
Ограниченной очереди
Допустим СМО имеет п каналов обслуживания и m мест в очереди. Как только все места в очереди заняты заявка получает отказ. Построим граф состояний (рис.5.3)
| х2 к=2 |
| х 0 к=0 |
| х1 к=1 |
| пμ |
| хп к=п |
| λ |
| λ |
| λ |
| λ |
| 2μ |
| кμ |
| μ |
| xn+3 S=3 |
| xn+2 S=2 |
| xn+m S=m |
| λ |
| λ |
| λ |
| пμ |
| пμ |
| пμ |
| хп+1 S=п |
….. …..
| Нет очереди |
| Возникает очередь |
Рис. 5.3. Граф состояний многоканальной СМО с ожиданием при ограничении очереди
Из графа состояний видно, что поток слева направо характеризуется плотностью λ, а справа налево до возникновения очереди суммарной плотностью кμ, а после возникновения очереди постоянной плотностью пμ.
Пользуясь мнемоническим правилом вычислим вероятности состояний системы:
До возникновения очереди
| Число занятых каналов, к | Приведенное правило «что втекает, то и вытекает» | Вероятности состояний системы |
| : : к=п- 1 | λ Р0 = μР1 λ Р1 = 2μР2 λ Р2 = 3μР3 : : λ Рк-1 = кμРк | Р1= α Р0
Р2= 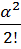 Р0
Р3 = Р0
Р3 =  Р0
:
:
Рп = Р0
:
:
Рп = 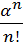 Р0 Р0
|
|
|
|
После возникновения очереди
| Число занятых мест S, | Приведенное правило «что втекает, то и вытекает» | Вероятности состояний системы |
| : : S : : m | λ Рn = nμРn+1 λ Рn+1 = nμРn+2 λ Рn+2 = nμРn+3 : : λ Рn+S-1 = nμРn+3 : : λ Рn+m-1 = nμРn+m | Рn+1 = 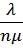 Рn = Рn = 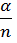 · · 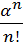 Р0
Рn+2 = Р0
Рn+2 = 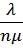 Рn+1 = Рn+1 =  · · 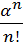 Р0
Рn+3 = Р0
Рn+3 = 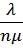 Рn+2 = Рn+2 = 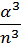 · · 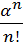 Р0
:
:
Рn+3 = Р0
:
:
Рn+3 = 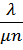 Рn+S-1 = Рn+S-1 = 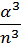 · · 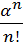 Р0
:
:
Рn+m = Р0
:
:
Рn+m = 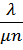 Рn+m+1= Рn+m+1=  · · 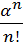 Р0 Р0
|
Сумма вероятностей всех состояний системы = 1, то есть
 , (5.18)
, (5.18)
откуда
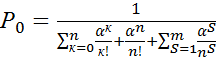 . (5.19)
. (5.19)
Пример: (смотри предыдущий пример) λ = 5; μ = 3; n = 2 и m = 2
Решение:
1.
| Нет очереди |
| Возникает очередь |
| х2 к=2 |
| х0 к=0 |
| х1 к=1 |
| х3 S=1 |
| 2μ |
| хп S=2 |
| λ |
| λ |
| λ |
| λ |
| μ |
| 2μ |
| 2μ |
Рис. 5.4. Граф состояний двухканальной СМО с двумя местами в очереди
2. Определим приведенную плотность α
α=  1,67
1,67
3. Вероятность состояния х0, полного простоя станции
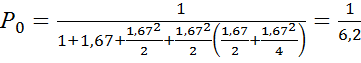 =0,16
=0,16
4. Вероятность состояний системы до возникновения очереди
Р1 = α Р0 = 1,67∙0,16 = 0,27; 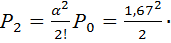 0,16 = 0,225
0,16 = 0,225
5. Вероятность состояний после возникновения очереди
Р3 = 
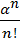 Р0 =
Р0 =  0,16 = 0,186
0,16 = 0,186
Р4 = 
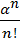 Р0 =
Р0 = 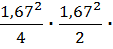 0,16 = 0,159
0,16 = 0,159
Проверка
 0,16 + 0,27 + 0,225 + 0,186 + 0,159 = 1
0,16 + 0,27 + 0,225 + 0,186 + 0,159 = 1
6. Вероятность отказа Ротк = Р4 = 0,159
7. Относительная пропускная способность станции
qотн =1- Ротк = 1- 0,159 = 0,841 (в предыдущем примере 0,656)
То есть 84% автомобилей будут обслужены.
8. Абсолютная пропускная способность станции
за 1 ч → Qабс = λ · qотн = 5 · 0,841 = 4,205 авт./ч
за 10 ч → 42,05 авт. (в предыдущем примере ≈ 32,8 авт.)
9. Номинальная (max) пропускная способность станции
Qmax = μ·t·n = 3·10·2 = 60 авт.
10. Отношение 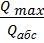 = 1,42 (в предыдущем примере →1,83)
= 1,42 (в предыдущем примере →1,83)
11. Среднее число занятых каналов
М(к) =  +
+  = 1 · 0,27 + 2 · 0,225 + 2(0.186+0
= 1 · 0,27 + 2 · 0,225 + 2(0.186+0
159) = 1,728 канала (в предыдущем примере →1,098)
12. Средняя длина очереди
М (S) =  = 1· 0,186 + 2· 0,159 = 0,504 автомобиля.
= 1· 0,186 + 2· 0,159 = 0,504 автомобиля.
13. Среднее время ожидания в очереди
 =
= 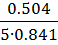 = 0.12 часа.
= 0.12 часа.
14. Среднее время пребывания автомобиля в системе
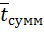 =
= 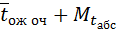 = 0,12 + 0,333 = 0,453 часа.
= 0,12 + 0,333 = 0,453 часа.
Из рассмотренных примеров наглядно видно, что эффективность системы повышается с увеличением числа каналов обслуживания и при наличии очереди. Однако, при этом повышаются и затраты на содержание системы.
|
|
|
|
|
|


