Тема 4. Комбинаторные методы решения логических задач

1. Повторение определений основных понятий темы.

2. Решить задачи.

а) В городе проходит футбольное первенство, в котором участвуют 8 команд. Разыгрываются золотые, серебряные и бронзовые медали (медали получает одна команда). Сколько различных вариантов распределения медалей существует?

б) Сколькими способами можно распределить 5 должностей между 5 лицами, избранными в президиум научного общества?

в) В полуфинале первенства России по шахматам участвуют 10 человек. В финал выходят 3 человека. Определить число различных исходов полуфинала шахматного турнира.

г) Автомобильные номера состоят из трех букв (всего 30 букв) и четырех цифр (используется 10 цифр). Сколько автомобилей можно пронумеровать таким способом, чтобы никакие два автомобили не имели одинаковые номера?

д) Сколько наборов из 7 пирожных можно составить, если в продаже имеется 4 сорта пирожных?

На дом

а) Группа состоит из 25 человек. Необходимо выбрать старосту, заместителя старосты и профорга. Сколькими способами может быть сделан этот выбор, если каждый член группы может занимать лишь один пост?

б) В магазине имеется 10 ящиков для размещения сумок покупателей. В магазин пришло 10 покупателей. Сколькими способами они могут разместить свои сумки?

в) Сколько существует способов распределения 4 билетов на дискотеку между 20 студентами группы, если каждому студент может получить не больше 1 билета? А сколько существует способов распределения, если 2 билета выделяются девушкам, а 2 – юношам (в группе 8 юношей и 12 девушек)?

г) Сколько различных двухзначных чисел можно образовать из цифр 1,2,3,4.

д) Сколько различных букетов из 9 цветов можно составить, если в продаже имеется 5 видов цветов?

3. Решить задачи, используя бином Ньютона.

а) Найдите наибольший коэффициент разложения (a+b)ⁿ, если сумма всех коэффициентов равна 4096.

б) Найдите член разложения , не содержащий х.

На дом

а) Найдите член разложения 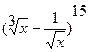, не содержащий х.

б) Коэффициент х во втором члене разложения равен 31. Найдите степень n.

4. Возвести в шестую степень двучлен, используя треугольник Паскаля для нахождения биномиальных коэффициентов:

(1+ x) на дом (x ²– y).

Лучше уменьшить число задач на бином, введя логическую комбинаторную задачу

Тема 5. Формализация бинарных отношений и двуместных

Предикатов в виде графов

Занятие 1

1. Повторение определений основных понятий темы.

2. Для графа, представленного следующей матрицей инциденций, определить матрицу смежности и нарисовать диаграмму графа.

а) на дом б)

3. Для орграфа, представленного следующей матрицей смежности, определить матрицу инциденций и нарисовать диаграмму орграфа:

а) б)

 

4. Нарисовать диаграмму орграфа G=<V, X> и определить, будет ли он связным, сильно связным или несвязным.

V= { v₁, v₂, v_3,, v₄, v₅ },

X= { <v₁, v₂>,<v₂, v₁>,<v₂, v₂>,<v₂, v₃>,<v₂, v₄>,<v₄, v₃>,<v₄, v₂>,<v₄,v₁> }

На дом

V= { v₁, v₂, v_3,, v₄, v₅ },

X= { <v₁, v₂>,<v₂, v₁>,<v₂, v₃>,<v₃, v₁>,<v₃, v₃>,<v₄, v₁>,<v₅, v₅> }.

3. На приведенных ниже рисунках изображены графы G₁ и G₂. Найти G₁ U G₂ и G₁ × G₂.

x₁ x₂ x₁ x₁ x₂ x₁

G₁ G₂G₁ G₂

x₄ x₃ x₃ x₂ x₄ x₃ x₃ x₂

А) б)

на дом

x₁ x₂ x₁

G₁ G₂

x₄ x₃ x₃ x₂

Занятие 2

1. Повторение определений основных понятий темы.

2. По заданной матрице расстояний графа G найти величину минимального пути и сам путь от вершины х₁ до вершины х₆, а затем величину максимального пути и сам путь между теми же вершинами.

на дом

3. По заданной матрице пропускной способностей дуг графа G найти максимальный поток от s=x₁ вершины до вершины t=x₇ и указать минимальный разрез, отделяющий s от t.

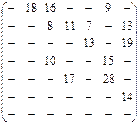на дом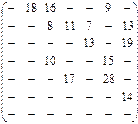

Занятие 3

1. Повторение определений основных понятий темы.

2. В результате опроса сотрудников отдела была получена социометрическая матрица, представленная ниже. Найти для каждого сотрудника индексы: социометрического статуса, эмоциональной экспансивности(Индекс экспансивности (деловой и эмоциональной) является объективной мерой отношения личности к коллективу и характеризует его потребности (во взаимодействии или общении)), объема взаимодействий, а также индексы эмоциональной экспансивности группы и психологической взаимности. Построить концентрическую социограмму.

№	Фамилия
	Анисимов	-	+			+			-
	Бобров	+	-		+	+
	Денисов	-	+	-	+	+
	Ефремов		+		-	+				-
	Жилкин	+			+	-	+	-
	Иванов	+				+	-
	Левитин		-		-			-		+
	Москалев	-		+	+				-
	Якин		+					+		-

 

На дом

№	Фамилия
	Анисимов	-	+	-		+	+		-
	Бобров	+	-	+	+			-		+
	Денисов			-					+
	Ефремов		+	+	-	+		-	+
	Жилкин	+	+	+	+	-	+
	Иванов					+	-
	Левитин					-		-		+
	Москалев	-							-
	Якин				-			+		-

 

 

⇐ Предыдущая123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: