 |
Программа Подбора параметра
|
|
|
|
Цель работы – освоение навыков работы с программой табличного процессора Подбор параметра для решения нелинейных уравнений.
Основные сведения
Программа Подбор параметра в составе табличного процессора Excel используется для решения нелинейных уравнений. Она изменяет значение параметра (переменной) в выражении так, чтобы добиться равенства этого выражения заданному числу. Для подбора используется метод итераций (последовательных приближений).
Для решения каждого уравнения необходимо выполнить следующую последовательность действий.
1. При необходимости преобразовать исходное уравнение так, чтобы в его правой части оставалось только постоянная величина.
2. Ввести в одной из ячеек рабочего листа требуемую формулу (левую часть уравнения). Ячейка с формулой называется целевой.
При написании формулы необходимо ссылаться на одну из ячеек, в которую будет занесено значение параметра x. Ячейка с параметром x (она используется в выражении для целевой ячейки) называются влияющей или изменяемой.
В другие ячейки записать необходимые константы (они являются исходными данными).
При вводе формул необходимо соблюдать правила их написания (формулы начинаются со знака равенства, содержат только числа и ссылки на адреса ячеек, встроенные функции содержат скобки и т.д.)
3. Установить в ячейке с параметром x некоторое допустимое число, при котором результатом вычисления по формуле в целевой ячейке будет число.
4. Задать настройки функции подбора параметра (при необходимости). Для этого зайти на вкладку Вычисления в окне Параметры (команда главного меню Сервис→Параметры…). По умолчанию относительное приращение параметра (относительная погрешность) на соседних итерациях равно 0,001, а предельное число итераций равно 100.
|
|
|
5. Выделить целевую ячейку. Вызвать функцию подбора параметра, выбрав в главном меню Сервис→Подбор параметра…
В появившемся окне в поле Значение указать число в правой части уравнения (а не ссылку на ячейку с этим числом), которому должно равняться выражение в целевой ячейке.
В поле Изменяя значение ячейки задать ссылку на ячейку с параметром (или выбрать эту ячейку в рабочем листе). Нажать ОК.
6. В результате расчетов в ячейке с параметром появится искомое число – корень уравнения.
Функция подбора параметра выдаст окно Результат подбора параметра. Сохранить результат, нажав ОК. Если результат сохранять не нужно, то нажать Отмена, при этом будут сохранены исходные данные на рабочем листе. С помощью кнопки Пауза можно прервать итерационный процесс подбора.
Задания
1. Определить одно из значений параметра x, при котором выражение 
равно 5,7850 с точностью до 4 знаков после десятичной запятой. Здесь постоянная a = 0,6923.
Воспользоваться функцией подбора параметра табличного процессора. Установить приращение параметра на соседних итерациях 0,0001 или предельное число итераций, равное 200.
Убедится в совпадении правой и левой частей уравнения при найденном значении корня.
2. Рассчитать таблицу корней указанного выше уравнении при 8 значениях постоянной a (от 0,25 с шагом 0,1). Таблица расчетов имеет следующий вид.
| Номер уравнения i | Значение a | Выражение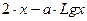 
(целевая ячейка)
| Корень уравнения (изменяемая ячейка) | Абсолютная погрешность
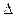
| Относительная погрешность
|
Выяснить, какие формулы таблицы могут распространяться (копироваться).
Абсолютная погрешность вычисления 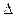определяется как абсолютная разность между значением числа в правой части уравнения и полученным в результате вычисления значением в целевой ячейке. Относительная погрешность оценивается путем деления абсолютной погрешности на модуль значения в целевой ячейке.
|
|
|
3. Найти любое допустимое решение нелинейного уравнения:
,
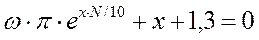где постоянная ω = 0,4275. Определить погрешности.
Решение найти при числе итераций, равном 200. Воспользоваться программой подбора параметра табличного процессора.
Убедиться в совпадении правой и левой частей уравнения при найденном значении корня с точностью до погрешности поиска.
4. Найти любое допустимое решение нелинейного уравнения:
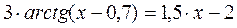
Воспользоваться функцией подбора параметра табличного процессора. В качестве исходного значения параметра для этого уравнения ввести x = -1.
Определить абсолютную и относительную погрешность решения при наибольшем числе шагов, равным 100.
Убедиться, что при некоторых исходных данных решение может не быть найдено (итерационный процесс расходится).
5. Найти все корни нелинейного уравнения 
. Предварительно определить интервалы неопределенности для каждого корня, рассчитав таблицу изменения левой части уравнения y(x)= 0.
Фон ячеек с найденными корнями уравнений раскрасить в светло-зеленый цвет (фон остальных ячеек не изменять).
Домашняя работа
1. Решить с помощью функции подбора параметра нелинейное уравнение:
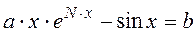
с точностью до четырех десятичных знаков после десятичной запятой. Здесь постоянные величины: N - номер варианта студента, a = 4,12* N /15; b = 0,94. Убедится в правильности найденного корня.
2. С помощью функции поиска параметра найти любое решение нелинейного уравнения:
,
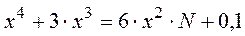предусмотрев 150 итераций. Убедиться в правильности значения найденного корня.
Отчет по проделанной работе должен включать:
-название темы, Ф.И.О. студента, наименование факультета и номер группы, индивидуальный номер варианта N,
-формулировку исходных задач,
-процесс решения и результаты решения каждой задачи с необходимыми пояснениями.
Вопросы
1. Для каких целей служит программа подбора параметра в составе табличного процессора?
2. Какая ячейка называется целевой?
3. Какая ячейка называется влияющей или изменяемой?
|
|
|
4. Найдите ошибки в написании выражения для целевой ячейки: A12*И8/ПИ-EXP^2(q3)=5.
5. Какой математический метод используется для подбора значения корня уравнения (неизвестного параметра)?
6. Сколько корней уравнений может находить программа подбора параметра?
7. Всегда ли процесс подбора завершается успешно? По какой причине?
8. Как вызвать программу подбора параметра?
9. Какие настройки есть у программы подбора параметра? Как их установить?
10. Что нужно заполнить в диалоговом окне перед запуском программы?
11. Как убедится в том, что программа нашла приближенный корень?
12. Что ограничивает применение программы подбора параметра для решения инженерных задач?
ПРОГРАММА ПОИСКА РЕШЕНИЯ
Цель работы – освоение встроенной программы поиска решения нелинейных уравнений, линейных и нелинейных систем уравнений, а также задач оптимизации.
Основные сведения
Программа Поиск решения в составе табличного процессора Excel предназначена для решения уравнений, систем уравнений и задач оптимизации с различными видами граничных условий.
Прежде чем приступить к выполнению заданий, следует убедиться в наличии программы Поиск решения… в меню Сервис. При ее отсутствии выполнить команды Сервис→Надстройки…, и в появившемся окне Надстройки установить метку напротив соответствующей позиции.
Порядок решения уравнений, систем уравнений и оптимизационных задач включает несколько этапов:
1. Формализованная постановка задачи.
2. Создание модели вычислений на рабочем листе табличного процессора.
3. Дополнительная настройка программы.
4. Поиск решения с помощью программы в составе табличного процессора.
5. Анализ результатов.
Этап постановки задачи.
На этапе постановки определяют, какую математическую задачу необходимо решить (уравнение, систему уравнений, задачу оптимизации), какие переменные используются, какая зависимость существует для уравнений, неравенств и критериальной функции от выявленных переменных, какие есть ограничения (граничные условия) и как они зависят от входящих переменных. Результатом этого этапа является формализованная запись задачи на бумаге. При необходимости осуществляется предварительное преобразование задачи к требуемому виду.
|
|
|
|
|
|
