 |
Этап создания модели вычислений.
|
|
|
|
На этапе создания модели вычислений производят запись содержания задачи на листе табличного процессора. При этом необходимо:
1. Выбрать ячейки листа, где будут находиться найденные программой значения переменных (неизвестных). Эти ячейки называются изменяемыми, так как программа последовательно изменяет их значения в итерационном процессе до получения допустимого решения.
2. Записать формулу левой части одного из уравнений системы или целевой функции в отдельной ячейке. Эта ячейка называется целевой. При записи формулы необходимо использовать адреса выбранных ячеек с переменными.
3. Выражение в левой и правой частях для других уравнений в системе или каждого ограничения записать в виде формулы в отдельной ячейке листа. При записи формул использовать адреса выбранных ячеек с переменными.
Каждой ячейке, используемой в модели вычислений, желательно присвоить имя, или дать пояснения в соседних ячейках.
Этап настройки.
Перед запуском программы п ри необходимости можно указать особые, отличные от установленных по умолчанию, условия и варианты поиска решения. Для этого в Excel следует использовать диалоговое окно Параметры поиска решения, в которое можно зайти из окна Поиск решения, нажав кнопку Параметры.
В свою очередь это окно включает следующие диалоговые окна и переключатели.
Окно Максимальное время служит для ограничения времени в секундах на поиск решения. Наибольшее допустимое время равно 32767 секунд (более 9 часов). По умолчанию устанавливается 100 секунд, что обычно бывает достаточно.
Окно Число итераций также ограничивает время вычисления за счет ограничения числа шагов для достижения решения (числа итераций).
|
|
|
Окно Относительная погрешность служит для указания того, насколько найденное решение может отклоняться от установленного значения в целевой ячейке. Она задается в виде десятичной дроби в интервале между нулем и единицей.
Окно Допустимое отклонение служит для задания максимального допуска на отклонение для значения изменяемой ячейки, если множество значений ограничено целыми числами. Чем больше допуск, тем быстрее будет найдено решение.
Окно Сходимость также определяет условие прекращения поиска. Когда относительное изменение значения целевой функции за последние пять итераций становится меньше порога (числа, указанного в поле Сходимость), то поиск прекращается. Сходимость применяется только к нелинейным задачам, условием служит десятичная дробь от 0 до 1. Лучшая сходимость (с меньшим дробным числом) требует больше времени на поиск оптимального решения.
Метка Линейная модель предназначена для ускорения поиска, если решается задача линейной оптимизации.
Опция Показывать результаты итераций используется для приостановки поиска и просмотра результатов после каждой итерации.
Опция Автоматическое масштабирование необходима, если значения в изменяемых ячейках по величине сильно отличаются от выходных значений в целевой ячейке и в ограничениях.
Опция Значения не отрицательны используется, когда для влияющих ячеек не была установлена нулевая нижняя граница в поле Ограничения диалогового окна Добавить ограничение.
Переключатель Оценка служит для указания метода получения оценок значений переменных в каждом одномерном поиске (Линейная или Квадратичная). Квадратичная экстраполяция, используемая для получения оценок, более точна и обычно применяется в нелинейных задачах.
Переключатель Производные служит для указания метода численного дифференцирования — Прямые (используются в большинстве задач) или Центральные (используются, когда выдается сообщение о том, что получить более точное решение не удается).
|
|
|
Переключатель Метод служит для выбора алгоритма оптимизации - метод Ньютона (для задач небольшой размерности и для хорошо сходящихся задач) или сопряженных градиентов (для задач большой размерности и когда итерации дают слишком малое отличие в последовательных приближениях).
Опция Загрузить модель позволяет задать ссылку на область ячеек, содержащих загружаемую модель.
Опция Сохранить модель позволяет задать ссылку на область ячеек, предназначенную для хранения модели оптимизации, если необходимо хранить на листе более одной модели оптимизации. Первая модель сохраняется автоматически.
Этап вычислений.
На этапевычисления следует обратиться к программе, выбрав Поиск решения… в меню Сервис. В открывшемся окне Поиск решения произвести основные установки.
1. В окне Установить целевую ячейку указать адрес ячейки с введенной формулой для целевой функции или левой частью уравнения. Он появится автоматически, если перед вызовом программы нужная ячейка будет активизирована.
2. В меню Равно указать вариант оптимизации (максимизация, минимизация). Если ставится задача поиска решения, при котором целевая функция должна быть равна некоторому числу, то необходимо ввести это число в поле. Требование равенства целевой функции определенному числу означает решение уравнений и систем уравнений.
3. В окне Изменяя ячейки указать адреса выбранных ранее ячеек (или выделить соответствующие ячейки) для переменных (неизвестных) в целевой функции или в уравнении. При нажатой клавише Ctrl можно выделить несмежные ячейки. В этих ячейка будут изменяться значения переменных в процессе поиска решения до тех пор, пока не будут выполнены наложенные ограничения и условие оптимизации. С помощью программы можно решать задачи, включающие до 200 переменных.
Для каждой изменяемой ячейки можно указать два ограничения.
Адреса в поле Изменяя ячейки могут появиться автоматически, если установить метку Предположить,и предварительно указать начальные значения переменных. Тогда программа самостоятельно находит все ячейки, влияющие на формулу, ссылка на которую дана в поле Установить целевую ячейку.
|
|
|
4. В поле Ограничения отобразить все граничные условия поставленной задачи. Для каждой переменной или для каждого выражения с этими переменными можно задать диапазон (верхнюю и/или нижнюю границы) допустимых значений.
Указать адреса ячеек с записанными в них формулами для ограничений. Для этого использовать кнопки Добавить, Изменить, Удалить для выбранных ограничений.
Для целевой ячейки также можно установить ограничения.
Для удобства можно выбрать ячейки по их именам из предлагаемого списка после нажатия клавиши F3. Предварительно нужно задать ячейкам имена.
Для присвоения имени ячейке или диапазону ячеек нужно их выделить, поместить курсор в поле имени и заменить представленный адрес нужным именем. Затем нажать клавишу Enter. Присвоенное имя будет отображено в поле имени.
5. Решить уравнение, систему уравнений или задачу оптимизацию, нажав кнопку Выполнить в окне поиска решения. Результаты появятся на листе с вычислительной моделью и в окне диалога Результаты поиска решения.
Этап анализ результатов.
Программа после отдельного запуска может найти только одно из возможных решений. Это являться существенным ограничением программы, требующим дополнительного анализа задачи и результатов, а в некоторых случаях и уточнения условий задачи.
В результате поиска в ячейках листа появятся значения, определяемые найденными переменными. Программа может найти такое решение, которое противоречит физическому смыслу задачи и потому не удовлетворяет специалиста. Она может вообще не найти никакого допустимого решения, или найти решение с недостаточной точностью. Каждый случай требует дополнительного анализа.
Если решение находится в неприемлемой области, противоречит физическому смыслу задачи, то следует провести дополнительное исследование задачи и ввести дополнительные граничные условия. После этого нужно повторить расчет. С этой проблемой иногда можно справиться, сразу задавая начальные значения переменных из ожидаемой области решений.
|
|
|
Если хотя бы одно из требований в результате поиска не удовлетворяется, то программа не смогла найти допустимое решение. В этом случае необходимо выбрать другие исходные данные для переменных, или увеличить число итераций, или изменить метод поиска. Если допустимое решение не достигнуто, то следует проанализировать инженерную задачу и по возможности ослабить ограничения.
Недостатком программы поиска является высокая чувствительность к начальным значениям неизвестных. Если начальные значения неизвестных выбраны неудачно, то решение может не быть найдено, хотя оно существует.
При выполнении программы Поиск решения следует анализировать выдаваемые программой сообщения. Если решение получено, то сведения о результатах появляются в окне Результаты поиска. Оно включает следующие опции.
Сохранить найденное решение. Служит для сохранения найденного решения во влияющих ячейках модели.
Восстановить исходные значения. Используется для восстановления исходных значений влияющих ячеек модели.
Отчеты. Служит для указания типа отчета, для которого создается отдельный лист рабочей книги.
Отчет Результаты включает целевую ячейку и список влияющих ячеек модели, их исходных и конечных значений, а также формулы ограничений и дополнительные сведений о наложенных ограничениях.
Отчет Устойчивость содержит сведения о чувствительности решения к малым изменениям в формуле целевой ячейки или в формулах ограничений. Он не создается для моделей с целочисленными переменными. В случае нелинейных моделей отчет содержит данные для градиентов и множителей Лагранжа.
Отчет Ограничения (отчет по пределам) включает целевую ячейку и список влияющих ячеек модели, их значений, а также нижние и верхние границы для изменяемых ячеек. Такой отчет не создается для моделей, значения в которых ограничены множеством целых чисел. Нижним пределом является наименьшее значение, которое может содержать влияющая ячейка, при этом значения остальных влияющих ячеек фиксированы и удовлетворяют наложенным ограничениям. Соответственно, верхним пределом называется наибольшее значение.
Опция Сохранить сценарий служит для сохранения сценария решения задачи для его использования с помощью диспетчера сценариев Excel.
Задания
1. С помощью программы Поиск решения решить с 6 десятичными разрядами нелинейное уравнение
при удовлетворении граничного условия:
Вначале преобразовать исходное уравнение так, чтобы в его правой части содержалось только число: 
Создать рабочий лист, назвать его “Поиск”. На этом листе будет записана формализованная вычислительная модель для задания.
|
|
|
В ячейке B1 поместить начальное значение переменной x (любое значение из допустимой области, например, 0). Эта ячейка называется изменяемой. В нее можно не записывать никаких начальных значений, и тогда программа устанавливает свои значения.
В ячейке B2 нужно записать выражение для левой части уравнения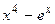 
. Эта ячейка является целевой. Выражение – это формула, поэтому оно начинается со знака равно (=). В выражении необходимо использовать адреса с переменной и исходными данными. В этом задании при записи выражения необходимо использовать адрес ячейки B1 для переменной x и встроенную функцию экспоненты.
Комментарии (поясняющий текст) к используемым ячейкам следует поместить слева в ячейках A1 и A2 (например: X, Уравнение, Переменная, и т.д.). На процесс поиска решения комментарии не влияют, они служат для лучшего понимания структуры задачи и в целом для удобства.
Массив ячеек A1:B2 представляет собой вычислительную модель.
Активизировать целевую ячейку B2 с левой частью уравнения. Затем вызвать окно поиска решения Сервис→Поиск решения…
В появившемся окне Поиск решения:
- в пункте Установить целевую ячейку: выбрать адрес B2. Она появится автоматически, если эта ячейка была активизирована до вызова программы;
- в пункте Равной установить метку, а в окне значению: установить число 1,7 из правой части уравнения;
- в пункте Изменяемые ячейки: выбрать ячейку с переменной B1. Она будет установлена автоматически, только если в нее было занесено начальное значение, и если выбрать пункт Предположить;
- в меню Ограничения: установить ограничение для данной задачи B1>=0. Для этого воспользоваться кнопками Добавить, Изменить, Удалить.
Нажать кнопку Выполнить. В ячейках B1:B2 появятся найденные в результате поиска значения.
Проверить удовлетворение условий задачи. Должно выполняться: B1>=0, B2=1,7.
Если одно из этих требований не выполняется, то программа не смогла найти допустимое решение. В этом случае следует повторить поиск, выбрав другие начальные значения переменных из допустимой области, или увеличить число итераций в окне Параметры поиска решения, или выбрав другой метод поиска.
Добиться получения допустимого решения: x =1,608615.
2. С помощью программы Поиск решения решить с 5 знаками после запятой нелинейное уравнение
при удовлетворении граничного условия:
Вычислительную модель записать на том же листе. После получения решения проверить удовлетворение условий задачи.
3. С помощью программы Поиск решения решить с 3 знаками после запятой систему нелинейных уравнений с двумя неизвестными:
при удовлетворении граничного условия:
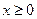
Вначале необходимо преобразовать систему так, чтобы в одном из уравнений его правая часть содержала постоянное число. Эта правая часть в дальнейшем будет записана в целевую ячейку. Преобразование можно сделать различным образом. Один из вариантов такого преобразования приводит к системе уравнений:
Если будет найдено решение x =1,3, то оно должно будет отброшено как недопустимое, так как в результате преобразования расширена область допустимых значений.
На отдельном листе с именем “Системы” в ячейке B1 будет находиться изменяемая переменная x, а в ячейке B2 – изменяемая переменная y.
Целевой функцией является выражение в левой части преобразованного уравнения 
. Его следует занести в ячейку B3, являющуюся целевой.
Выражение в левой части второго уравнения 
занести в ячейку B4, а выражение в правой части 
в ячейку B5. Выражение для левой части неравенства уже содержится в ячейке B1.
Все выражения нужно записывать по правилам написания формул с применением адресов ячеек, в которых находятся значения переменных.
Вычислительную модель дополнить комментариями к выбранным ячейкам.
Активизировать целевую ячейку B3.
Вызвать из меню Сервис→Поиск решения… диалоговое окно Поиск решения. В нем:
- в пункте Установить целевую ячейку: выбрать адрес B3. Он появится автоматически, если целевая ячейка была активизирована до вызова программы;
- в пункте Равной установить метку перед опцией значению:, а в соседнем окне установить число 2 (из правой части преобразованного уравнения);
- в пункте Изменяемые ячейки: выбрать ячейки с переменными B1 и B2. При необходимости последовательного выбора нужно удерживать клавишу Ctrl;
- в меню Ограничения: установить ограничения B4=B5 и B1>=0. Для этого воспользоваться кнопками Добавить, Изменить, Удалить.
Нажать кнопку Выполнить. В ячейках B1:B5 появятся найденные в результате поиска значения.
Проверить удовлетворение условий задачи. Должно выполняться: B1>=0, B3=2; B4=B5.
Добиться получения допустимого решения x =2,262; y = 2,078.
4. С помощью программы Поиск решения решить систему нелинейных уравнений:
при удовлетворении граничного условия:
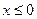
Вычислительную модель записать на лист “Системы”. После получения решения проверить удовлетворение условий задачи. Добиться получения допустимого решения: x =-1,200; y =-0,800.
5. С помощью программы Поиск решения решить оптимизационную задачу:
при условиях:
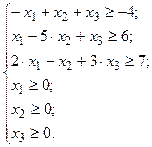
Решить оптимизационную задачу – это значит найти значения переменных 
, при которых целевая (критериальная) функция 
принимает наименьшее значение, и при этом удовлетворяются заданные граничные условия.
В этой оптимизационной задаче целевая функция и все ограничения представляют собой линейные функции от переменных , поэтому она называется задачей линейного программирования (линейной оптимизации).
На отдельном листе с именем “Оптимизация” выделить ячейки под каждую переменную (неизвестную величину). Записать в выбранную целевую ячейку выражение для целевой функции. Выражения для левых частей неравенств также записать в отдельные ячейки.
Дополнить модель комментариями к каждой используемой ячейке.
В окне Поиск решения:
- выбрать адрес целевой ячейки с записью целевой функции,
- установить метку в пункте Равной перед опцией минимальному значению,
- указать все ячейки с переменными в окне Изменяя ячейки:, используя клавишу Ctrl (или использовать кнопку Предположить, если были заданы начальные значения переменных),
- отразить каждое ограничение в окне Ограничения:, при этом делается ссылка на соответствующие ячейки с формулами и с неизвестными. Исходные неравенства удобно предварительно преобразовать, оставив в левой части указание на одну из переменных.
Для ускорения поиска установить метку Линейная модель в окне Параметры поиска решения.
Добиться решения 
.
6. Решить задачу нелинейной оптимизации:
при ограничениях:
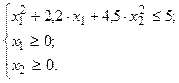
Критериальная функция и одно из ограничений имеют степень второго порядка. Поэтому такая задача называется задачей квадратичной оптимизации.
Вычислительную модель записать на лист “Оптимизация”. После получения решения проверить удовлетворение условий задачи.
Проверить правильность решения 
.
7. Решить задачу оптимизации:
при ограничениях:
Особенность этой задачи состоит в том, что в ней заданы требования целочисленности переменных. Такая задача называется задачей целочисленного программирования (оптимизации).
В окне Ограничения: необходимо выбрать для переменных условие целое. Ячейки с целыми переменными должны быть смежными.
Если условие целочисленности в этой задаче не налагается, то оптимальным решением является 
. Простое округление этих значений до целых не приведет к правильному решению, то есть решение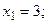 
не является оптимальным. Поэтому для целочисленных задач применяют специальные методы.
Вычислительную модель записать на лист “Оптимизация”. После получения решения проверить удовлетворение условий задачи.
Создать отчеты Результаты, Устойчивость, Ограничения. Объяснить их содержание.
Таким же образом в окне Ограничения: при необходимости устанавливаются требования к булевым (двоичным) переменным, которые могут принимать только два значения: 0 или 1. Такие задачи называются задачами булевого программирования (оптимизации).
Домашняя работа
Использовать встроенную в табличный процессор программу Поиск решения с исходными установками для выполнения следующих заданий.
1. Решить нелинейное уравнение 
.
2. Решить нелинейное уравнение 
, если требуемый корень отделен на отрезке (-π/2; 3).
3. Решить систему нелинейных уравнений
4. Решить задачу линейного программирования. Найти минимальное значение функции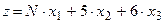 
при ограничениях: 
5. Решить задачу нелинейной оптимизации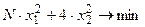 
при условиях - неравенствах: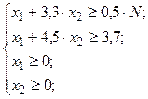 
6. Решить задачу целочисленной оптимизации 
при ограничениях: 
Отчет по проделанной работе должен включать:
-название темы, Ф.И.О. студента, наименование факультета, курс и номер группы, индивидуальный номер варианта N,
-формулировку каждой задачи с индивидуальными исходными данными;
-характеристику каждой задачи (характеристика целевой функции, уравнений, неравенств, неизвестных),
-вычислительную модель с комментариями,
-проверку выполнения ограничений в задачах,
-найденные с помощью программы Поиск решения значения переменных (неизвестных), значение целевой функции в оптимизационных задачах.
Вопросы
1. Для каких целей используется программа Поиск решения в составе табличного процессора? Как ее вызвать?
2. Указать основные этапы поиска решений инженерных задач.
3. В чем состоит этап формализованной постановки задачи?
4. В чем состоит этап построения вычислительной модели применительно к использованию табличного процессора?
5. Что проверяется на этапе анализа решения?
6. Какая функция в оптимизационных задачах называется целевой или критериальной?
7. Какой вид могут иметь ограничения оптимизационной задачи?
8. Почему для задач целочисленного программирования нельзя использовать решения для непрерывных задач оптимизации?
9. Какие переменные называются булевыми? Какие задачи называются задачами булевого программирования (оптимизации)?
10. Какая ячейка на рабочем листе называется целевой применительно к программе Поиск решения? Для чего она служит?
11. Какие математические методы поиска реализуются в программе Поиск решения?
12. Как в программе задать требуемую точность поиска решения?
13. Как в программе задать требование целочисленности решения?
14. Какие сообщения может выдавать программа после выполнения вычислений, и в каких случаях?
15. Какие действия необходимо предпринять, если найденное допустимое по условиям задачи решение является неприемлемым по его физическому смыслу?
16. Какие действия необходимо предпринять, если допустимое решение в результате поиска не найдено?
17. Какие отчеты могут быть созданы с помощью программы? Что в них содержится?
18. Какие особенности программы Поиск решения ограничивают ее применение?
19. Указать порядок работы с программой Поиск решения при решении уравнений и систем уравнений.
20. Указать порядок работы с программой Поиск решения при решении задач оптимизации.
Рекомендуемая литература: [4], [13], [17], [19].
|
|
|
