 |
Представление структурных схем с помощью графов
|
|
|
|
Все структурные схемы имеют нечто общее, и это побудило рассматривать их как особый объект математических исследований. Для этого пришлось абстрагироваться от содержательной стороны структурных схем. В результате получилась схема, в которой обозначается только наличие элементов и связей между ними, а также (в случае необходимости) разница между элементами и между связями. Такая схема называется графом (рис. 16).

Рис. 16. Изображение структурной схемы с помощью графа
Следовательно, граф состоит из: обозначений элементов произвольной природы, называемых вершинами; обозначений связей между ними, называемых ребрами. Часто бывает необходимо отразить несимметричность некоторых связей; в таких случаях линию, изображающую ребро, снабжают стрелкой. Если направления не обозначаются, то граф называется неориентированным, при наличии стрелок – ориентированным (полностью или частично). Данная пара вершин может быть соединена любым количеством ребер; вершина может быть соединена сама с собой (тогда ребро называется петлей). Если в графе требуется отразить другие различия между элементами или связями, то либо приписывают разным ребрам различные веса (взвешенные графы), либо раскрашивают вершины или ребра (раскрашенные графы). Для графов построена теория, имеющая многочисленные приложения. Разнообразные задачи этой теории связаны с различными преобразованиями графов, а также с возможностью рассмотрения различных отношений на графах: весов, рангов, цветов, вероятностных характеристик (стохастические графы) и т.п. В связи с тем, что множества вершин и ребер формально можно поменять местами, получается два представления системы в виде:
|
|
|
· вершинного графа;
· реберного графа.
В одних задачах удобнее использовать вершинный, а в других – реберный граф. Графы могут изображать любые структуры, если не накладывать ограничений на пересекаемость ребер. Некоторые типы структур имеют особенности, важные для практики, они выделены из других и получили специальные названия. Так, в организационных системах часто встречаются линейные, древовидные (иерархические) и матричные структуры; в технических системах чаще встречаются сетевые структуры; особое место в теории систем занимают структуры с обратными связями.
Динамические модели систем
До сих пор основное внимание было уделено понятию системы, ее составу и устройству. Были построены модели, которые являются как бы «фотографиями» системы, отображают ее в некоторый момент времени t. В этом смысле рассмотрены варианты моделей «черного ящика», состава, структуры и структурной схемы системы могут быть названы статическими моделями, что подчеркивает их неподвижный, как бы застывший характер.
Понятие динамики системы
Следующий шаг в исследовании систем состоит в том, чтобы понять и описать, как система «работает», что происходит с ней самой и с окружающей средой в ходе реализации поставленной цели.
Очевидно, и подход к описанию, и степень подробности описания происходящих процессов могут быть различными. Однако общим является то, что разрабатываемые модели должны отражать поведение систем, описывать происходящие с течением времени изменения, последовательность каких-то этапов, операций, действий, причинно- следственные связи. Системы, в которых происходят какие бы то ни было изменения со временем, будем называть динамическими, а модели, отображающие эти изменения, – динамическими моделями систем. Термин «динамический» будем использовать как обозначение любых изменений во времени. Для разных объектов и систем разработано большое количество динамических моделей, описывающих процессы с различной степенью детальности: от самого общего понятия динамики, движения вообще, до формальных математических моделей конкретных процессов типа уравнений движения в механике или волновых уравнений в теории поля. Уже на этапе «черного ящика» различают 2 этапа динамики системы: ее функционирование и развитие.
|
|
|
Под функционированием подразумевают процессы, которые происходят в системе (и окружающей ее среде), стабильно реализующей фиксированную цель (например, часы, городской транспорт, кинотеатр, канцелярия, радиоприемник, станок, школа и т.д.) Развитием называют то, что происходит с системой при изменении ее целей. Характерной чертой развития является тот фактор, что существующая структура перестает соответствовать новой цели, и для обеспечения новой функции приходится изменять структуру, а иногда и состав системы, перестраивать всю систему. Не следует считать, что система всегда находится либо в фазе развития, либо в состоянии функционирования. Например, при реконструкции одного цеха остальные функционируют, завод в целом развивается. Даже при коренной перестройке системы какие-то элементы и даже подсистемы старой структуры могут продолжать функционировать в новой по - прежнему. Возможны и такие системы, для функционирования которых какие-то ее подсистемы должны быть постоянно в развитии. Следующий шаг в построении динамических моделей состоит в том, чтобы конкретнее отобразить происходящие изменения. Это означает, что следует различать части, этапы происходящего процесса, рассматривать их взаимосвязи. Другими словами, типы динамических моделей такие же, как и статических, только элементы этих моделей имеют временной характер.
Типы динамических моделей
При математическом моделировании некоторого процесса его конкретная реализация описывается в виде соответствия между элементами множества Х возможных «значений» х и элементов упорядоченного множества Т «моментов времени» t, т.е. в виде отображения:

С помощью этих понятий можно строить математические модели систем (рис. 17). Рассматривая выход y(t) системы (это может быть вектор) как ее реакцию на управляемые u(t) и неуправляемые v(t) входы
|
|
|

можно модель «черного ящика» выразить как совокупность двух процессов:

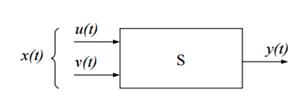
Рис. 17. Модель системы
Если даже считать y(t) результатом некоторого преобразования Ф процесса х(t),т.е. y(t) = Φ [x(t)], то модель «черного ящика» предполагает, что это преобразование неизвестно. В том случае, если имеем дело с «белым ящиком», соответствие между входом и выходом можно описать тем или иным способом. Какой именно способ – зависит от того, что именно нам известно, и в какой форме можно использовать эти знания.
Модель с управлением
Система формально задается как некая упорядоченная последовательность вида:
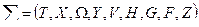 , где
, где
 - ось времени
- ось времени
 - множество входной информации
- множество входной информации
 ,
, 
 - оператор ввода, множество
- оператор ввода, множество  - входных воздействий
- входных воздействий
 - множество результатов
- множество результатов
 - множество выходных воздействий
- множество выходных воздействий
Процесс преобразования входной информации Х в выходную информацию У на оси Т определяется тремя функциональными факторами:
G – алгоритм, функция выхода;
Н – функция поведения системы при использовании ресурсов системы, внутренних состояний, функция перехода;
F – функция управления, изменяющая как, G так и Н;
Z – множество внутренних состояния или ресурсов системы

Перечисленные параметры системы определяют следующие свойства системы ∑:
1) система и ее поведение определяется более чем одним фактором, т.е. система – это энарная функция;
2) наличие фактора времени T говорит о том, что системы могут быть непрерывные, дискретные, динамические и статические;
3) наличие факторов Х и Ω, У и V говорит о том, что система может быть реализована и связана с внешней средой. У системы должно быть 0 или более входов и 1 или более выходов;
4) фактор G говорит о том, что процесс преобразования Х в У может быть формализован по виду входной и выходной информации даже, если не известна внутренняя структура системы;
5) наличие Н, Z – система имеет свой конкретный способ поведения, который влияет на G, а так же H и Z влияет на получение конкретного результата Y;
|
|
|
6) наличие F – система может быть самоуправляемой, самоуправляющей, саморегулируемой или саморегулирующей;
7) наличие множества Е-элементов и связей определяют тот факт, что системы бывают простые и сложные.
Основные характеристики модели с управлением
Сложность системы определяется как структурная и функциональная сложность.
Функциональная сложность CF – количество шагов (счетных и логических), требуемых для реализации конкретно заданной функции F.
CF= (H*L)К, где L – логическая глубина вычислений (длина самой длинной цепочки вычислений, самого длинного пути работы); H – степень параллелизма вычислений (работ); K – степень сложности реализации системы, если система еще не реализована К=1;
Структурная сложность C∑ – некоторая метрическая величина, определяющая количество элементов и количество связей системы.
C∑= m/n(n-1), где m – число реализованных связей в системе между элементами, n – общее число элементов в системе.
Если система реализована, то структурная сложность рассчитывается по формуле
С*=(1+ξ*C∑)* Се, (11) где Се – сложность реализации элементов в системе ξ – относительная величина сложности реализации связей и элементов в системе, т.е. ξ = сложность реализации элементов/сложность реализации связей
Сложность C – это некая метрическая величина, ставящаяся в соответствие структурно- функциональному составу системы.
Надежность R – напрямую зависит от сложности. Это некая метрическая величина, которая определяет способность системы сохранять заданные свойства поведения при наличии внешних и внутренних воздействий, т.е. а) быть устойчивой в смысле функционирования, б) быть помехозащищенной в смысле сохранении элементов и структуры от механических воздействий.
R=f(TH,Tср,P(ti,ti+1),∆(ti,ti+1)), где
1) TH – время нормальной работы системы (время от начала запуска системы до того момента, когда из-за накопившегося числа явных и неявных отказов система «плохо» работает)
2) Тср– среднее время безотказной работы, (вычисляется по наблюдению за работой системы).
3) P(ti,ti+1) или P(∆t) вероятность безотказной работы в интервале ∆t = (ti,ti+1);
4) ∆(ti,ti+1)- средний поток отказов на интервале (ti,ti+1).
Эффективность Э – метрическая величина, определяющая способность системы хорошо выполнять заданную работу.
Эффективность вычисляется через функционал качества Φ и функцию управления.
Φ (X,Zo,∆t,ω) = y ≈ ∋, где
Φ – функция управления,
Э – эффективность,
X – начальные данные (ввод),
Y – конечные данные (вывод),
Zo – начальное состояние (ресурсы),
∆t – интервал работы (времени),
|
|
|
ω – входные воздействия (операторы ввода).
Качество управления системой вычисляется через функцию управления J: J (X,Zo,Zi,g,ω) = {∆ti}
Функция управления J – это некоторая метрическая величина, определяющая минимально допустимый интервал времени ∆tmin, необходимый для завершения работы системы по получению ожидаемого результата.
На практике часто для определения эффективности системы используют дополнительные характеристики системы:
1. Пропускная способность П (если П→1, то имеет место высокая пропускная способность min∆t);
2. Универсальность U (если U→1, то имеет место высокая универсальность и низкая надежность);
3. Степень иерархичности J (определяется по каждому виду иерархии: управление, информация, время, функция, затраты).
Построение модели
Все рассмотренные типы моделей являются формальными, относящимися к любым системам и, следовательно, не относящимся ни к одной конкретной системе. Чтобы получить модель заданной системы, нужно придать формальной модели конкретное содержание, решить какие аспекты реальной системы включать как элементы модели избранного типа, а какие – нет, считая их несущественными. Этот процесс обычно неформализуем, является интеллектуальным, творческим. В процессе построения содержательных моделей систем главной является задача создания полной модели.
Общие рекомендации по достижению полноты:
– необходимо стремиться учесть все существенные факторы, влияющие на рассматриваемое явление; поскольку такая существенность не всегда очевидна, лучше включить в модель несущественный элемент, чем не включить существенный;
– одним из необходимых признаков полноты модели является наличие в ней противоречивых элементов; следует уделить специальное внимание этому моменту: например, при перечислении выходов надо включать в перечень не только желательные целевые выходы (связи, продукцию и т.п.), но и нежелательные (отход, брак, и т.д.);
– как бы ни были обширны знания о данном явлении, реальность богаче моделей – в ней всегда есть неизвестные факторы; чтобы не упустить из виду возможность чего- то существенного, но пока неизвестного, рекомендуется включать в модель неявные «запасные», неконкретизированные элементы (типа «все остальное», «что-то ещё») и на различных стадиях системного анализа обращаться к этим элементам, ставя вопрос: не пора ли дополнить модель ещё одним явным элементом.
|
|
|


