 |
Математические модели функционирования несимметричных, многомаркерных КЛВС с конечнымибуферами различной емкости и ординарной дисциплиной обслуживания
|
|
|
|
1.1 Математическая модель функционирования многомаркерной, несимметричной КЛВС с N АС, с k маркерами (1< k < N) и буферами различной емкости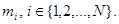 
Рассмотрим несимметричную КЛВС с протоколом маркерного доступа, которая состоит из N абонентских станций, на i-тую АС поступает простейший поток сообщений интенсивности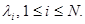 
На каждой АС имеется буфер с емкостью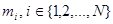 
, который служит для отправки сообщений по кольцу, а также есть приемный буфер, который позволяет принимать любое количество сообщений. АС пронумерованы таким образом, что номер АС увеличивается по направлению движения свободных маркеров, причем после прохождения N-ой АС свободный маркер поступает на первую АС. Для передачи сообщений используются k маркеров, 1<k<N.
Буфер на i-той станции назовем полностью свободным, если на АС нет сообщений для передачи и полностью занятым, если на АС имеется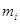 
сообщений, подлежащих передаче.
Если свободный маркер поступает на свободную АС (не содержащую ни одного сообщения), то он немедленно отправляется на очередную АС. Если маркер поступает на АС, где имеется хотя бы одно сообщение, то немедленно начинается передача имеющихся сообщений в соответствии с дисциплиной обслуживания.
Дисциплина обслуживания – ординарная, т.е. при поступлении маркера на АС обслуживается не более одного сообщения, стоящего в очереди в момент прихода маркера.
Будем считать, что во время передачи сообщения все поступающие на эту АС сообщения, подлежащие передаче, теряются. Т.е. в этом случае на АС, с которой передаются сообщения, происходит блокировка буфера, в котором находились сообщения в момент прихода маркера. Время блокировки равно времени передачи сообщения, находившихся на АС-отправителе в момент прихода маркера.
|
|
|
Время перехода свободного маркера между соседними АС будем считать одинаковым для всех станций и равно d. Скорость движения сообщения по кольцу такая же, как и скорость движения свободного маркера. Время, необходимое для передачи и приема сообщения в кольце, обозначим через a.
Интервал времени между последовательными приходами маркеров на станции равен либо D=d+aпри наличии хотя бы одного сообщения для передачи на АС кольца, либо d, если ни на одной АС нет ни одного сообщения для передачи.
После того, как АС-адресат приняла сообщение, квитанция о приеме передается по кольцу на АС-отправитель этого сообщения. При получении квитанции о приеме АС-отправитель освобождается от переданного сообщения, отправляет маркер на очередную АС.
1.2 Математическая модель функционирования многомаркерной, несимметричной КЛВС с буферами 
, с 3 АС и 2-мя маркерами, с ординарной дисциплиной обслуживания
Рассмотрим несимметричную КЛВС с протоколом маркерного доступа, которая состоит из 3 абонентских станций, на i-тую АС поступает простейший поток сообщений интенсивности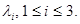 
На первой АС имеется буфер емкостью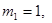 
на второй АС буфер емкостью 
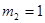, на третьей АС буфер 
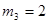, которые служат для отправки сообщений по кольцу, а также есть приемные буфера, которые позволяют принимать любое количество сообщений. АС пронумерованы таким образом, что номер АС увеличивается по направлению движения свободных маркеров, причем после прохождения третьей АС свободный маркер поступает на первую АС. Для передачи сообщений используются 2 маркера.
Буфер на i-той станции назовем полностью свободным, если на АС нет сообщений для передачи и полностью занятым, если на АС имеется 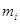сообщений, подлежащих передаче.
Если свободный маркер поступает на свободную АС (не содержащую ни одного сообщения), то он немедленно отправляется на очередную АС. Если маркер поступает на АС, где имеется хотя бы одно сообщение, то немедленно начинается передача имеющихся сообщений в соответствии с дисциплиной обслуживания.
|
|
|
Дисциплина обслуживания – ординарная, т.е. при поступлении маркера на АС обслуживается не более одного сообщения, стоящего в очереди в момент прихода маркера.
Будем считать, что во время передачи сообщения все поступающие на эту АС сообщения, подлежащие передаче, теряются. Т.е. в этом случае на АС, с которой передаются сообщения, происходит блокировка буфера, в котором находились сообщения в момент прихода маркера. Время блокировки равно времени передачи сообщения, находившихся на АС-отправителе в момент прихода маркера.
Время перехода свободного маркера между соседними АС будем считать одинаковым для всех станций и равно d. Скорость движения сообщения по кольцу такая же, как и скорость движения свободного маркера. Время, необходимое для передачи и приема сообщения в кольце, обозначим через a.
Интервал времени между последовательными приходами маркеров на станции равен либо D=d+aпри наличии хотя бы одного сообщения для передачи на АС кольца, либо d, если ни на одной АС нет ни одного сообщения для передачи.
После того, как АС-адресат приняла сообщение, квитанция о приеме передается по кольцу на АС-отправитель этого сообщения. При получении квитанции о приеме АС-отправитель освобождается от переданного сообщения, отправляет маркер на очередную АС.
1.3 Математическая модель функционирования многомаркерной, несимметричной КЛВС с N АС, с k маркерами (k = N) и буферами различной емкости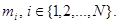 
Рассмотрим несимметричную КЛВС с протоколом маркерного доступа, которая состоит из N абонентских станций, на i-тую АС поступает простейший поток сообщений интенсивности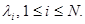
На каждой АС имеется буфер с емкостью 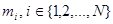, который служит для отправки сообщений по кольцу, а также есть приемный буфер, который позволяет принимать любое количество сообщений. АС пронумерованы таким образом, что номер АС увеличивается по направлению движения свободных маркеров, причем после прохождения N-ой АС свободный маркер поступает на первую АС. Для передачи сообщений используются k маркеров, k=N.
|
|
|
Буфер на i-той станции назовем полностью свободным, если на АС нет сообщений для передачи и полностью занятым, если на АС имеется 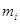сообщений, подлежащих передаче.
Если свободный маркер поступает на свободную АС (не содержащую ни одного сообщения), то он немедленно отправляется на очередную АС. Если маркер поступает на АС, где имеется хотя бы одно сообщение, то немедленно начинается передача имеющихся сообщений в соответствии с дисциплиной обслуживания.
Дисциплина обслуживания – ординарная, т.е. при поступлении маркера на АС обслуживается не более одного сообщения, стоящего в очереди в момент прихода маркера.
Будем считать, что во время передачи сообщения все поступающие на эту АС сообщения, подлежащие передаче, теряются. Т.е. в этом случае на АС, с которой передаются сообщения, происходит блокировка буфера, в котором находились сообщения в момент прихода маркера. Время блокировки равно времени передачи сообщения, находившихся на АС-отправителе в момент прихода маркера.
Время перехода свободного маркера между соседними АС будем считать одинаковым для всех станций и равно d. Скорость движения сообщения по кольцу такая же, как и скорость движения свободного маркера. Время, необходимое для передачи и приема сообщения в кольце, обозначим через a.
Интервал времени между последовательными приходами маркеров на станции равен либо D=d+aпри наличии хотя бы одного сообщения для передачи на АС кольца, либо d, если ни на одной АС нет ни одного сообщения для передачи.
После того, как АС-адресат приняла сообщение, квитанция о приеме передается по кольцу на АС-отправитель этого сообщения. При получении квитанции о приеме АС-отправитель освобождается от переданного сообщения, отправляет маркер на очередную АС.
Данная модель интересна тем, что любая станция может передавать сообщение (если оно имеется). Это объясняется тем, что количество маркеров совпадает с количеством станций. Это модель имеет также особенности и в виде матрицы переходов из одного периодического класса в другой.
2. Определение стационарных вероятностей состояний несимметричных, многомаркерных КЛВС
|
|
|
