 |
Определение стационарных вероятностей состояний многомаркерной, несимметричной КЛВС с буферами различной емкости, с N АС и k маркерами, с ординарной дисциплиной обслуживания
|
|
|
|
Будем рассматривать поведение КЛВС в моменты поступления маркеров на АС. В этом случае изменение состояний КЛВС образуют конечную цепь Маркова.
Под состоянием КЛВС будем понимать состояние всех АС кольца в момент поступления на них маркеров. Каждая АС может находиться всегда в одном из 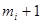
 состоянии.
состоянии.
Все состояния КЛВС делятся на N периодических классов, каждый из которых содержит в рассматриваемом случае 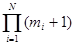 состояние.
состояние.
Особенности протокола приводят к тому, что указанная цепь Маркова является неприводимой, периодической с периодом, равным N.
Некоторый j-тый класс (j 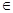 {1,2,…, N}) соответствует поступлению некоторого фиксированного маркера на j-тую АС. Вероятности переходов из j-того периодического класса в (j+1) – ый образуют (
{1,2,…, N}) соответствует поступлению некоторого фиксированного маркера на j-тую АС. Вероятности переходов из j-того периодического класса в (j+1) – ый образуют (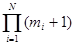
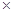
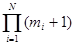 ) матрицу.
) матрицу.
Закодируем состояния КЛВС парами чисел (i, r), i=(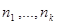 ), 0
), 0 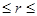
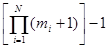 .Здесь i определяет класс состояний, т.е. равно номерам тех станций, на которых находятся маркеры, r определяет номер состояния.
.Здесь i определяет класс состояний, т.е. равно номерам тех станций, на которых находятся маркеры, r определяет номер состояния.
Введем обозначение M=(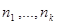 ) – множество номеров тех станций, на которых находятся маркера, R=(
) – множество номеров тех станций, на которых находятся маркера, R=(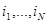 ),
), 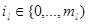 , l
, l 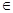 {1,…, N},
{1,…, N}, 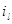 - обозначает количество сообщений на l-той АС. Также обозначим через P(
- обозначает количество сообщений на l-той АС. Также обозначим через P(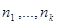 ) – вектор-строку вероятностей состояний КЛВС.
) – вектор-строку вероятностей состояний КЛВС.
Обозначим через 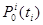 - вероятность того, что за время
- вероятность того, что за время 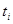 на i-тую АС не поступит ни одного сообщения;
на i-тую АС не поступит ни одного сообщения; 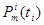 - вероятность того, что за время
- вероятность того, что за время 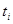 на i-тую АС поступит m сообщений;
на i-тую АС поступит m сообщений; 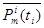 - вероятность того, что за время
- вероятность того, что за время 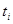 на i-тую АС поступит m и более сообщений.
на i-тую АС поступит m и более сообщений.
Так как поток сообщений пуассоновский, то имеем:
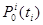 =
= 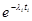
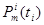 =
= 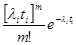
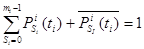 , i
, i 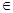 {1,2,…, N}
{1,2,…, N}
Изучая поведение КЛВС во вложенные Марковские моменты, получим следующую процедуру определения стационарных вероятностей сети.
Теорема. Стационарные вероятности рассматриваемой КЛВС вычисляются из соотношений:
|
|
|
P(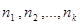 )=P(
)=P(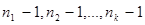 ) A(
) A(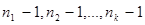 ;
; 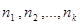 )
)
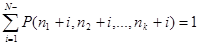 (1)
(1)
где А - 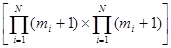 матрица вероятностей переходов из i-того периодического класса в состояние (i+1) – го класса, элементы которой вычисляются по формуле:
матрица вероятностей переходов из i-того периодического класса в состояние (i+1) – го класса, элементы которой вычисляются по формуле:
a(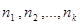 )=
)= 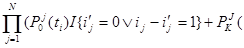
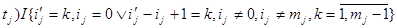 +
+ 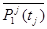
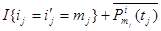
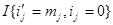 +
+ 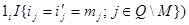 , времена вычисляются по следующим формулам:
, времена вычисляются по следующим формулам:
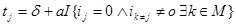
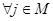
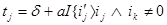
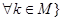
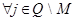
а также вероятность перехода равна нулю, если:
1)  >0
>0 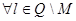 , Q={1,2,3,…, N}
, Q={1,2,3,…, N}
2) 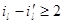
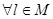
Доказательство:
P(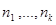 ) – вектор-строка вероятностей состояний i-того периодического класса; матрица А размерности
) – вектор-строка вероятностей состояний i-того периодического класса; матрица А размерности 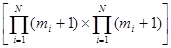 , элементами которой являются вероятности переходов из i-того периодического класса в (i+1) – ый.
, элементами которой являются вероятности переходов из i-того периодического класса в (i+1) – ый.
Вследствие периодичности цепи Маркова 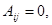 если
если 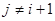 либо (i, j)
либо (i, j) 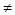 (N, 1). Из этих рассуждений имеем Р(1)=Р(N)
(N, 1). Из этих рассуждений имеем Р(1)=Р(N) 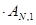
Р(J)=P (J-1) 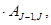 J
J 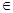 {2,3,…, N}, J определяет периодический класс.
{2,3,…, N}, J определяет периодический класс.
J определяет те, станции на которых находятся маркеры в данном периодическом классе, с учетом постановки математической модели любой маркер может переходить только на соседнюю станцию. Это и обуславливает то, что маркер с N-ной станции переходит на первую АС.
Таким образом, учитывая условие нормировки, имеем процедуру (1) определения векторов стационарных вероятностей КЛВС.
Доказано.
Для обоснования правильности формул времени необходимо учитывать следующие положения:
1) если поступает сообщение, а соответствующий буфер занят полностью, то сообщение теряется, и при подсчете поступивших сообщений оно не учитывается;
2) если сообщение не передается, то из данного буфера оно никуда не может исчезнуть, поэтому если при переходе из некоторого состояния в соседнее какое-то сообщение теряется, то вероятность данного перехода равна 0;
3) при передаче сообщения из АС, на которой есть маркер, буфер данной станции блокируется;
4) со станции с маркером может передаваться не более одного сообщения.
5) на тех станциях, на которых нет маркеров, может быть вероятность равна единице в том случае, если в i-том периодическом классе и в (i+1) – вом буфер станции был полностью занят.
|
|
|
2.2  Определение стационарных вероятностей состояний многомаркерной, несимметричной КЛВС с буферами
Определение стационарных вероятностей состояний многомаркерной, несимметричной КЛВС с буферами  , с 3 АС и 2-мя маркерами, с ординарной дисциплиной обслуживания
, с 3 АС и 2-мя маркерами, с ординарной дисциплиной обслуживания
Будем рассматривать поведение КЛВС в моменты поступления маркеров на АС. В этом случае изменение состояний КЛВС образуют конечную цепь Маркова.
Под состоянием КЛВС будем понимать состояние всех АС кольца в момент поступления на них маркеров. Каждая АС может находиться всегда в одном из 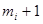 состоянии.
состоянии.
Все состояния КЛВС делятся на 3 периодических классов, каждый из которых содержит в рассматриваемом случае 12 состояний.
Особенности протокола приводят к тому, что указанная цепь Маркова является неприводимой, периодической с периодом, равным 3.
Некоторый j-тый класс (j 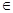 {1,2,3}) соответствует поступлению некоторого фиксированного маркера на j-тую АС. Вероятности переходов из j-того периодического класса в (j+1) – ый образуют
{1,2,3}) соответствует поступлению некоторого фиксированного маркера на j-тую АС. Вероятности переходов из j-того периодического класса в (j+1) – ый образуют  матрицу.
матрицу.
Закодируем состояния КЛВС парами чисел (i, r), i=(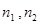 ), 0
), 0 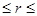 11. Здесь i определяет класс состояний, т.е. равно номерам тех станций, на которых находятся маркера, r определяет номер состояния.
11. Здесь i определяет класс состояний, т.е. равно номерам тех станций, на которых находятся маркера, r определяет номер состояния.
Введем обозначение M=(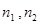 ) – множество номеров тех станций, на которых находятся маркера, R=(
) – множество номеров тех станций, на которых находятся маркера, R=(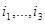 ),
), 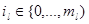 , l
, l 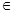 {1,2,3},
{1,2,3}, 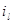 - обозначает количество сообщений на l-той АС. Также обозначим через P(
- обозначает количество сообщений на l-той АС. Также обозначим через P(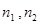 ) – вектор-строку вероятностей состояний КЛВС.
) – вектор-строку вероятностей состояний КЛВС.
Обозначим через 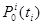 - вероятность того, что за время
- вероятность того, что за время 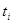 на i-тую АС не поступит ни одного сообщения;
на i-тую АС не поступит ни одного сообщения; 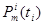 - вероятность того, что за время
- вероятность того, что за время 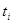 на i-тую АС поступит m сообщений;
на i-тую АС поступит m сообщений; 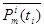 - вероятность того, что за время
- вероятность того, что за время 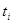 на i-тую АС поступит m и более сообщений.
на i-тую АС поступит m и более сообщений.
Так как поток сообщений пуассоновский, то имеем:
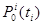 =
= 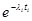
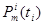 =
= 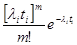
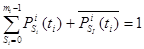 , i
, i 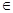 {1,2,3}
{1,2,3}
Изучая поведение КЛВС во вложенные Марковские моменты, получим следующую процедуру определения стационарных вероятностей сети, которая является частным случаем теоремы из пункта 2.1: стационарные вероятности рассматриваемой КЛВС вычисляются из соотношений:
P (2,3)=P (1,2) A (1,2);
P (3,1)=P (2,3) A (2,3);
P (1,2)=P (3,1) A (3,1);
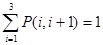
А – 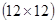 матрица вероятностей переходов из i-того периодического класса в состояние (i+1) – го класса, элементы которой вычисляются по формуле:
матрица вероятностей переходов из i-того периодического класса в состояние (i+1) – го класса, элементы которой вычисляются по формуле:
a(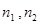 )=
)= 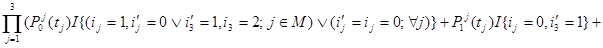
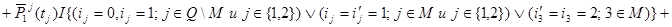
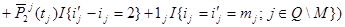
времена вычисляются по следующим формулам:
|
|
|
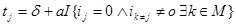
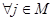
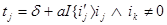
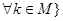
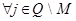
а также вероятность перехода равна нулю, если:
1) 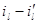 >0
>0 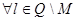 , Q={1,2,3}
, Q={1,2,3}
2) 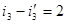
Для обоснования правильности формул времени необходимо учитывать следующие положения:
1) если поступает сообщение, а соответствующий буфер занят полностью, то сообщение теряется, и при подсчете поступивших сообщений оно не учитывается;
2) если сообщение не передается, то из данного буфера оно никуда не может исчезнуть, поэтому если при переходе из некоторого состояния в соседнее какое-то сообщение теряется, то вероятность данного перехода равна 0;
3) при передаче сообщения из АС, на которой есть маркер, буфер данной станции блокируется;
4) со станции с маркером может передаваться не более одного сообщения;
5) на тех станциях, на которых нет маркеров, может быть вероятность равна единице в том случае, если в i-том периодическом классе и в (i+1) – вом буфер станции был полностью занят.
В приложении будет предоставлены матрицы переходов для рассматриваемой КЛВС. Обозначение 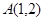 означает, что маркеры находились на первой и второй станциях.
означает, что маркеры находились на первой и второй станциях.
2.3 Определение стационарных вероятностей состояний многомаркерной, несимметричной КЛВС с буферами различной емкости, с N АС и k = N маркерами, с ординарной дисциплиной обслуживания
Будем рассматривать поведение КЛВС в моменты поступления маркеров на АС. В этом случае изменение состояний КЛВС образуют конечную цепь Маркова.
Под состоянием КЛВС будем понимать состояние всех АС кольца в момент поступления на них маркеров. Каждая АС может находиться всегда в одном из 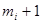
 состоянии.
состоянии.
Все состояния КЛВС делятся на N периодических классов, каждый из которых содержит в рассматриваемом случае 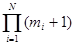 состояние.
состояние.
Особенности протокола приводят к тому, что указанная цепь Маркова является неприводимой, периодической с периодом, равным N.
Некоторый j-тый класс (j 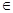 {1,2,…, N}) соответствует поступлению некоторого фиксированного маркера на j-тую АС. Вероятности переходов из j-того периодического класса в (j+1) – ый образуют (
{1,2,…, N}) соответствует поступлению некоторого фиксированного маркера на j-тую АС. Вероятности переходов из j-того периодического класса в (j+1) – ый образуют (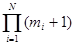

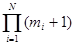 ) матрицу. Зафиксируем некоторый маркер и будем рассматривать поведение сети в моменты поступления этого маркера АС.
) матрицу. Зафиксируем некоторый маркер и будем рассматривать поведение сети в моменты поступления этого маркера АС.
|
|
|
Закодируем состояния КЛВС парами чисел (i, r), i=(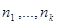 ), 0
), 0 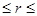
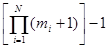 .Здесь i определяет класс состояний, т.е. равно номеру станции, на которой находятся маркеры, r определяет номер состояния.
.Здесь i определяет класс состояний, т.е. равно номеру станции, на которой находятся маркеры, r определяет номер состояния.
Введем обозначение M=(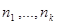 ) – множество номеров тех станций, на которых находятся маркера, R=(
) – множество номеров тех станций, на которых находятся маркера, R=(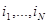 ),
), 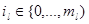 , l
, l 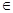 {1,…, N},
{1,…, N}, 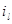 - обозначает количество сообщений на l-той АС. Также обозначим через P(
- обозначает количество сообщений на l-той АС. Также обозначим через P(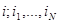 ) – вектор-строку вероятностей состояний КЛВС.
) – вектор-строку вероятностей состояний КЛВС.
Обозначим через 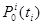 - вероятность того, что за время
- вероятность того, что за время 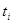 на i-тую АС не поступит ни одного сообщения;
на i-тую АС не поступит ни одного сообщения; 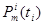 - вероятность того, что за время
- вероятность того, что за время 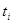 на i-тую АС поступит m сообщений;
на i-тую АС поступит m сообщений; 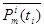 - вероятность того, что за время
- вероятность того, что за время 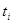 на i-тую АС поступит m и более сообщений.
на i-тую АС поступит m и более сообщений.
Так как поток сообщений пуассоновский, то имеем:
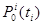 =
= 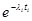
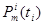 =
= 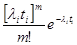
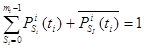 , i
, i 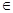 {1,2,…, N}
{1,2,…, N}
Изучая поведение КЛВС во вложенные Марковские моменты, получим следующую процедуру определения стационарных вероятностей сети, которую можно записать в виде:
P(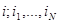 )=P(
)=P( ) A
) A 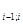
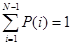
где А - 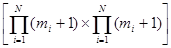 матрица вероятностей переходов из i-того периодического класса в состояние (i+1) – го класса, элементы которой вычисляются по формуле:
матрица вероятностей переходов из i-того периодического класса в состояние (i+1) – го класса, элементы которой вычисляются по формуле:
a(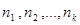 )=
)= 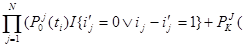
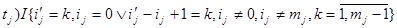 +
+ 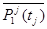
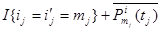
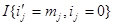 +
+ 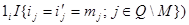 ,
,
времена вычисляются по следующим формулам:
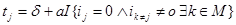
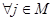
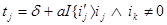
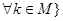
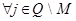
а также вероятность перехода равна нулю, если:
1) 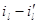 >0
>0 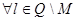 , Q={1,2,3,…, N}
, Q={1,2,3,…, N}
2) 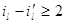
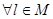
Для обоснования правильности формул времени необходимо учитывать следующие положения:
1) если поступает сообщение, а соответствующий буфер занят полностью, то сообщение теряется, и при подсчете поступивших сообщений оно не учитывается;
2) если сообщение не передается, то из данного буфера оно никуда не может исчезнуть, поэтому если при переходе из некоторого состояния в соседнее какое-то сообщение теряется, то вероятность данного перехода равна 0;
3) при передаче сообщения из АС, на которой есть маркер, буфер данной станции блокируется;
4) со станции с маркером может передаваться не более одного сообщения.
5) на тех станциях на которых нет маркеров может быть вероятность равна единице в том случае, если в i-том периодическом классе и в (i+1) – вом буфер станции был полностью занят.
|
|
|


