 |
II) Парадоксальность методики вычисления величины Э.Д.С. электромагнитной индукции.
|
|
|
|
Парадоксы теории электромагнетизма
I) Парадоксальность физической модели процесса распространения электромагнитных волн.
Как было изложено выше, распространение электромагнитных волн в пространстве осуществляется посредством взаимного преобразования изменяющегося во времени магнитного поля в электрическое, и изменяющегося во времени электрического поля в магнитное, что является основополагающим в идее электромагнетизма [1(в) т. 2 стр. 295], и определило электромагнитную природу световых и радиоволн. Однако если мы рассмотрим уравнения (1) и (2) системы уравнений электродинамики, то увидим, что для волнового решения данных уравнений, векторы E и B синфазны, т. е. энергия электрического поля и энергия магнитного поля одновременно проходят через максимум и через ноль, и, следовательно, никакого взаимного преобразования электрических и магнитных полей в пространстве и времени не происходит, что в корне противоречит самой идее электромагнетизма, как физической модели процесса распространения в пространстве электромагнитных волн. Из сказанного ясно, что в рамках электродинамики Максвелла никакой непротиворечивой физической модели процесса распространения в пространстве световых и радиоволн не существует, и природа их требует уточнения. Данную ситуацию нельзя назвать иначе, как парадоксальной.
II) Парадоксальность методики вычисления величины Э.Д.С. электромагнитной индукции.
Рассмотрим классическую методику определения величины Э.Д.С. электромагнитной индукции на примере расчета Э.Д.С. электромагнитной индукции на зажимах вторичной обмотки катушки индуктивности при протекании переменного тока в первичной обмотке катушки. Для решения этой задачи по классической методике предлагается следующая логика: под действием переменного тока, протекающего в первичной обмотке катушки индуктивности, внутри не╖ возникает переменный во времени поток вектора магнитной индукции B, а снаружи катушки, как следствие этого, возникает электрическое вихревое поле E. Под действием вихревого электрического поля E во вторичной обмотке катушки, размещенной в нем, течет электрический ток. Вектор плотности тока J определен согласно закону Ома в дифференциальной форме:
|
|
|
J = s E,
где s. электропроводность материала вторичной обмотки катушки.
Из дополнительного уравнения системы уравнений электродинамики имеем:

Подставим данное выражение вектора E в выражение для вектора J:
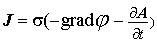
Разделив левую и правую части полученного выражения на " s ", получим:
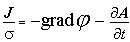
Но, т.к. вторичная обмотка катушки выполнена из металла, а электропроводность металлов очень велика, то при конечной плотности тока J напряженность электрического поля Е в проводнике вторичной обмотки катушки мала, и, следовательно, левую часть уравнения можно положить равной нулю.

И, следовательно:
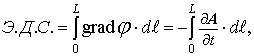
что и является искомым выражением для определения Э.Д.С. электромагнитной индукции, дающим результаты, точно совпадающие с экспериментом.
Из данной методики видно, что правильный результат получен за счет допущения равенства нулю вектора электрической напряженности E. Обоснованием этого допущения послужила высокая электропроводность металлической обмотки и конечная величина плотности тока, индуцированного в ней. Т.е., получение правильного выражения для Э.Д.С. электромагнитной индукции жестко привязано к величине проводимости материала вторичной обмотки и, следовательно, варьируя е╖, можно ожидать соответственного изменения величины Э.Д.С. электромагнитной индукции, чего не наблюдается на практике. В случае использования в качестве материала вторичной обмотки материалов с низкой электропроводностью задача вычисления Э.Д.С. электромагнитной индукции становится, очевидно, вообще не разрешимой, т.е. условие равенства нулю вектора электрической напряженности E является принципиальным для получения выражения Э.Д.С. электромагнитной индукции, дающего результаты, не противоречащие эксперименту. Но, как следует из предлагаемой физической модели процесса электромагнитной индукции, электрическая напряженность E является первопричиной поляризации проводника вторичной обмотки катушки, т.е. внешней воздействующей силой по отношению к ней и, следовательно, не может быть приравнена к нулю. Получение выражения для Э.Д.С. электромагнитной индукции, как реакции проводника вторичной обмотки катушки на воздействие электрического поля E, исходя из равенства вектора E нулю, вступает в неустранимое противоречие с третьим законом Ньютона и принципом причинности, что является парадоксом.
|
|
|
Из проведенного рассмотрения классической методики получения выражения для Э.Д.С. электромагнитной индукции следует, что в рамках электродинамики Максвелла не существует непротиворечивой физической модели, способной дать описание процессов электромагнитной индукции, а предлагаемый при╖м искусственен и приводит к неустранимым противоречиям с третьим законом Ньютона и принципом причинности.
Не трудно догадаться, что такое состояние физических моделей в классической электродинамике не могло не отразиться на формализации их в виде уравнений электродинамики.
При исследовании уравнений электродинамики и методов решения полевых задач, обнаруживается пренебрежение основными положениями классической теории поля (например, утверждение об условности разделения полей на потенциальные и вихревые), что имеет место во всех общеизвестных литературных источниках (см., например [1(а)]). В результате этого допускается произвол в методах решения полевых задач, появляются решения в виде виртуальных полей, и возникает необходимость введения дополнительных калибровочных соотношений, например: калибровка Лоренца, калибровка Кулона и т. д.[1;2], без какой.либо убедительной мотивации применения той или иной калибровки, что делает применение теории непосредственно в практической деятельности проблематичным.
|
|
|
На основании ранее сказанного, полагаю разумным, прежде чем перейти к исследованиям уравнений электродинамики Максвелла, уточнить основные понятия классической теории поля, такие как:
1) основная задача классической теории поля;
2) определение вектора поля в классической теории поля в общем виде;
3) действие дифференциальных операторов классической теории поля на вектор поля, заданный в общем виде;
|
|
|


