 |
Координаты вектора на плоскости и в пространстве.
|
|
|
|
Вектор. Основные понятия.
Вектор – направленный прямолинейный отрезок, т. е. отрезок, имеющий длину и определенное направление. Если 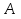 – начало вектора,
– начало вектора,  – его конец, то такой вектор обозначается как
– его конец, то такой вектор обозначается как  , или
, или  . Вектор
. Вектор  с началом в точке и концом в точке называется противоположным вектору и обозначается как
с началом в точке и концом в точке называется противоположным вектору и обозначается как  , или
, или 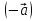 .
.
Длиной или модулем вектора называется длина отрезка  и обозначается
и обозначается  .
.
Вектор, длина которого равна нулю, называется нулевым вектором и обозначается как  . Считается, что он не имеет направления.
. Считается, что он не имеет направления.
Вектор, длина которого равна 1, называется единичным вектором и обозначается как 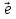 .
.
Векторы и  называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Это обозначается как
называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Это обозначается как  .
.
Линейные операции над векторами. Свойства линейных операций.
К линейным относятся операции сложения векторов и умножение вектора на число.
Суммой векторов 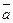 и
и  называется вектор, полученный по правилу сложения векторов:
называется вектор, полученный по правилу сложения векторов:
А) если совместить начала векторов, то суммой будет вектор, начало которого совпадает с началами векторов, а конечная точка- противоположная вершина параллелограмма, сторонами которого будут 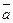 и
и  ;
;
В) если совместить начало второго вектора и конечную точку первого, то сумма – вектор, начало которого совпадает с начальной точкой первого вектора, а конечная – с конечной точкой второго.
Суммой конечного числа векторов служит замыкающий вектор:
Вектор 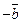 называется противоположным вектору
называется противоположным вектору  , если их длины совпадают, а направления противоположны.
, если их длины совпадают, а направления противоположны.
Разностью векторов 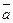 и
и  называется вектор
называется вектор  , который является суммой векторов
, который является суммой векторов 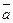 и -
и -  . Вектор
. Вектор  направлен к концу вектора
направлен к концу вектора 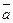 , если
, если 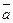 и
и  приведены к одному началу.
приведены к одному началу.
|
|
|
Произведением вектора 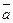 на число
на число  называется вектор
называется вектор  , для которого:
, для которого:
1) длина в  раз больше:
раз больше: 
2) направления совпадают, если  и противоположны, если
и противоположны, если 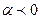
Для любого ненулевого вектора  можно определить орт вектора:
можно определить орт вектора:

Введенные операции называются линейными и обладают рядом свойств:
1) Сложение векторов коммутативно: 
2) Сложение векторов ассоциативно: 
3) 
4) 
5) Умножение вектора на число ассоциативно: 
Проекция вектора на ось.
Числовой осью называют прямую, на которой определено:
1. направление (→);
2. начало отсчета (точка О);
3. отрезок, который принимают за единицу масштаба
4.  .
.
Проекцией вектора на ось называется длина отрезка  этой оси, который расположен между основаниями проекций начала и конца вектора на ось. Она берется со знаком плюс, если направление отрезка совпадает с направлением оси проекций, и со знаком минус, если эти направления противоположны. Обозначение:
этой оси, который расположен между основаниями проекций начала и конца вектора на ось. Она берется со знаком плюс, если направление отрезка совпадает с направлением оси проекций, и со знаком минус, если эти направления противоположны. Обозначение:  .
.

Углом между вектором и осью называется угол  , на который необходимо кратчайшим образом повернуть ось, чтобы она совпадала с направлением вектора.
, на который необходимо кратчайшим образом повернуть ось, чтобы она совпадала с направлением вектора.
Свойства проекций:
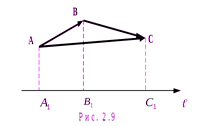
- равные векторы имеют равные проекции;
- при умножении вектора на число
 его проекция на ось также умножается на то же число;
его проекция на ось также умножается на то же число;
- проекция суммы двух векторов на ось равна сумме проекций этих векторов.
Координаты вектора на плоскости и в пространстве.
Изобразим декартову прямоугольную систему координат и от начала координат отложим единичные векторы  и
и  :
:

Векторы  и
и  ортогональны. Ортогональны = Перпендикулярны.
ортогональны. Ортогональны = Перпендикулярны.
Рассматриваемые векторы называют координатными векторами или ортами. Данные векторы образуют базис на плоскости. Базис и начало координат задают всю систему – это своеобразный фундамент, на котором кипит полная и насыщенная геометрическая жизнь.
Иногда построенный базис называют ортонормированным базисом плоскости: «орто» – потому что координатные векторы ортогональны, прилагательное «нормированный» означает единичный, т.е. длины векторов базиса равны единице.
|
|
|
Обозначение: базис обычно записывают в круглых скобках, внутри которых в строгой последовательности перечисляются базисные векторы, например:  . Координатные векторы нельзя переставлять местами.
. Координатные векторы нельзя переставлять местами.
Любой вектор  плоскости единственным образом выражается в виде:
плоскости единственным образом выражается в виде:
 , где
, где  – числа, которые называются координатами вектора в данном базисе. А само выражение
– числа, которые называются координатами вектора в данном базисе. А само выражение  называется разложением вектора
называется разложением вектора  по базису
по базису  .
.
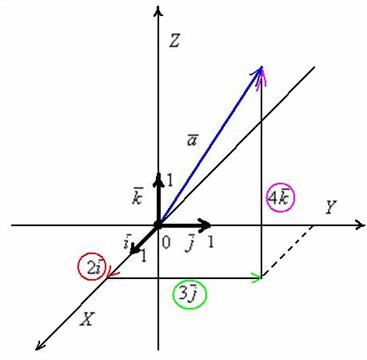
Ортонормированный базис  трехмерного пространства и прямоугольная система координат, единичные векторы
трехмерного пространства и прямоугольная система координат, единичные векторы  данного базиса попарно ортогональны:
данного базиса попарно ортогональны:  и
и  . Ось
. Ось  наклонена под углом 45 градусов только для того, чтобы складывалось визуальное впечатление пространства. Любой вектор
наклонена под углом 45 градусов только для того, чтобы складывалось визуальное впечатление пространства. Любой вектор  трехмерного пространства можно единственным способом разложить по ортонормированному базису
трехмерного пространства можно единственным способом разложить по ортонормированному базису  :
:
 , где
, где  – координаты вектора
– координаты вектора  (числа) в данном базисе.
(числа) в данном базисе.
Пример с картинки:  .
.
|
|
|


