 |
Понятие об уравнении линии на плоскости и в пространстве. Уравнение окружности.
|
|
|
|
Уравнением линии на плоскости в декартовой системе координат называют уравнение: F(х;у)=0, которому удовлетворяют координаты (х;у) любой точки этой линии и не удовлетворяют координаты ни одной точки, которые не принадлежат ей.
Линия в пространстве задаётся в общем случае как линия пересечения некоторых поверхностей S1 и S2.
Система уравнений:
называется уравнением линии в пространстве.
Окружностью называется линия, каждая точка М(х;у) на которой находится на одинаковом расстоянии 
от заданной точки 
, называемой центром окружности. Величина называется радиусом окружности.
В прямоугольной системе координат уравнение окружности имеет вид
,
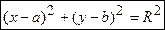где (a; b) — координаты её центра, 
— радиус окружности.
В частности, если центр окружности совпадает с началом координат, т.е. a=0, b=0, то уравнение окружности примет вид:
Уравнение прямой. Различные виды уравнений прямой.
Общее уравнение прямой:
1.
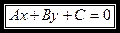, (2)
где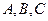 
— постоянные коэффициенты, причём 
и 
одновременно не обращаются в нуль 
.
Частные случаи этого уравнения:
— прямая проходит через начало координат;
— прямая параллельна оси 
;
— прямая параллельна оси 
;
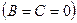— прямая совпадает с осью ;
— прямая совпадает с осью .
Нахождение углов между прямыми на плоскости. Условия параллельности и перпендикулярности прямых.
Если в пространстве заданы направляющий вектор прямой L
s = {l; m; n}
и уравнение плоскости
Ax + By + Cz + D = 0,
то угол между этой прямой и плоскостью можно найти используя формулу
| sinφ = | | A · l + B · m + C · n | |
| √A2 + B2 + C2 · √l2 + m2 + n2 |
Условия параллельности двух прямых:
а) Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:
|
|
|
k 1 = k 2.
б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.
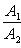
Условия перпендикулярности двух прямых:
а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.
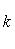
Это условие может быть записано также в виде
k 1 k 2 = -1.
б) Если уравнения прямых заданы в общем виде (6), то условие их перпендикулярности (необходимое и достаточное) заключается в выполнении равенства
A 1 A 2 + B 1 B 2 = 0.
Уравнение прямой в пространстве: параметрические и канонические.
Если прямая проходит через две точки A(x1, y1, z1) и B(x2, y2, z2), такие что x1 ≠ x2, y1 ≠ y2 и z1 ≠ z2, то уравнение прямой можно найти используя следующую формулу
| x - x1 | = | y - y1 | = | z - z1 |
| x2 - x1 | y2 - y1 | z2 - z1 | ||
Параметрические уравнения прямой могут быть записаны следующим образом
| x = l t + x0 |
| y = m t + y0 | |
| z = n t + z0 |
где (x0, y0, z0) - координаты точки лежащей на прямой, {l; m; n} - координаты направляющего вектора прямой.
Каноническое уравнение прямой в пространстве
Если известны координаты точки A(x0, y0, z0) лежащей на прямой и направляющего вектора n = {l;m; n}, то уравнение прямой можно записать в каноническом виде, используя следующую формулу
| x - x0 | = | y - y0 | = | z - z0 |
| l | m | n |
.
Уравнения плоскости.
Уравнение плоскости в прямоугольной системе координат Oxyz в трехмерном пространстве – это уравнение с тремя переменными x, y и z, которому удовлетворяют координаты любой точки заданной плоскости и не удовлетворяют координаты точек, лежащих вне данной плоскости.
|
|
|
Таким образом, уравнение плоскости обращается в тождество при подстановке в него координат любой точки плоскости. Если в уравнение плоскости подставить координаты точки, не лежащей в этой плоскости, то оно обратится в неверное равенство.
Всякое уравнение вида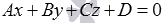 
, где A, B, C и D – некоторые действительные числа, причем А, В и C одновременно не равны нулю, определяет плоскость в прямоугольной системе координат Oxyz в трехмерном пространстве, и всякая плоскость в прямоугольной системе координат Oxyz в трехмерном пространстве может быть задана уравнением вида .
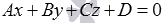Уравнение 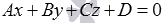называется общим уравнением плоскости в пространстве. Если не придавать числам А, В, С и D конкретных значений, то общее уравнение плоскости называют уравнением плоскости в общем виде.
|
|
|
