 |
Меры центральной тенденции
|
|
|
|
Представление выборки. Вариационный ряд
Понятия генеральной совокупности и выборки из нее являются первоначальными в статистике. Строгие определения пришли из теории вероятностей, хотя терминология математической статистики отличается от терминологии теории вероятностей. Вместо случайной величины X, ис-пользуемой в теории вероятностей, в математической статистике говорят о генеральной совокупности X. Таким образом, понятие генеральной совокупности тождественно понятию случайной величины, т.е. включает в себя описание области определения (пространства элементарных исходов), множества значений, функциональной зависимости, закона распределения.
Вместо эксперимента, в результате которого случайная величина X приняла значение х (в теории вероятностей), в математической статистике говорят о случайном выборе из генеральной совокупности X значения х. Вместо n независимых экспериментов, в результате которых случайная величина X приняла значения x1,x2,...,хn (в теории вероятностей), в математической статистике говорят о случайной выборке объема n значений x1,x2,..., хп из генеральной совокупности X.
При нестрогом подходе под генеральной совокупностью понимают множество всех объектов некоторого наблюдения в совокупности с множеством всех значений этого наблюдения, соответствующих каждому объекту. А под выборкой объема n понимают множество из n объектов, реально подвергшихся наблюдению, в совокупности с n значениями наблюдения для каждого объекта.
Например, социолог, изучающий мнение избирателей, под генеральной совокупностью понимает множество всех избирателей данной страны, а под выборкой объема n - множество из n человек, которых он опросил. Мы будем иметь в виду и такую точку зрения на генеральную совокупность.
|
|
|
Основная задача статистики - получить обоснованные выводы о свойствах генеральной совокупности, анализируя извлеченную из нее выборку x1,x2,...,хn.
Более подробно:
- описать закон распределения генеральной совокупности;
- подобрать значения параметров этого закона;
- оценить числовые характеристики генеральной совокупности;
- если генеральная совокупность - многомерная случайная величина, оценить всевозможные коэффициенты корреляции между ее составляющими;
- если имеется несколько выборок, извлеченных из разных генеральных совокупностей, определить, одинаково они распределены или нет;
- одинаковы или нет определенные числовые характеристики этих генеральных совокупностей и т.д.
Все перечисленные вопросы сформулированы на языке теории вероятностей. Чтобы ответы на подобные вопросы соответствовали действительности, нужно уметь строить подходящие вероятностные модели для реальных ситуаций, а для этого представить выборку в подходящем для изучения виде. Возникает задача описания и представления выборки. Наконец, располагая сведениями о свойствах генеральной совокупности, можно предсказать свойства повторно извлеченных из нее выборок - сделать прогноз.
Этап первичной статистической обработки данной выборки включает в себя следующие задачи:
- организация данных;
- визуализация (удобное наглядное представление) данных с целью формирования рабочих гипотез;
- описание и анализ эмпирических распределений.
Небольшие выборки удобно представлять в виде таблицы, в которую записывают элементы выборки (они называются вариантами), расположенные в порядке возрастания. Такое представление называется вариационным рядом.
Точечные оценки параметров распределения
Меры центральной тенденции
|
|
|
Меры центральной тенденции отражают тенденцию развития, т. е. действие главных причин (факторов) на распределение изучаемого признака.
1. Выборочная средняя арифметическая (оценка математического ожидания теоретического распределения)
 (2.1)
(2.1)
2. Выборочная медиана. Для вычисления медианы используем вариационный ряд. Вычисление медианы производится по формуле
 (2.2)
(2.2)
(2.3)
3. Выборочная мода. Для вычисления моды используем интервальный ряд. Вычисление моды производится по формуле
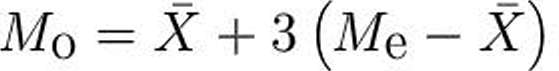
|
(2.4)
Выборочная медиана и мода относятся к классу порядковых статистик.
|
|
|


