 |
Рассчитаем и построим график амплитудного спектра радиоимпульсов.
|
|
|
|
Прежде чем приступать к расчету фильтра, необходимо определить частотный состав сигнала, поступающего на вход фильтра, т. е. рассчитать и построить график амплитудного спектра периодических радиоимпульсов.
Вначале находится несущая частота:

Затем рассчитываем частоты нулей огибающей спектра. Они зависят от длительности импульса:






Максимальное значение огибающей в виде напряжения, соответствующее частоте fн, находится по формуле:
 (1)
(1)
Зная максимальное значение и расположение нулей по оси частот, строим огибающую дискретного спектра периодических радиоимпульсов в виде пунктирной кривой в масштабе по оси частот (рис. 3).

Рис. 3
Внутри огибающей находятся спектральные составляющие или гармоники спектра с частотами fi, где i – номер гармоники. Они располагаются симметрично относительно несущей частоты, зависят от периода следования импульсов и находятся по формуле:
 .
.
Учитывая, что 
рассчитываем частоты гармоник, лежащих только справа от fн:


 и т.д.
и т.д.
Частоты гармоник, лежащих слева от fн:


 и т.д.
и т.д.
Амплитуды напряжения i -ых гармоник находятся по формуле:
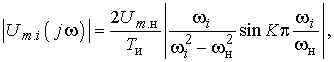 (2)
(2)
где количество периодов несущих колебаний косинусоидальной формы в импульсе K = t и/ T н =80/16= 5.





После расчета амплитуд по (2) их значения отражаются в виде дискретных составляющих внутри огибающей спектра.
2. Определяем частоты f п2 и f з2 и рассчитываем превышение амплитуды частоты f п2 над амплитудой частоты f з2 в децибелах в виде соотношения А ¢ = 20 lg Um п / Um з на входе фильтра.
Учитывая, что амплитуды спектральных составляющих на частотах 50 и 75 кГц равны нулю, примем за эффективную часть спектра, которую нужно выделить полосовым фильтром, диапазон частот от 53,9 кГц до 71,1 кГц. Следовательно, эти частоты будут определять частоты границы полосы пропускания фильтра f п1 и f п2 соответственно (рис. 4). Граничную частоту полосы непропускания f з2 выбираем равной частоте первой гармоники спектра сигнала, находящейся после частоты (f н + 1/ t и) = 75 кГц. Этой частотой является частота f 3 = 75,4 кГц. Следовательно, f з2 = f 3 = 75,4 кГц.
|
|
|
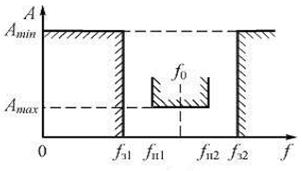
Рис. 4
Частоты fп1 и fп2 – границы ПП и частота fз2 – граница ПН справа; ослабление Аmin и Аmax = D А (рис. 4). Используя понятие центральной частоты или средней геометрической частоты ПП и ПН
 (3)
(3)
найдем центральную частоту ПП:

Тогда граничная частота fз.1 полосы непропускания будет:

Минимально-допустимое ослабление фильтра в ПН зависит от разницы амплитуд гармоник f2 и f3 спектра сигнала на выходе фильтра, выраженной в децибелах и заданной величиной Апол – полного ослабления:
 (4)
(4)
где  (5)
(5)
исходная разница амплитуд второй и третьей гармоник в децибелах, найденная в ходе расчета спектра радиоимпульсов.
Согласно формулы (2):
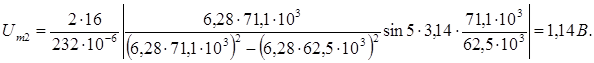

По формуле (5) находим:

3. Рассчитаем минимально допустимое ослабление фильтра в полосе задерживания А min = А пол – А ¢.
Из формулы (4):

Таким образом, требования к полосовому фильтру сводятся к следующему:




4. Рассчитаем порядок m НЧ-прототипа требуемого фильтра.
Требования к характеристикам ПФ пересчитываются в требования к его НЧ-прототипу:
 (6)
(6)
Используя формулу (6), находим граничные частоты ПП и ПН НЧ-прототипа:


Зная требования к ослаблению ФНЧ можно пересчитать их в требования к АЧХ ФНЧ или, как это принято в теории фильтров, в требования к квадрату АЧХ | H(j2 p f) |2 = | H(j w) |2. Для унификации расчетов вместо угловой частоты w вводят понятие нормированной частоты W = w / w н, где w н – нормирующая частота. Обычно в качестве w н выбирают граничную частоту ПП ФНЧ. Тогда:
 (7)
(7)
|
|
|
По формулам (7) получаем значения нормированных частот:

Требования к НЧ-прототипу могут быть проиллюстрированы рис. 5:

Рис. 5
При синтезе ФНЧ используются универсальные соотношения:
 (8)
(8)
 (9)
(9)
где y (W) – функция фильтрации; e – коэффициент неравномерности ослабления в ПП. Если в качестве y (W) используются полиномы, то фильтры называются полиномиальными. Среди последних наиболее широкое применение нашли фильтры Баттерворта и Чебышева.
Находим коэффициент неравномерности ослабления фильтра в ПП из рассмотрения (9) при A =ΔA и W = 1, когда y(1) = Тm(1) = 1:

|
|
|


