 |
Получим выражение для передаточной функции НЧ-прототипа при аппроксимации его характеристики полиномом Чебышева.
|
|
|
|
Порядок фильтра Чебышева находится также из рассмотрения (9), но при A = Amin и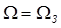 
, т. е. ослабление рассматривается в полосе непропускания. А в ПН полином Чебышева Тm(Ω) = ch m arch Ω, поэтому
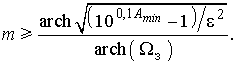(10)
Для вычисления функции archх рекомендуется соотношение:
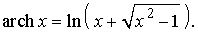
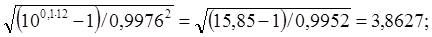
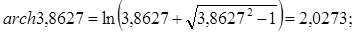
После подстановки в формулу (10) исходных данных и вычислений получим m = 2,26. Расчетное значение m необходимо округлить в бóльшую сторону до целого числа. В данном примере принимает m = 3.
Таблица 1
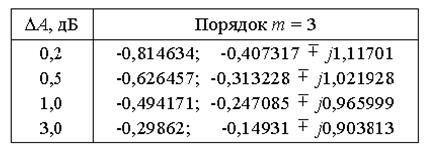
Пользуясь таблицей 1, находим полюсы нормированной передаточной функции НЧ-прототипа:
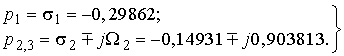(11)
Полюсы расположены в левой полуплоскости комплексной переменной р.
Формируем нормированную передаточную функцию НЧ-прототипа в виде:
где w (р) – полином Гурвица, который можно записать через полюсы:
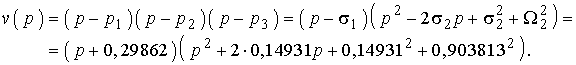
Производя вычисления, получим:
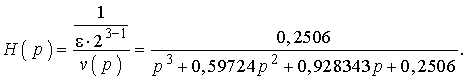(12)
Числитель равен свободному члену полинома знаменателя.
6. Осуществляем реализацию двухсторонне нагруженного полосового LC -фильтра.
Если фильтр со стороны зажимов 1–1¢ рассматривать как двухполюсник, образованный реактивным четырехполюсником и нагрузкой Rн (рис. 2), то, можно оперировать понятием входного сопротивления Zвх.1(р) двухполюсника со стороны зажимов 1–1¢:
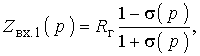(13)
где s (р) – коэффициент отражения, характеризующий несогласованность между сопротивлениями Rг и Zвх.1(р). Если известно Zвх.1(р), то двухполюсник можно реализовать, например, методом Дарлингтона. Один из возможных вариантов реализации схемы названным методом сводится к следующему. Осуществляют нормирование Zвх.1 по сопротивлению, выбирая в качестве нормирующего, сопротивление Rг, а коэффициент отражения записывают через табулированный полином h(р): s (р) = h(р)/v(р). Тогда (13) записывают как:
|
|
|
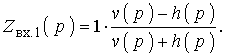(14)
Для фильтров Чебышева третьего порядка сам полином Чебышева равен:
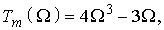(15)
а полином h(р) будет:
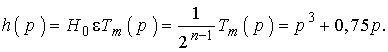(16)
Подставляя h(р) и v(р), записывают Zвх.1(р) в виде цепной дроби и по ней составляют схему двухполюсника, т. е. LC- фильтра нижних частот, нагруженного на сопротивление Rн. Элементы этой схемы представлены величинами, нормированными по частоте и по сопротивлению. Поэтому следующей операцией расчета является операция денормирования значения элементов НЧ-прототипа. После этого, используя формулы преобразования частоты, переходят от схемы НЧ-прототипа к схеме полосового фильтра. Элементы схемы ПФ, очевидно, будут иметь сразу реальные значения.
Подставляя в формулу (14) значение v(р) из формулы (12) и значение h(p) из формулы (16), после преобразований получим:
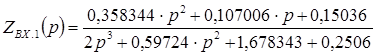(17)
Формула (17) описывает входное сопротивление двухполюсника (согласно схеме на рис.2, фильтр, нагруженный на сопротивление Rн, это действительно двухполюсник). А если известно выражение для входного сопротивления, то можно построить схему двухполюсника, воспользовавшись, например, методом Кауэра. По этому методу формула для Zвх(р) разлагается в непрерывную дробь путем деления полинома числителя на полином знаменателя. При этом степень числителя должна быть больше степени знаменателя. Исходя из последнего, формула (17) преобразуется к виду:
(18)
после чего производится ряд последовательных делений.
Вначале числитель делим на знаменатель:
Затем первый делитель делим на первый остаток:
Второй делитель делим на второй остаток:
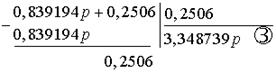
Третий делитель делим на третий остаток:
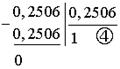
Получили четыре результата деления, которые отражают четыре нормированных по частоте и по сопротивлению элемента схемы в виде значений их проводимостей: pC, 1/pL, 1/R. Из анализа первого результата деления следует, что он отражает емкостную проводимость, поэтому все выражение (18) можно записать в виде цепной дроби:
|
|
|
(19)
По формуле (19) составляем схему (рис. 6), на которой С1н = 5,581; L2н = 0,427; С3н = 5,581; Rг.н = Rн.н = Rнор.
Рис. 6
Денормируем элементы схемы НЧ-прототипа, используя соотношения:
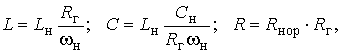(20)
где ωн = ωп.нч – нормирующая частота;
Rг – нормирующее сопротивление, равное внутреннему сопротивлению источника сигнала.
Используя соотношения (20) и значения ωн и Rг, получаем реальные значения элементов схемы НЧ-прототипа:
|
|
|
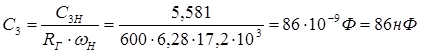
