 |
Расчет элементов схемы фильтра
|
|
|
|
В качестве типовой выбираем простейшую схему ПФ на одном операционном усилителе (ОУ) (рис. 8). Если составить эквивалентную схему, заменив ОУ ИНУНом, то, используя любой из методов анализа цепей, можно получить передаточную функцию, описывающую работу схемы на рис. 8, в виде:
 (29)
(29)
Из (29) видно, что рассмотренная схема является схемой второго порядка. Следовательно, для реализации функции (28) потребуется три подобных схемы или три звена, соединенных каскадно. Расчет элементов этих схем R1; R2; С3; С4; R5 ведется путем сравнения идентичных коэффициентов в формулах (28) и (29).
Для первого звена ПФ берутся коэффициенты из первого сомножителя (28):
 (30)
(30)
В системе (30) пять неизвестных и только три уравнения. Система нерешаема. Поэтому рекомендуется задаваться значениями, например, емкостей конденсаторов С3 и С4 (в ходе настройки фильтра при его изготовлении принято использовать переменные сопротивления, т. к. переменных конденсаторов с большой емкостью нет вообще).
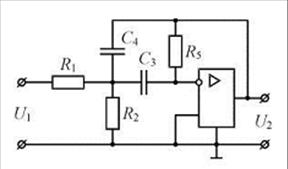
Рис. 8
Если принять С3 = С4 = 2 нФ, то, решая (30), получим:
R1 = 7,35 кОм, R5 = 31 кОм, R2 = 54 Ом.
Составляя аналогичную систему для второго звена, получим:
R1 = 7,35 кОм, R5 = 71,7 кОм, R2 = 31 Ом.
Аналогично для третьего звена:
R1 = 7,35 кОм, R5 = 54,6 кОм, R2 = 22,8 Ом.
Рассчитанные сопротивления не соответствуют стандартным номиналам резисторов. Поэтому для сопротивлений R1 и R5 в каждом звене берутся резисторы с номиналом, ближайшим к рассчитанному значению. Сопротивление R2 берется составным, из последовательно соединенных постоянном и переменном резисторов, что позволит осуществлять общую настройку фильтра.
8. Приведем ожидаемую характеристику ослабления полосового фильтра в зависимости от частоты, т. е. A = K (f).
|
|
|
При синтезе активного ПФ известна передаточная функция одного звена уже самой схемы фильтра (29). Очевидно, что Н(р) всего фильтра будет
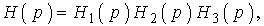 (31)
(31)
где значения каждого сомножителя будут отличаться из-за разницы в значениях сопротивлений звеньев фильтра. Формула (31) позволяет реализовать второй вариант проверки выполненных расчетов.
С этой целью в (29) производится замена переменной вида р = jω, в результате чего получаем выражение:
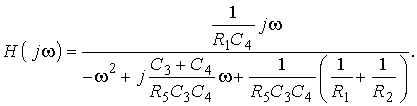
Находится модуль H(jω) в виде:
 (32)
(32)
Зная H(ω), легко найти зависимость ослабления от частоты вначале каждого звена, а затем всего фильтра:
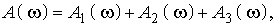 (33)
(33)
где,  (34)
(34)
В качестве числового примера выполним расчет первого звена фильтра.
Из предыдущих расчетов берем значения элементов:
С3 = С4 = 2 нФ; R1 = 7,35 кОм; R5 = 31 кОм; R2 = 54 Ом.
Подставляем эти значения в (32):

9. Рассчитаем ослабление ARC - фильтра на границах полосы пропускания и полосы непропускания (задерживания).

Первое звено. На частоте границы ПП f п2 = 71,1 кГц находим Н 1(ωп2) = 0,595:

Аналогично, на частоте границы ПН f з2 = 75,4 кГц находим Н 1(ω з2) = 0,426. Кроме того находим Н 1(ω) на частотах f п1 = 53,9 кГц и f з1 = 49,6 кГц.
Аналогичные расчеты выполняем для второго и третьего звеньев. Ослабления рассчитываем по формулам (33) и (34). Все результаты сводим в таблицу 4.
Таблица 4
| f з1 = 49,6кГц | f п1 = 53,9кГц | f п2 = 71,1кГц | f з2 = 75,4кГц | |
| H1(ω) H2(ω) H3(ω) | 0,393 1,2861 0,202 | 0,62 4,5967 0,264 | 0,595 0,35 3,59 | 0,426 0,288 1,325 |
| H(ω) | 0,102 | 0,752 | 0,747 | 0,162 |
| A1(ω) A2(ω) A3(ω) | 8,112 -2,185 13,89 | 4,152 -13,248 11,567 | 4,509 9,118 -11,102 | 7,412 10,812 -2,444 |
| A(ω) | 19,827 | 2,477 | 2,525 | 15,779 |
При анализе табличных данных обратим внимание на разный характер зависимости ослабления от частоты у разных звеньев фильтра. Если сравнивать рассчитанное ослабление всей схемы фильтра на частотах границ ПП и ПН с заданным ослаблением на этих же частотах, то можно сделать вывод о довольно хорошем их соответствии. При практическом изготовлении фильтров всегда предусматривается операция по их настройке, в ходе которой добиваются ослабления с требуемой точностью.
|
|
|
Приведем схему ARC -полосового фильтра.
На рис.9 приведена ожидаемая теоретическая кривая зависимости ослабления фильтра от частоты.
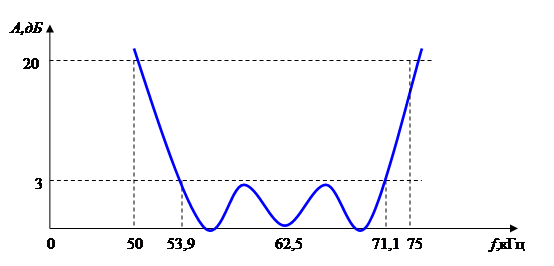
Рис. 9
На рис. 10 приведена принципиальная схема активного полосового фильтра.

Рис. 10
|
|
|


