 |
Методы учета фактора времени в финансовых операциях
|
|
|
|
Одним из важнейших свойств денежных потоков является их распределенность во времени. При анализе относительно краткосрочных периодов (до одного года) в условиях стабильной экономики данное свойство оказывает незначительное влияние, которым часто пренебрегают. Определяя годовой объем реализации по предприятию, просто складывают суммы выручки за каждый из месяцев отчетного года. Аналогично поступают со всеми остальными денежными потоками, что позволяет оперировать их итоговыми значениями. Однако в случае более длительных периодов или в условиях сильной инфляции возникает серьезная проблема обеспечения сопоставимости данных. Одна и та же номинальная сумма денег, полученная предприятием с интервалом в один и более год, в таких условиях будет иметь для предприятия неодинаковую ценность. В связи с этим возникает необходимость в разработке и совершенствовании методологии проведения финансовых вычислений.
Любая финансовая, кредитная или коммерческая операция представляет собой совокупность согласованных ее участниками следующих условий: сумма кредита (займа, инвестиций), цена товара, сроки и способы начисления процентов и погашения основного долга и т. д.
Учет фактора времени осуществляется с помощью методов наращения и дисконтирования, в основу которых положена техника процентных вычислений.
С помощью этих методов денежные суммы, относящиеся к различным временным периодам, приводят к требуемому моменту времени в настоящем или будущем. В качестве нормы приведения используется процентная ставка (interest rate ¾ r).
Под процентной ставкой в финансовых расчетах понимают абсолютную величину дохода от предоставления денег в долг в любой его форме. С помощью процентной ставки может быть определена как будущая стоимость «сегодняшних» денег, так и настоящая (современная, текущая или приведенная) стоимость.
|
|
|
Под наращением понимают процесс увеличения первоначальной суммы в результате начисления процентов.
Экономический смысл метода наращения состоит в определении величины, которая будет или может быть получена из некоторой первоначальной (текущей) суммы в результате проведения операции. Другими словами, метод наращения позволяет определить будущую величину (future value ¾ FV) текущей суммы (present value ¾ PV) через некоторый промежуток времени исходя из заданной процентной ставки r.
Операции наращения денег по процентной ставке более просты и понятны, так как с ними приходится сталкиваться довольно часто, беря или давая деньги взаймы. Однако большее значение имеет дисконтирование денежных потоков ¾ приведение их будущей стоимости к современному моменту времени для обеспечения сопоставимости величины распределенных по времени платежей.
В финансовом количественном анализе процентная ставка применяется не только как инструмент наращения суммы долга, но и как измеритель степени доходности (эффективности) финансовой операции вне зависимости от того, имел или не имел место непосредственный процесс передачи денежных сумм и нарастания суммы денег. Прирост стоимости измеряется в денежных единицах (например, в рублях) и обозначается I. Если обозначить будущую сумму S, а современную (или первоначальную) ¾ P, то I = S - P. Процентная ставка (r) является относительной величиной, измеряется в десятичных дробях или в процентах и определяется делением прироста стоимости на первоначальную сумму:

Можно заметить, что формула расчета процентной ставки идентична расчету статистического показателя «темп прироста». Действительно, если прирост стоимости (I) представляет собой прирост современной величины, то отношение этого прироста к самой современной величине и будет темпом прироста первоначальной суммы. Наращение первоначальной суммы по процентной ставке называется декурсивным методом начисления процентов.
|
|
|
Кроме процентной существует учетная ставка d (другое название ¾ ставка дисконта), величина которой определяется по формуле:
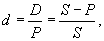
где D ¾ сумма дисконта.
Сравнивая формулы, можно заметить, что прирост стоимости I и величина дисконта D определяются одинаково ¾ как разница между будущей и современной стоимостью. Однако смысл, вкладываемый в эти термины, неодинаков. Если в первом случае речь идет о приросте текущей стоимости, своего рода «наценке», то во втором определяется снижение будущей стоимости, т. е. «скидка» с ее величины (diskont в переводе с немецкого означает «скидка»). Неудивительно, что основной областью применения учетной ставки является дисконтирование ¾ процесс, обратный по отношению к начислению процентов.
При помощи рассмотренных ставок могут начисляться как простые, так и сложные проценты. При начислении простых процентов наращение первоначальной суммы происходит в арифметической прогрессии, а при начислении сложных процентов ¾ в геометрической. Вначале более подробно рассмотрим операции с простыми процентами.
Рекомендация:
Обратитесь к примерам по указанным ссылкам: пример 35.1.1.
Продемонстрированная неравноценность двух одинаковых по величине (S 0= S 1= 10 000 руб.), но разных по времени получения ( ) денежных сумм ¾явление, широко известное и осознанное в финансовом мире. Его существование обусловлено целым рядом причин. Вот лишь некоторые из них:
) денежных сумм ¾явление, широко известное и осознанное в финансовом мире. Его существование обусловлено целым рядом причин. Вот лишь некоторые из них:
■ любая, имеющаяся в наличии денежная сумма, в условиях рынка может быть немедленно инвестирована и спустя некоторое время принести доход;
■ даже при небольшой инфляции покупательная способность денег со временем снижается;
■ предпочтение в общем случае индивидуумами текущего потребления будущему.
В зависимости от условий проведения финансовых операций, как наращение, так и дисконтирование могут осуществляться с применением простых, сложных либо непрерывных процентов.
|
|
|
Как правило, простые проценты используются в краткосрочных финансовых операциях, срок проведения которых меньше года. Базой для исчисления процентов за каждый период в этом случае является первоначальная (исходная) сумма сделки.
В общем случае наращение и дисконтирование по ставке простых процентов осуществляют по следующим формулам:

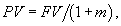
где r ¾ ставка процентов;
n ¾ число периодов.
Сложные проценты широко применяются в долгосрочных финансовых операциях ¾ со сроком проведения более одного года. Вместе с тем сложные проценты могут использоваться и в краткосрочных финансовых операциях, если это предусмотрено условиями сделки либо вызвано объективной необходимостью (например, высоким уровнем инфляции, риска). При этом база для исчисления процентов за период включает в себя как исходную сумму сделки, так и сумму уже накопленных к этому времени процентов.
Непрерывные проценты представляют главным образом теоретический интерес и редко используются на практике. Они применяются в особых случаях, когда вычисления необходимо проводить за бесконечно малые промежутки времени.
Методы наращения и дисконтирования играют важную роль в финансовом анализе, так как являются инструментарием для оценки потоков платежей.
Оценка потоков платежей
Проведение практически любой финансовой операции порождает движение денежных средств, которое может характеризоваться осуществлением, как отдельных платежей, так и множества выплат и поступлений, распределенных во времени.
В процессе количественного анализа финансовых операций удобно абстрагироваться от их конкретного экономического содержания и рассматривать порождаемые ими движения денежных средств как численный ряд, состоящий из последовательности распределенных во времени платежей: CF 0, CF1,..., Cfn. Для обозначения подобного ряда в мировой практике широко используется термин «поток платежей», или «денежный поток» (cash flow ¾ CF).
Отдельный элемент такого численного ряда (CFt) представляет собой разность между всеми поступлениями (притоками) денежных средств и их расходованием (оттоками) на конкретном временном отрезке проведения финансовой операции. В связи с этим величина CFt может иметь как положительный, так и отрицательный знак.
|
|
|
Количественный анализ денежных потоков, генерируемых за определенный период времени в результате реализации финансовой операции или функционирования каких-либо активов, в общем случае сводится к исчислению следующих характеристик:
FVn ¾ будущей стоимости потока за n периодов;
PVn ¾ современной стоимости потока за n периодов.
Часто возникает необходимость определения и ряда других параметров финансовых операций, важнейшими из которых являются:
CFt ¾ величина потока платежей в периоде t;
r ¾ процентная ставка;
n ¾ срок (количество периодов) проведения операции.
|
|
|


