 |
Системы эконометрических уравнений: виды, оценка параметров, область применения на практике
|
|
|
|
При использовании уравнений регрессии (линейных и нелинейных, парных и множественных) вида
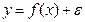7.1.1.
предполагалось, что y – случайная, а х – неслучайные (детерминированные) переменные. То есть, значения переменных х мы задаем, фиксируем, а затем наблюдаем получающиеся значения у. Данное допущение является одним из требований применения метода наименьших квадратов для оценки параметров уравнения регрессии, поскольку оно обеспечивает отсутствие корреляции регрессоров х и случайных ошибок регрессии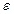 
и позволяет получить несмещенные и состоятельные оценки.
Если рассматривая модель содержит стохастические регрессоры, то оценки параметров, полученные методом наименьших квадратов:
- несмещенные и состоятельные, если объясняющие переменные и ошибки регрессии не коррелируют;
- состоятельные, но смещенные, если объясняющие переменные коррелируют с ошибками регрессии в более ранние моменты времени, но не коррелируют в один и тот же момент времени;
- смещенные и несостоятельные, если объясняющие переменные и ошибки регрессии коррелируют в том числе и в одинаковые моменты времени.
Одной из причин коррелированности регрессоров со случайными членами могут служить факторы, действующие одновременно и на сами регрессоры, и на объясняемые переменные при фиксированных значениях регрессоров. Значения объясняемых переменных и регрессоров в этом случае формируются одновременно под воздействием некоторых внешних факторов. Одна и та же переменная рассматривается как факторная, независимая, а с другой – как результативная, случайная величина.
Например, если существует зависимость:
|
|
|
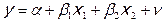7.1.2.
и одновременно
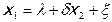, 7.1.3.
коэффициенты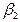 
и 
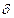значимо отличаются от нуля. Тогда в модели 7.1.1. факторы – коллинеарные. Если же рассматривать только модель:
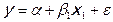, 7.1.4.
то возникает коррелированность регрессора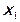 
и ошибок регрессии 
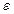, поскольку фактор 
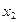действует одновременно и на у, и на 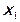, что приводит к смещенным и несостоятельным оценкам метода наименьших квадратов.
Поэтому естественным выходом из подобных ситуаций является построение не отдельных уравнений регрессии, а их систем, для оценивания которых применяются специальные методы (3 вопрос лекции).
Случайные переменные называют эндогенными, т.е. внутренними, так как они формируют свои значения внутри модели. Признаки, считающиеся заданными, известными, неслучайными получили название экзогенных, или внешних для данной системы. Один и тот же признак может быть эндогенным в одной задаче и экзогенным – в другой.
С точки зрения математической статистики, главное отличие между ними в том, что экзогенные переменные не коррелируют с ошибками регрессии. Если объединить в систему уравнения 7.1.1 и 7.1.2, эндогенными переменными будут у и х1, экзогенной – х2.
Далее будем обозначать экзогенные переменные х, а эндогенные – у.
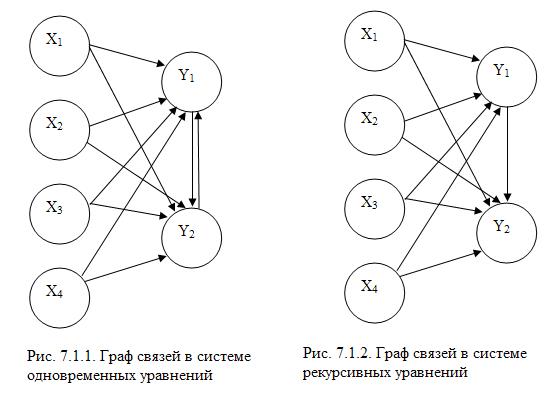
В зависимости от характера взаимосвязей между эндогенными и экзогенными переменными выделяют системы рекурсивных (рекуррентных) и совместных, одновременных, взаимосвязанных уравнений.
Если представить графически связи между переменными, то на рис. 7.1.1 представлен граф связей системы одновременных уравнений, на рис. 7.1.2 – рекурсивных.
Система одновременных уравнений в структурной форме:
|
|
|
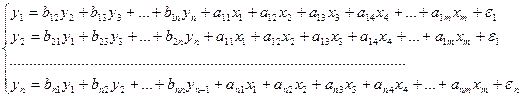(7.1.5)
Структурная форма модели содержит при эндогенных переменных коэффициенты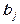 
, экзогенных переменных – 
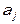, которые называются структурными коэффициентами модели. Все переменные в модели выражены в отклонениях от среднего уровня:
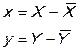7.1.6.
Поэтому свободные члены в системе отсутствуют.
Рис. 7.1.1 соответствует модель:
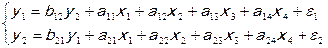7.1.7.
В общем виде модель системы рекурсивных уравнений будет иметь вид:
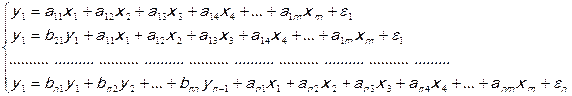7.1.8.
Рис. 7.1.2 соответствует модель:
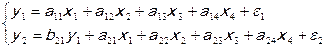7.1.9.
В системе рекурсивных уравнений хоты бы одна эндогенная переменная должна определятся только лишь набором независимых переменных. Если все эндогенные переменные расположены в левой части, а экзогенные – в правой, то такая система называется системой независимых уравнений. Для решения систем независимых и рекурсивных переменных используется метод наименьших квадратов.
Методы оценивания параметров систем одновременных уравнений рассмотрим далее.
7.1.2. Косвенный метод наименьших квадратов
Препятствие к применению метода наименьших квадратов, которое заключается в коррелированности эндогенных переменных со случайными членами легко преодолеть, если:
привести систему к виду, чтобы в правой части оставались только экзогенные переменные. Такая форма называется приведенной;
затем применить метод наименьших квадратов к каждому уравнению в приведенной форме и получить оценки ее параметров;
перейти от приведенной формы к структурной, проведя процедуру обратного преобразования параметров.
Эта методика получила название косвенного метода наименьших квадратов и позволяет получать состоятельные и несмещенные оценки параметров системы одновременных уравнений в структурной форме.
Проблема идентификации - Однозначности определения параметров структурной модели по приведенной формы. Переход необходим, поскольку экономический смысл и интерпретацию имеют только параметры структурной формы.
|
|
|
Структурный параметр называется идентифицируемым, если он может быть однозначно определен с помощью метода наименьших квадратов. Уравнение идентифицируемо, если идентифицируемы все входящие в него структурные параметры.
Структурный параметр называется неидентифицируемым, если его значение невозможно получить, даже зная точные значения параметров приведенной формы.
Структурный параметр называется сверхидентифицируемым, если косвенный метод наименьших квадратов дает несколько различных его оценок.
Модель:
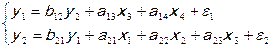7.1.30.
будет сверхидентифицируемой, поскольку по восьми коэффициентам приведенной формы нельзя однозначно определить семь – структурной формы.
Сверхидентифицируемая система в отличие от неидентифицируемой практически решаема, но не косвенным методом наименьших квадратов, а специальными методами.
Для проверки структурной модели на идентификацию, нужно проверить каждое уравнение системы:
1) модель считается идентифицируемой, если каждое уравнение системы идентифицируемо;
2) если хотя бы одно уравнение неидентифицируемо, то вся модель считается неидентифицируемой;
3) если в модели нет неидентифицируемых уравнений, но присутствует хотя бы одно сверхидентифицируемое, то модель – сверхидентифицируемая.
Условия идентифицируемости проверяются для каждого уравнения в отдельности. Чтобы уравнение было идентифицируемым, нужно, чтобы:
1+nx=ny (необходимое условие),
где nx – число экзогенных переменных, содержащихся в системе, но отсутствующих в данном уравнении системы;
ny – число эндогенных переменных в данном уравнении.
Если 1+nx<ny, уравнение неидентифицируемо;
1+nx>ny, то уравнение сверхидентифицируемо.
Применение
Наиболее широко системы одновременных уравнений применяются для моделирования макроэкономики. Большинство из них построено на основе кейнсианских моделей. Статическая модель Кейнса для описания народного хозяйства страны в наиболее простом варианте имеет следующий вид (в современных показателях системы национального счетоводства России):
|
|
|
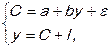7.2.1.
где С – конечное потребление в постоянных ценах;
у – валовой располагаемый национальный доход (ВРНД) в постоянных ценах;
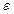– случайная составляющая;
I – валовые инвестиции в постоянных ценах (валовое сбережение).
Второе уравнение является тождеством, поэтому структурный коэффициент b не может быть больше 1. Он характеризует предельную склонность к потреблению. Так, если b=0,5, то из каждого дополнительного рубля дохода на потребление расходуется 50 копеек и 50 копеек инвестируется. Если b>1, то y < C+I – на потребление расходуются не только доходы, но и сбережения прошлых лет.
Система приведенных уравнений:
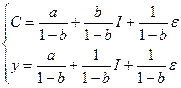7.2.2.
Приведенная форма модели содержит мультипликаторы:
- инвестиционный мультипликатор потребления:
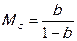; (7.2.3)
- инвестиционный мультипликатор национального дохода:
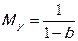. (7.2.4)
Мультипликаторы интерпретируются как коэффициенты линейной регрессии, т.е. они показывают, на сколько единиц изменится эндогенная переменная, если экзогенная переменная изменится на единицу.
Например, если b=0,5, то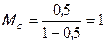 
. Из чего следует, что при росте инвестиций на 1 рубль, потребление так же увеличится на 1 рубль.
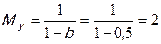, т.е. дополнительные инвестиции в размере 1 рубля приведут при прочих равных условиях к дополнительному росту чистого национального дохода на 2 рубля.
Кроме статических моделей широко применяются для моделирования экономики динамические модели. Динамическая модель Кейнса:
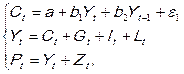(7.2.5)
где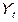 
– валовой располагаемый национальный доход;
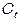– конечное потребление домашних хозяйств;
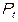– валовой национальный доход;
– (ВРНД) предыдущего года t;
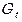– конечное потребление государственных учреждений;
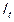– валовое накопление основного капитала;
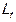– изменение запасов материальных оборотных средств и чистое приобретение ценностей;
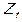– сальдо платежного баланса (чистые трансферты, полученные от «остального мира»).
Параметр а отражает влияние других, не учтенных факторов потребления. Первое уравнение является сверхидентифициуемым, второе и третье – тождествами.
Динамические модели обязательно содержат в правой части лаговые переменные. А также возможен учет тенденции, т.е. в модель может быть включен фактор времени. Например, модель Клейна в упрощенном варианте рассматривается как конъюнктурная модель:
|
|
|
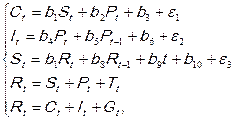(7.2.6)
где 
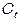– конечное потребление домашних хозяйств;
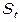– оплата труда наемных работников;
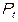– валовая прибыль и валовые смешанные доходы;
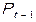– валовая прибыль и валовые смешанные доходы в предыдущий период;
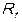– ВРНД;
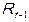– ВРНД в предыдущий период;
t – время;
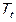– чистые трансферты и чистые доходы от собственности;
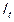– валовые инвестиции в постоянных ценах (валовое сбережение);
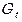– конечное потребление государственных учреждений.
Модель содержит пять эндогенных переменных, расположенных в левой част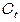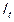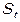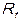и: – 
, , 
, 
и 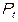, определяемую по первому тождеству; три экзогенные переменные – 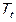, , 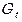t и две предопределенных, лаговых переменных – 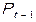и 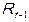. Как и большинство моделей такого типа, данная модель сверхидентифицируема и решается двухшаговым методом наименьших квадратов. Для интерпретации параметров и прогнозных целей используется, как и в модели Кейнса, приведенная форма модели:
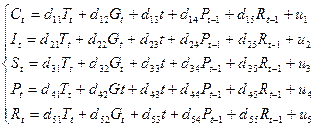(7.2.7)
Коэффициенты этой системы при обычных переменных 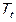и 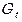являются мультипликаторами. Коэффициенты 
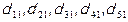– мультипликаторы чистых трансфертов (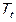) относительно конечного потребления домашних хозяйств (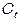), валового сбережения (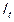), оплаты труда (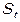), ВРНД (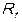) и валовой прибыли и валовых смешанных доходов (
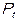). А коэффициенты 
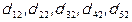являются мультипликаторами соответствующих эндогенных переменных.
Рассмотрим пример динамической модели открытой экономики с экономической активностью со стороны государства:
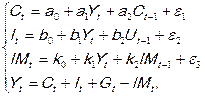(7.2.8)
где эндогенные переменные:
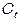– конечное потребление домашних хозяйств в период времени t;
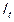– частные чистые инвестиции в отрасли экономики;
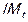– импорт;
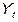– чистый располагаемый национальный доход.
Экзогенные предопределенные переменные:
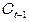– конечное потребление домашних хозяйств в предыдущий период времени;
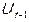– чистая прибыль и чистые смешанные доходы до налогообложения;
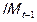– импорт за предыдущий период времени;
Экзогенная переменная 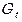– конечное потребление государственных учреждений плюс чистые капиталовложения в экономику страны (по этому же сектору) плюс изменение запасов минус чистые налоги плюс экспорт.
Первые три уравнения – сверхидентифицируемые, четвертое – тождество.
Системы эконометрических уравнений широко используются для моделирования спроса и предложения.
В простейшем виде модель спроса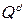 
и предложения 
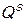может быть представлена следующим образом:
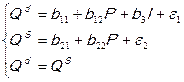(7.2.9)
Здесь I – доход. Рынок является равновесным: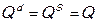 
. В этом случае P – цена равновесия, которая формируется одновременно со спросом и предложением. Следовательно, P и Q – эндогенные, а I – экзогенная переменная. Первое уравнение системы неидентифицируемо, чтобы практически реализовать эту модель следует изменить спецификацию и во второе уравнение ввести еще одну экзогенную переменную, например, налоги (N), которые выплачивают производители и продавцы. Если предположить, что исходные данные представлены временными рядами и величина налогов меняется со временем, то получим модель с учетом налога:
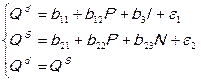(7.2.10)
Модель спроса и предложения в таком варианте точно идентифицируема и может быть решена косвенным методом наименьших квадратов.
|
|
|
