 |
Определение векторного пространства
|
|
|
|
Метод приведения к треугольному виду (метод Гаусса)
Напомним свойство 6 из элементарных свойств определителя: величина определителя не изменится если прибавить к любой его строке любую другую строку, умноженную на произвольную константу. Этот факт можно использовать для того, чтобы «сделать» в определителе побольше элементов равных нулю, т.к. содержащие эти элементы слагаемые выпадут из полного разложения определителя. Еще одно элементарное свойство — свойство 2, утверждает, что перестановка строк изменит знак определителя, но не изменит его абсолютную величину. Пользуясь этими двумя преобразованиями, можем поставить целью привести определитель к треугольному виду, т.е. к виду
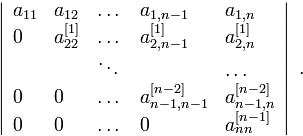
Формализовать приведение определителя к треугольному виду возможно с помощью используюшегося при решении систем линейных уравнений метода Гаусса. Так, первый шаг преобразования определителя

будет состоять в «обнулении» элементов первого столбца: из второй строки вычитается первая, домноженная на 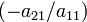 , из третьей строки — первая, домноженная на
, из третьей строки — первая, домноженная на 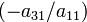 и т.д. Все эти операции не изменяют величины определителя, но преобразуют его к виду
и т.д. Все эти операции не изменяют величины определителя, но преобразуют его к виду

(при условии  ). Теперь можно разложить по первому столбцу и свести задачу к вычислению определителя порядка
). Теперь можно разложить по первому столбцу и свести задачу к вычислению определителя порядка 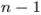 .
.
Перемножая элементы главной диагонали, получим определитель матрицы
Ссылка 1.2
Операции над векторами
Определение
Линейными операциями над векторами называются операции сложения векторов и умножения вектора на число.
Сложение и вычитание векторов
Определение
Сложение векторов 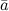 и
и  осуществляется по правилу треугольника.
осуществляется по правилу треугольника.
Суммой  двух векторов
двух векторов 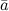 и
и  называют такой третий вектор
называют такой третий вектор 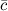 , начало которого совпадает с началом
, начало которого совпадает с началом 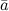 , а конец - с концом
, а конец - с концом  при условии, что конец вектора
при условии, что конец вектора 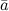 и начало вектора
и начало вектора  совпадают (рис. 1).
совпадают (рис. 1).
|
|
|
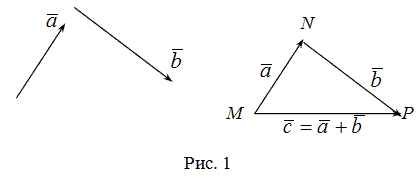
Для сложения векторов применяется также правило параллелограмма.
Определение
Правило параллелограмма - если два неколлинеарных вектора 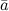 и
и  привести к общему началу, то вектор
привести к общему началу, то вектор  совпадает с диагональю параллелограмма, построенного на векторах
совпадает с диагональю параллелограмма, построенного на векторах 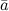 и
и  (рис. 2). Причем начало вектора
(рис. 2). Причем начало вектора 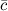 совпадает с началом заданных векторов.
совпадает с началом заданных векторов.

Вектор  называется противоположным вектором к вектору
называется противоположным вектором к вектору 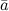 , если он коллинеарен вектору
, если он коллинеарен вектору 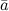 , равен ему по длине, но направлен в противоположную сторону вектору
, равен ему по длине, но направлен в противоположную сторону вектору 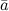 .
.
Операция сложения векторов обладает следующими свойствами:
1.  - коммутативность
- коммутативность
2.  - ассоциативность
- ассоциативность
3. 
4. 
Определение
Разностью 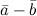 векторов
векторов 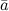 и
и  называется вектор
называется вектор 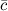 такой, что выполняется условие:
такой, что выполняется условие:  (рис. 3).
(рис. 3).

Умножение вектора на число
Определение
Произведением 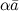 вектора
вектора 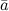 на число
на число  называется вектор
называется вектор  , удовлетворяющий условиям:
, удовлетворяющий условиям:
1. 
2. 
3.  , если
, если  ,
,  , если
, если  .
.
Свойства умножения вектора на число:
1. 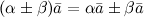
2. 
3. 
4. 
5. 
6. 
Здесь 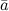 и
и  - произвольные векторы,
- произвольные векторы,  ,
,  - произвольные числа.
- произвольные числа.
Векторное пространство
Определение вектора
Вектором называется упорядоченное множество из  элементов поля, обозначаемое как
элементов поля, обозначаемое как  . Величины
. Величины  называются компонентами (координатами) вектора. Число компонентов вектора
называются компонентами (координатами) вектора. Число компонентов вектора  называется длиной вектора. Векторы считаются равными, если равны их соответствующие компоненты. Число ненулевых компонентов вектора называют весом вектора Сложение двух векторов длины
называется длиной вектора. Векторы считаются равными, если равны их соответствующие компоненты. Число ненулевых компонентов вектора называют весом вектора Сложение двух векторов длины  определяется следующим образом:
определяется следующим образом:
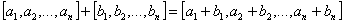 . .
|
Умножение элемента поля на вектор производится покомпонентно:
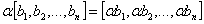 , ,
|
причем сложение и умножение компонентов векторов происходит по правилам сложения и умножения в поле  .
.
Для векторов введено понятие нормы [25, 33], которая для вектора 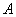 определяется как
определяется как  , где символ
, где символ 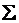 означает суммирование в поле действительных чисел. Если компоненты вектора принадлежат двоичному полю, тонорма вектора совпадает с числом его ненулевых компонентов, т.е. с его весом.
означает суммирование в поле действительных чисел. Если компоненты вектора принадлежат двоичному полю, тонорма вектора совпадает с числом его ненулевых компонентов, т.е. с его весом.
|
|
|
Вектор 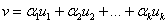 , где
, где  – элементы поля, называют линейной комбинацией векторов
– элементы поля, называют линейной комбинацией векторов  . Векторы
. Векторы  называются линейно зависимыми, если в
называются линейно зависимыми, если в  существуют такие элементы
существуют такие элементы  , по крайней мере один из которых не равен нулю, такие что
, по крайней мере один из которых не равен нулю, такие что  и линейно независимыми в противном случае. Если векторы линейно зависимы, то любой из них может быть выражен через линейную комбинацию остальных.
и линейно независимыми в противном случае. Если векторы линейно зависимы, то любой из них может быть выражен через линейную комбинацию остальных.
Определение векторного пространства
Множество  называется векторным пространством, если для него выполняются следующие аксиомы:
называется векторным пространством, если для него выполняются следующие аксиомы:
V. 1. Множество  является аддитивной абелевой группой.
является аддитивной абелевой группой.
V.2. Для любого вектора 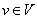 и любого скаляра – элемента
и любого скаляра – элемента  поля
поля  определено произведение
определено произведение  , являющееся вектором. Это произведение определено так, что
, являющееся вектором. Это произведение определено так, что  , где
, где  – единичный элемент поля
– единичный элемент поля  .
.
V.3. Выполняются законы дистрибутивности
 и и 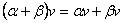 , ,
|
где  – скаляры, а
– скаляры, а  и
и  – векторы.
– векторы.
V.4. Выполняется закон ассоциативности
 , ,
|
где  – скаляры, а
– скаляры, а  – вектор.
– вектор.
|
|
|


