 |
Свойства скалярного произведения.
|
|
|
|
Для любых векторов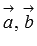 
и 
справедливы следующие свойства скалярного произведения:
1. свойство коммутативности скалярного произведения 
;
2. свойство дистрибутивности 
или 
;
3. сочетательное свойство 
или 
, где 
- произвольное действительное число;
4. скалярный квадрат вектора всегда не отрицателен 
, причем 
тогда и только тогда, когда вектор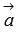 
нулевой.
Скалярным произведением двух векторов на плоскости или в трехмерном пространстве в прямоугольной системе координат называется сумма произведений соответствующих координат векторов формула и формула.
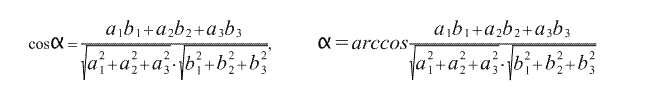
2.4
Три некомпланарных вектора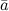 
, 
и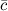 
, приведенных к общему началу, образуют так называемую связку трех векторов (или тройку векторов).
Тройка векторов называется упорядоченной, если четко сказано, какой вектор в ней идет первым, и так далее.
Тройка векторов 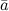, и 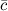называется левой, если поворот от вектора 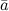к вектору , видимый с конца третьего вектора 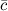, осуществляется по ходу часовой стрелки (рис. 1).
Тройка векторов 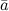, и 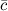называется правой, если поворот от вектора 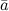к вектору , видимый с конца третьего вектора 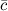, осуществляется против хода часовой стрелки (рис. 2).
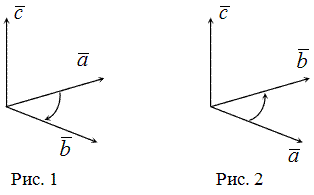
Геометрическая интерпретация скалярного произведения это длина проекции первого вектора на единичный вектор, задающий направления второго. Если два вектора перпендикулярны, скалярное произведение равно нулю.
2.5
2,5
Сме́шанноепроизведе́ние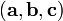 
векторов 
— скалярное произведение вектора 
на векторное произведение векторов 
и 
:
.
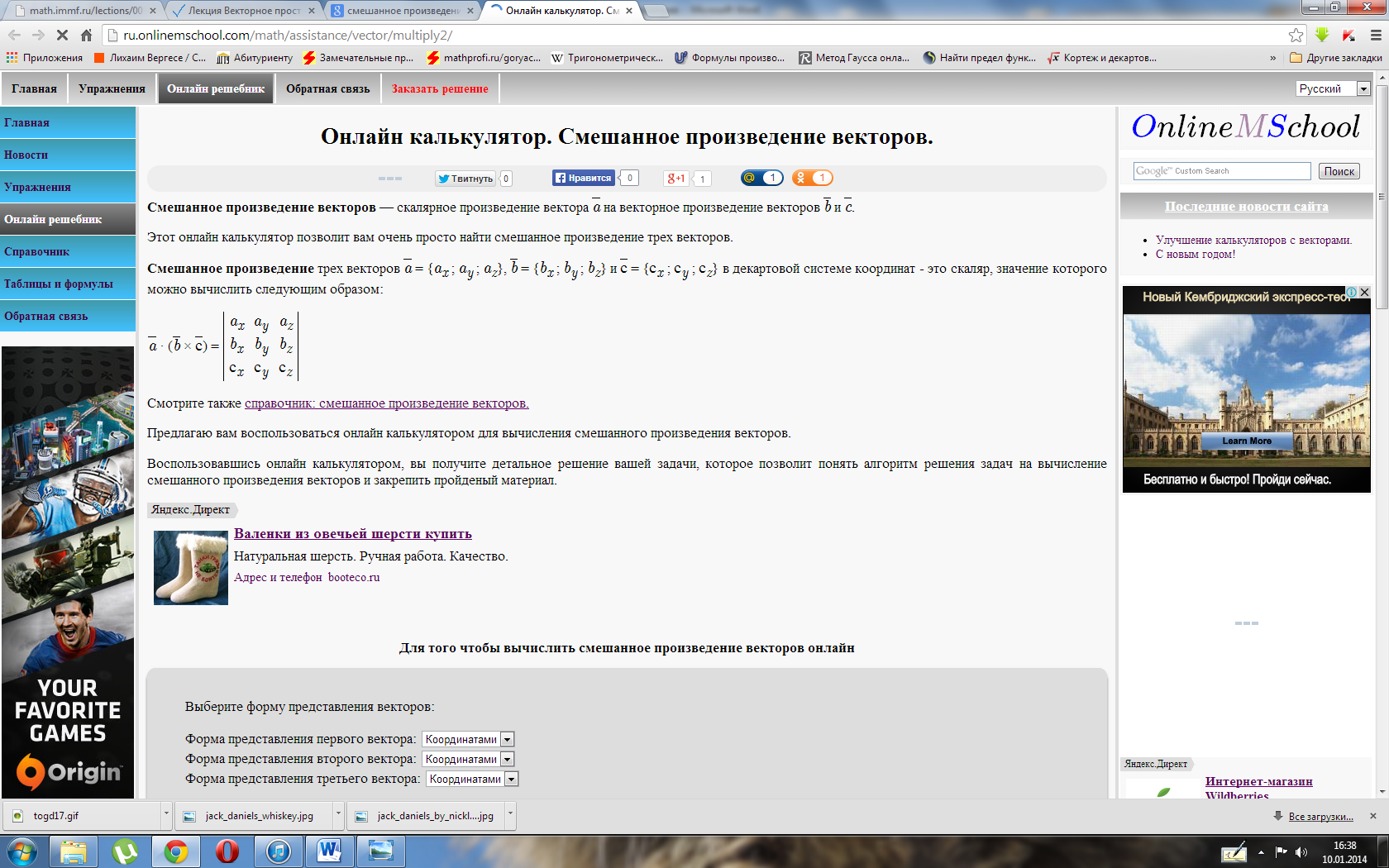
Геометрический смысл смешанного произведения: если тройка векторов 
правая, то их смешанное произведение равно объему параллелепипеда построенного на этих векторах: 
. В случае левой тройки смешанное произведение указанных векторов равно объему параллелепипеда со знаком минус: 
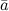. Если , и 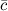компланарны, то их смешанное произведение равно нулю.
|
|
|
Итак, из выше сказанного можно сделать вывод, что объем параллелепипеда, построенного на векторах 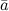, и 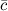равен модулю смешанного произведения этих векторов:
Объем пирамиды, построенной на этой тройке векторов равен
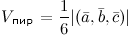
Свойства смешанного произведения:
1°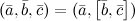 
2°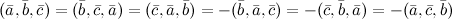 
3° Три вектора компланарны тогда и только тогда, когда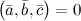 
4° Тройка векторов является правой тогда и только тогда, когда 
. Если же 
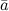, то векторы , и 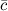образуют левую тройку векторов.
5°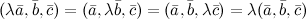 
6°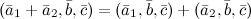 
7°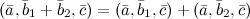 
8°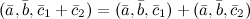 
9°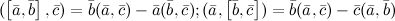 
10° Тождество Якоби: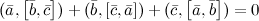 
Если векторы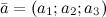 
, 
и 
заданы своими координатами, то их смешанное произведение вычисляется по формуле
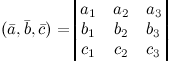
3,1
Угол между двумя прямыми
Угол φ между двумя прямыми, заданными общими уравнениями A1x + B1y + C1 = 0 и A2x + B2y + C2 = 0, вычисляется по формуле:
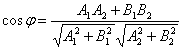
Угол φ между двумя прямыми, заданными каноническими уравнениями (x-x1)/m1 = (y-y1)/n1 и (x-x2)/m2 = (y-y2)/n2, вычисляется по формуле:
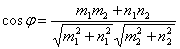
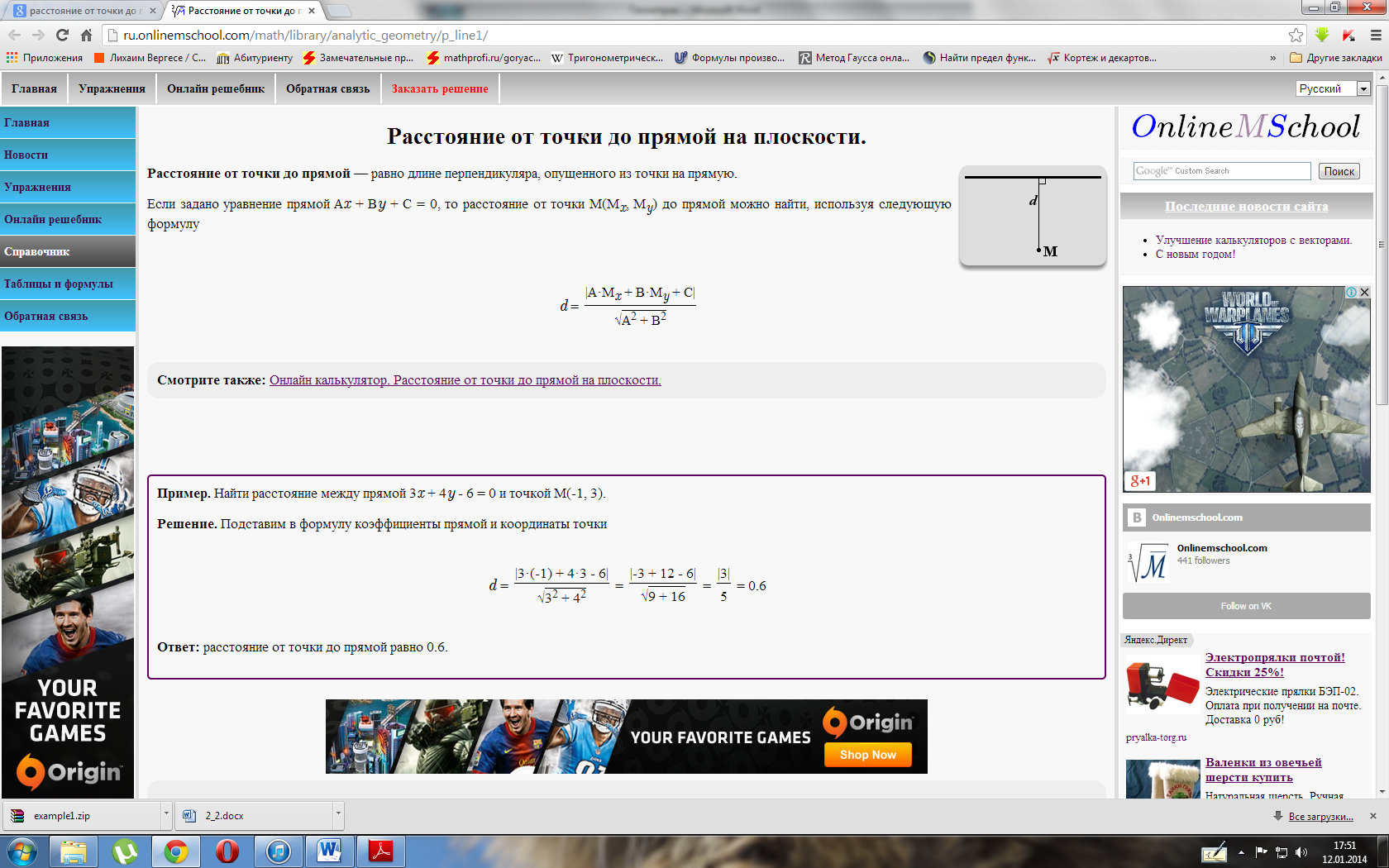
Расстояние от точки до прямой
3,2
Каждую плоскость в пространстве можно представить как линейное уравнение, называемое общим уравнением плоскости
,
Частные случаи.
o Если в уравнении (8) 
, то плоскость проходит через начало координат.
o При 
(
, 
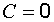) плоскость параллельна оси 
(оси 
, оси 
) соответственно.
o При 
(
, 
) плоскость параллельна плоскости 
(плоскости 
, плоскости 
).
· Даны точки 
, 
, 
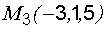. Составить уравнение плоскости 
.
Решение: используем (7)
,
.
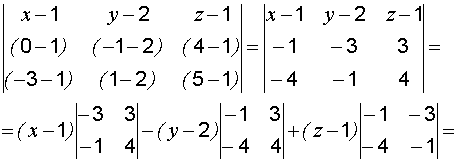
Ответ: общее уравнение плоскости 
.
· Пример.
Плоскость в прямоугольной системе координат Oxyz задана общим уравнением плоскости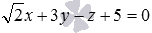 
. Запишите координаты всех нормальных векторов этой плоскости.
Решение.
Нам известно, что коэффициенты при переменных x, y и z в общем уравнении плоскости являются соответствующими координатами нормального вектора этой плоскости. Следовательно, нормальный вектор 
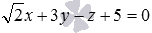заданной плоскости имеет координаты 
. Множество всех нормальных векторов можно задать как 
.
|
|
|
Ответ:
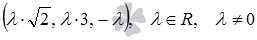
· Пример.
Напишите уравнение плоскости, если в прямоугольной системе координат Oxyz в пространстве она проходит через точку 
, а 
- нормальный вектор этой плоскости.
Решение.
Приведем два решения этой задачи.
Из условия имеем 
. Подставляем эти данные в общее уравнение плоскости, проходящей через точку 
:
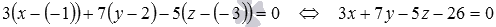
· Пример.
Напишите общее уравнение плоскости параллельной координатной плоскости Oyz и проходящей через точку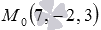 
.
Решение.
Плоскость, которая параллельна координатной плоскости Oyz, может быть задана общим неполным уравнением плоскости вида 
. Так как точка 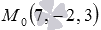принадлежит плоскости по условию, то координаты этой точки должны удовлетворять уравнению плоскости 
, то есть, должно быть справедливо равенство 
. Отсюда находим 
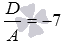. Таким образом, искомое уравнение имеет вид 
.
· Требуется написать уравнение плоскости, проходящей через точку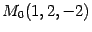 
и параллельной векторам 
и 
.
Решение. Векторное произведение 
по определению 10.26 ортогонально векторам p и q. Следовательно, оно ортогонально искомой плоскости и вектор 
можно взять в качестве ее нормального вектора. Найдем координаты вектора n:
то есть 
. Используя формулу (11.1), получим
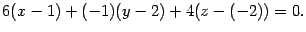
Раскрыв в этом уравнении скобки, приходим к окончательному ответу.
Ответ: 
.
· Найти единичный нормальный вектор плоскости 
.
Перепишем вектор нормали в виде 
и найдём его длину:
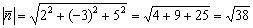
Согласно вышесказанному: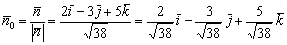 
Ответ: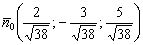 
· Построить плоскость, проходящую через точку 
параллельно плоскости 
.
У параллельных плоскостей один и тот же вектор нормали. 1) Из уравнения 
найдём вектор нормали плоскости: 
.
2) Уравнение плоскости 
составим по точке и вектору нормали :
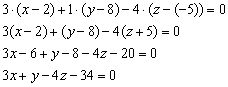
Ответ: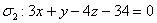 
Векторное уравнение плоскости в пространстве
Параметрическое уравнение плоскости в пространстве
|
|
|
