 |
Свойства векторного пространства
|
|
|
|
1. Максимальное число линейно независимых векторов в 
называется размерностью пространства над полем 
.
2. Совокупность 
любых линейно независимых векторов называется базисом и-мерного пространства, если каждый из векторов пространства может быть представлен в виде линейной комбинации этих векторов. Векторы совокупности называются базисными.
3. Подмножество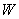 
векторного пространства такое, что любая линейная комбинация векторов этого подмножества снова принадлежит 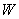, называется подпространством пространства . Легко проверить, что все векторы подпространства удовлетворяют аксиомам V.1 – V.4. Очевидно, что размерность подпространства не превышает размерности пространства, т.к. во всем пространстве содержится не более линейно независимых векторов. Каждое подпространство можно рассматривать как самостоятельное пространство. Следовательно, каждое подпространство имеет свой базис.
4. Скалярным произведением двух векторов одинаковой длины : 
и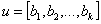 
называется скаляр, определяемый как
 .
|
Можно показать, что 
и 
.
Если скалярное произведение двух векторов равно нулю, то говорят, что эти векторы ортогональны. Два пространства называются взаимно ортогональными, если каждый вектор одного пространства ортогонален любому вектору другого пространства.
Множество всех векторов пространства , ортогональных подпространству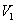 
, образуют подпространство 
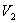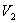пространства . Подпространство часто называют нулевым пространством для .
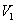Можно показать, что если 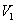– подпространство размерности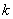 
-мерного векторного пространства , то размерность нулевого пространства равна 
.
5. Для векторного пространства определено понятие расстояния между двумя векторами, которое совпадает с нормой разности этих векторов
|
|
|
 ,
|
где суммирование производится в поле действительных чисел.
Определение линейной комбинации векторов:
Определение линейно зависимой системы векторов:
Определение линейно независимой системы векторов:
Необходимое и достаточное условие линейной зависимости векторов:
Система векторов векторного пространства является линейно зависимой тогда и только тогда, когда один из векторов системы линейно выражается через другие вектора этой системы.
Доказательство:
1) Необходимость:
Пусть элементы 
2) Достаточность:
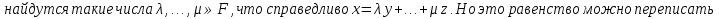
Теорема доказана.
Свойства (следствия):
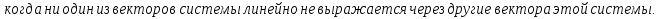
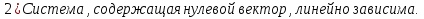
Доказательство:
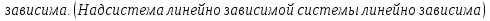
Доказательство:
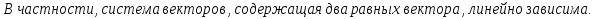
Доказательство:
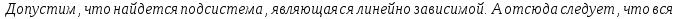
Определение полной системы векторов:
Свойства:
Доказательство:
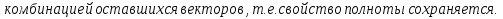
Доказательство:
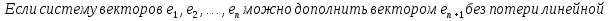
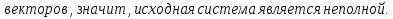
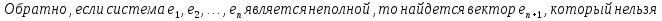
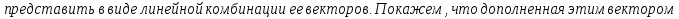
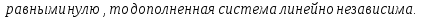
Определение базиса линейного пространства:
Единственность разложения по базису:
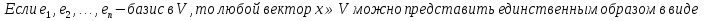
Доказательство:
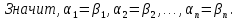
Размерность линейного пространства:
Определение. Система векторов называется максимальной линейно независимой системой, если она линейно независима и ее нельзя включить в большую линейно независимую систему в качестве подсистемы.
Существование максимальных линейно независимых систем. Возьмем любой вектор 
. Будем добавлять к нему векторы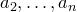 
, 
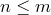так, чтобы все векторы были линейно независимы. Придем к максимальной системе за конечное число шагов.
Минимальная полная система векторов из V называется базисом пространства. Число векторов в базисе называется размерностью пространства.
2.2 В прямоугольной системе координат х0у проекции х и у вектора 
на оси абсцисс и ординат называются координатами вектора. Координаты вектора общепринято указывать в виде (х, у), а сам вектор как: =(х, у).
|
|
|
