 |
Формула парабол (Симпсона)
|
|
|
|
Лабораторная работа №1
ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Теоретическая часть
Пусть требуется вычислить определенный интеграл I = 
,
где f (x) – непрерывная на отрезке [ a, b ] функция. Если можно найти первообразную F (x) от функции f (x), то этот интеграл вычисляется с помощью формулы Ньютона-Лейбница: I = F (b) – F (a). Если же первообразная не является элементарной функцией, или функция f (x) задана графиком или таблицей, то формулой Ньютона-Лейбница воспользоваться уже нельзя. В этом случае определенный интеграл вычисляют приближенно. Приближенно вычисляют определенный интеграл и тогда, когда первообразная F (x) хоть и является элементарной функцией, но точные ее значения F (b) и F (a) получить не просто.
Приближенные методы вычисления определенного интеграла главным образом основаны на геометрическом смысле определенного интеграла: если f (x) ≥ 0, то интеграл I равняется площади криволинейной трапеции, ограниченной кривой у = f (x) и прямыми
х = а, х = b, y = 0.
Идея приближенного вычисления интеграла лежит в том, что заданная кривая у = f (x) заменяется новой линией, «близкой» к заданной. Тогда искомая площадь приближенно равна площади фигуры, ограниченной сверху этой линией.
Формула прямоугольников
Определение определенного интеграла как предела интегральных сумм
= 
,
не зависящих ни от выбора точек xk, k = 1, 2, …, n, разбиения отрезка [ a, b ] на частичные отрезки [ xk – 1, xk ], ни от выбора точек ξk, k = 1, 2, …, n, внутри этих отрезков (ξk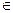 
[ xk – 1, xk ]) позволяет, во-первых, разбить отрезок на равные частичные отрезки, во-вторых, выбирать точки ξk удобным для вычислений образом.
 | |||||
 | |||||
 | |||||
|
|
|
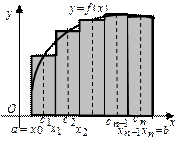
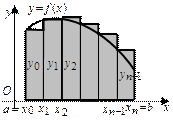
Рис.1. Рис.2. Рис.3.
Пусть требуется вычислить определенный интеграл от непрерывной на отрезке [ a, b ] функции f (x). Поделим отрезок [ a, b ] на n равных частей точками
xk = a + 
k, k = 0, 1, …, n,
и найдем значения функции f (x) в этих точках:
f (x 0) = у 0, f (x 1) = у 1, …, f (xn) = уn.
Заменим заданную криволинейную трапецию (рис.1) ступенчатой фигурой, которая состоит из n прямоугольников. Основания этих прямоугольников одинаковы и равны , а высоты совпадают со значениями уi в начальных точках частичных интервалов. Площадь ступенчатой фигуры и будет приближенно равна значению определенного интеграла:
≈ (у 0 + у 1 + … + уn – 1) = 
. (1)
Если взять высоты прямоугольников, равными значениям уi в конечных точках частичных интервалов (рис.2), то
≈ (у 1 + у 2 + … + уn) = 
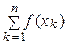. (2)
При выполнении лабораторной работы предлагается взять высоты прямоугольников, равными значениям функции в точках сi =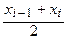 
(серединах отрезков [ xk – 1, xk ]) (рис.3); тогда
≈ (с 1 + с 2 + … + сn) = 
. (3)
Формулы (1)–(3) называются формулами прямоугольников.
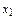
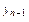
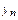
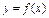Формула трапеций
 |
Заменим кривую f (x) не ступенчатой линией,
как 
в предыдущем случае, а ломаной (рис.4), соединив
соседние точки (xi, yi). Тогда площадь криволиней-
ной трапеции приближенно будет равняться сумме
площадей прямоу 
гольных трапеций, ограниченных
сверху отрезками этой ломаной.
Площадь k -й трапеции равняется Рис.4.
Sk = 
×
(произведение полусуммы оснований на высоту). Здесь уk – 1 и уk – основания трапеции, а xk – xk – 1 = – ее высота. Поэтому
≈ 
= 
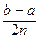
. (4)
Формула (4) называется формулой трапеций.
Формула парабол (Симпсона)
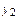Если заменить график функции у = f (x) на
каждом частичном отрезке [ xi – 1, xi ] не прямыми,
а дугами парабол, то получим более точную фор-
|
|
|
мулу приближенного вычисления определенного
интеграла.
Нетрудно показать, что площадь криволи-
нейной трапеции, ограниченной параболой
y = ax 2 + bx + c, проходящей через точки А (0, у 0),
В (
, у 1), С (h, у 2), и прямыми х = 0, х = h, у = 0 Рис.5.
(рис.5), равна
S =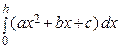 
= 
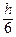(2 ah 2 + 3 bh + 6 c)
или в ординатах точек А, В, С,
S = 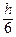(у 0 + 4 у 1 + у 2). (5)
Разобьем отрезок [ a, b ] на 2 n (четное число) равных отрезков точками
a = x 0 < x 1 < x 2 < … < x 2 n -2 < x 2 n -1 < x 2 n = b
и представим интеграл в виде суммы
= 
+ 
+ … + 
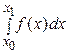. (6)
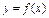
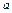
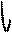
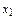
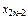
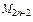
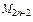
Проведем через точки xk прямые, параллель-
ные оси Оу, и обозначим через
А = М 0, М 1, М 2, …, М 2 n -2, М 2 n -1, М 2 n = В
точки пересечения этих прямых с кривой у = f (x)
(рис.6). Обозначим через у 0, у 1, у 2, …, у 2 n -2, у 2 n -1,
у 2 n ординаты этих точек. Через каждые три точки
М 2 k -2, М 2 k -1, М 2 k (k = 1,2,…, n) проведем параболу с
вертикальной осью симметрии (через три точки, не Рис.6.
лежащие на одной прямой, можно провести единст-
венную параболу). В результате получим n криволинейных трапеций, ограниченных сверху параболами, площадь каждой из которых по формуле (5) равна
= 
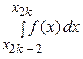(у 2 k -2 + 4 у 2 k -1 + у 2 k).
Подставив в правую часть равенства (4) вместо интегралов их приближенные значения, получим приближенную формулу
= (у 0 + у 2 n + 2(у 2 + у 4 + …+ у 2 n -2) + 4(у 1 + у 3 + …+ у 2 n -1)). (7)
Эта формула называется формулой парабол, или формулой Симпсона.
|
|
|
