Первый и второй законы термодинамики

ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ

 

Изучение студентами биологических специальностей термодинамики и молекулярной физики имеет особое значение, поскольку основные понятия и законы этого раздела общего курса физики активно используются при дальнейшем обучении в курсах физической химии, химии окружающей среды, экологии, биологии и других, а также широко применяются в профессиональной и бытовой деятельности. Поэтому при прослушивании лекций и решении задач на семинарских занятиях следует обращать внимание не только на результаты специальных экспериментов, но и на качественное объяснение соответствующих природных явлений, встречающихся в повседневной жизни.

При изучении курса термодинамики и молекулярной физики можно руководствоваться приведенной ниже рабочей программой, а также использовать дополнительную учебную литературу. Более глубокое понимание законов термодинамики достигается при самостоятельном решении конкретных задач.

Рабочая программа

По курсу термодинамики и молекулярной физики.

 

Предмет, задачи и методы молекулярной физики. Постулаты термодинамики. Первое начало термодинамики. Применение первого начала термодинамики к изопроцессам над идеальным газом.

Адиабатический и политропный процессы. Обратимые процессы, второе начало термодинамики, теоремы Карно, неравенство Клаузиуса, понятие энтропии.

Свободная энергия, энтальпия, потенциал Гиббса, химический потенциал, большой термодинамический потенциал, условие равновесия фаз.

Эргодическая гипотеза, статистика Максвелла-Больцмана, функция распределения Максвелла-Больцмана, барометрическая формула. Распределения Бозе-Эйнштейна и Ферми-Дирака.

Экспериментальные законы переноса, длина свободного пробега, молекулярная теория явления переноса в газах.

Межмолекулярное взаимодействие, уравнение Ван-дер-Ваальса, фазовые переходы, насыщенные пары, свойства жидкостей. Поверхностное натяжение, смачиваемость, капиллярные явления.

Растворы. Закон Рауля. Зависимость растворимости от температуры. Бинарные смеси. Диаграммы состояния бинарных смесей. Осмотическое давление. Химический потенциал. Условия равновесия и устойчивости двухкомпонентной двухфазной системы. Правило Гиббса.

 

Рекомендуемая литература

1. Детлаф А.А., Яворский Б.М., Милковская Л.Б. Курс физики. - М.: Высш. шк., 1973-1979. - Т.1, 2.

2. Зисман Г.А., Тодес О.М. Курс общей физики. - М.: Наука, 1972-1974. -Т.1, 2.

3. Савельев И.В. Курс физики. - М.: Наука, 1989. - Т.1, 2.

4. Волькенштейн В.С. Сборник задач по общему курсу физики. - М.: Наука, 1969.

5. Иродов И.Е. Задачи по общей физике. - М.: Наука, 1988.

6. Мурзов В.И., Коненко А.Ф., Филиппова Л.Г. Общая физика в задачах и решениях. – Мн.: Выш.шк.,1986, 164 с.

 

Указания к решению задач.

Умение решать задачи приобретается систематическими упражнениями. Чтобы научиться решать задачи и подготовиться к выполнению контрольной работы, нужно после изучения соответствующего раздела учебника внимательно разобрать примеры решения типовых задач. Далее следуйте правилам:

ü укажите основные законы и формулы, на которых базируется решение, и дайте словесную формулировку этих законов;

ü разъясните буквенные обозначения формул;

ü дайте чертеж, поясняющий содержание задачи (в тех случаях, когда это возможно); выполнить его надо аккуратно с помощью чертежных принадлежностей;

ü если при решении задач применяется формула, полученная для частного случая, не выражающая какой-нибудь физический закон или не являющаяся определением какой-нибудь физической величины, то ее следует вывести;

ü сопровождайте решение задачи краткими пояснениями;

ü получите решение задачи в общем виде, т.е. выразите искомую величину в буквенных обозначениях величин, заданных в условии задачи, не производя вычислений промежуточных величин;

ü проверьте размерность полученного результата: подставьте в рабочую формулу числовые значения величин, выраженные в единицах одной системы, предпочтительнее в единицах международной системы СИ (исключение из этого правила допускается лишь для тех однородных величин, которые входят в виде сомножителей в числитель и знаменатель формулы с одинаковыми показателями степени);

ü оцените, по возможности, правдоподобность численного ответа.

ЗАКОНЫ ИДЕАЛЬНЫХ ГАЗОВ

Идеальным называется газ, молекулы которого имеют пренебрежимо малый объем и не взаимодействуют до соприкосновения, взаимодействие молекул при соударении происходит по законам абсолютно упругого удара.

 

ОСНОВНЫЕ ФОРМУЛЫ

Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева)

, (1.1)

где p – давление газа, V – его объем, T – абсолютная температура, m – масса газа, M – молярная масса газа, R = 8.31 Дж/(моль∙K) – газовая постоянная.

Замечания. (i) Уравнение состояния (1.1) применяют к газам, взятым при условиях, не слишком отличающихся от нормальных условий (p = 1атм = 1,013∙10⁵ Па, T = 273^oK или t = 0^oC), а также к разреженным газам. Для сильно сжатых (уплотненных) газов, находящихся при очень больших давлениях (свыше 10⁷Па) или при слишком низких температурах уравнение (1.1) неприменимо. (ii) Уравнение состояния (1.1) связывает между собой пять физических величин, характеризующих состояние газа, – p, V, T, m, M – и позволяет по заданным четырем найти пятую величину.

Опытные газовые законы, являющиеся частными случаями уравнения Клапейрона-Менделеева для изопроцессов (процессов, протекающих при неизменном значении какого-либо параметра состояния):

а) закон Бойля-Мариотта (изотермический процесс: T=const и m=const)

pV = const,

б) закон Гей-Люсакка (изобарический процесс: p = const и m=const)

V/T = const,

в) закон Шарля (изохорический процесс: V = const и m=const)

p/T = const.

Молярная масса смеси газов равна

, (1.2)

где ν_i = m_i/M_i - количество молей вещества i -ой компоненты смеси.

Закон Дальтона определяет давление смеси газов

p = ∑ p_i = p₁ + p₂ + p₃ + …+ p_n, (1.3)

где p_i – парциальное давление i -ой компоненты смеси, n – число компонентов смеси.

Концентрация молекул равна 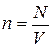, где N – количество молекул в данной системе.

Число частиц в 1 моле вещества равно числу Авогадро

N_A = 6,022 ∙10²³моль^-1.

Постоянная Больцмана

k = 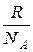= 1,38∙10^-23Дж/K.

 

 

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

 

Пример 1.1 Сколько молекул воздуха находится в комнате, имеющей размеры 8 · 4 · 3 м³, при температуре t = 18^oC и давлении p = 0,97∙10⁵ Па?

Решение. Число частиц N в комнате можно определить, вычислив количество молей воздуха ν в комнате и зная число частиц в одном моле (это – число Авогадро N_A ):

.

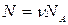Количество молей воздуха в комнате можно определить из уравнения Клапейрона-Менделеева (1.1):

.

Подставляя это выражение в формулу для N, и учитывая, что R/N_A = k – постоянная Больцмана, получаем

.

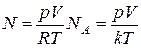Вычисляем значение N, используя данные задачи в единицах системы СИ и температуру в градусах Кельвина

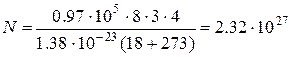
Ответ. В комнате находится 2.32∙10²⁷ частиц воздуха.

Пример 1.2 При температуре t₁ = 20^oC давление воздуха в автомобильной шине p₁ = 6∙10⁵ Па. Найти давление в шине во время движения в автомобиле, если температура воздуха в ней повысится до t₂ = 40^oC. Изменением объема шины пренебречь.

Решение. Так как масса воздуха в шине и объем шины не изменяются, то процесс является изохорическим и из уравнения Клапейрона-Менделеева следует (закон Шарля):

.

Поэтому для нашей задачи имеем

,

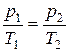откуда находим давление после повышения температуры

.

Подставляем численные значения, учитывая, что в уравнении состояния фигурирует абсолютная температура в градусах Кельвина:

.

Ответ. Давление в шине во время движения автомобиля 6.41∙10⁵ Па.

Пример 1.3 В сосуде объемом V = 30 л содержится идеальный газ при температуре t = 0^оC. После того, как часть газа была выпущена наружу, давление в сосуде понизилось на Δp = 0,78 атм (без изменения температуры). Найти массу выпущенного газа. Плотность данного газа при нормальных условиях ρ₀ = 1,3 г/л.

Решение. Из уравнения состояния (1.1) находим исходную (m₁) и конечную (m₂) массу газа:

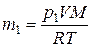и .

Следовательно, масса выпущенного газа равна

.

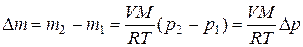В этом выражении осталась неизвестной молярная масса M. Найдем ее из уравнения состояния (1.1) и известной плотности газа при н.у. ρ₀= m₀ / V₀:

.

Подставляя молярную массу в выражение для Δm, получаем

.

Подставляем численные значения, учитывая, что при н.у. давление равно p₀ = 1 атм:

.

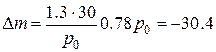Знак минус означает, что масса уменьшилась.

Ответ. Масса выпущенного газа 30,4 г.

Пример 1.4 В трубке, запаянной с одного конца, столбик воздуха заперт столбиком ртути, имеющим длину h = 19 cм. Если трубка расположена вертикально открытым концом вниз, длина столбика воздуха l₁ = 10 cм, а если перевернуть трубку открытым концом вверх, то длина столбика воздуха будет l₂ = 6 cм. Найти атмосферное давление.

Решение. Когда трубка расположена вертикально открытым концом вниз, то давление столбика воздуха p₁ и давление столбика ртути p_r = ρgh (g – ускорение свободного падения, ρ – плотность ртути, h – высота столбика ртути) уравновешиваются атмосферным давлением p_at:

.

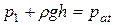Если перевернуть трубку открытым концом вверх, то давление столбика ртути p_r = ρgh и атмосферное давление будут уравновешиваться давлением столбика воздуха p₂

.

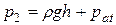Так как масса воздуха в трубке и температура не изменяются, то процесс является изотермическим и подчиняется закону Бойля-Мариотта:

,

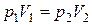где V₁ = l₁S и V₂ = l₂S – объемы воздуха в трубке, расположенной открытым концом вниз и вверх, соответственно, S – площадь поперечного сечения трубки. Подставим выражения для давлений и объемов в этот закон:

,

откуда получаем:

.

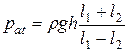Теперь подставим численные значения высоты столбика ртути в системе СИ, из таблиц плотностей возьмем плотность ртути ρ= 3,6∙10³ кг/м³, ускорение свободного падения g = 9,8 м/с²:

.

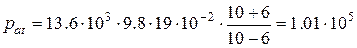Ответ. Атмосферное давление равно 1,01∙10⁵ Па.

Пример 1.5 Сколько ходов n надо сделать, чтобы при помощи поршневого насоса, захватывающего при каждом ходе объем V₀ = 400 см³ воздуха, откачать воздух из стеклянного баллона, имеющего объем V = 1 л, до давления p_n = 10² Па, если первоначальное давление в баллоне p₀ = 10⁵ Па. Температуру воздуха считать постоянной.

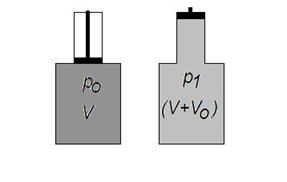
Решение. Проследим за процессом откачки в течение одного хода поршневого насоса. Газ, который вначале занимал объем V при давлении p₀ частично перейдет в камеру насоса, т.е. займет объем (V+V₀). Так как процесс является изотермическим, то выполняется закон Бойля-Мариотта:

,

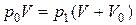отсюда

.

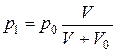Далее воздух из камеры удаляется и поршень приводится в первоначальное положение, при этом масса воздуха уменьшается. Поэтому перед вторым ходом поршня газ в баллоне объема V имеет давление p₁. После второго хода поршня опять получаем

,

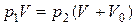отсюда

.

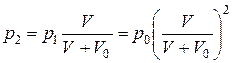Следовательно, после n ходов поршня давление в баллоне будет

.

Чтобы найти n, возьмем логарифм этого выражения и получим:

.

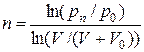Выполнив вычисления, найдем n = 20.

Ответ. Чтобы понизить давление в баллоне до указанной величины, необходимо сделать 20 ходов поршня.

Пример 1.6 Сосуд разделен перегородками на три части, объемы которых V₁, V₂ и V₃, в которых находятся газы при давлениях p₁, p₂ и p₃, соответственно. Какое давление установится в сосуде после удаления перегородок, если температура при этом осталась неизменной.

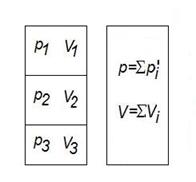Решение. После удаления перегородок каждая газовая компонента в результате диффузии стремится занять весь объем V=V₁+V₂+V₃. Поскольку масса каждой компоненты сохраняется и температура процесса (по условию задачи) неизменна, то для каждой компоненты справедлив закон Бойля-Мариотта:

,

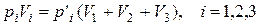где p’_i – парциальное давление i-компоненты в образовавшейся смеси газов. По закону Дальтона находим, что общее давление смеси газов равно сумме парциальных давлений,

.

Пример 1.7 В сосуде емкостью V = 0,5 л находится масса m = 1г парообразного йода. При температуре t = 1000^оC давление в сосуде оказалось равным p = 700 мм рт.ст. Найти степень диссоциации молекул йода J₂ на атомы J при этих условиях. Молярная масса йода J₂ равна M₂ = 254 г/моль.

Решение. В результате диссоциации в сосуде фактически образовалась смесь двух газов J₂ и J. Массу каждой компоненты обозначим m₂ и m₁, соответственно. Очевидно, что общая масса йода при этом сохранилась и равна их сумме m = m₁ + m₂. Тогда степень диссоциации можно определить, как отношение массы образовавшегося атомарного йода к общей массе,

.

Отсюда получим, что

.

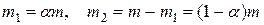Для каждой компоненты из уравнения состояния (1.1) можно определить парциальное давление:

.

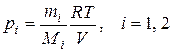Согласно закону Дальтона находим, что общее давление смеси газов, данное в условии задачи, равно сумме парциальных давлений,

.

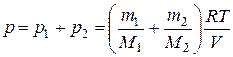Подставим сюда выражения для масс каждой компоненты через α и общую массу m, и учтем, что молярная масса атомарного йода M₁=M₂/2. Разрешая полученное уравнение относительно α, получим

.

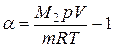Выполним вычисления, переводя значения величин в единицы системы СИ: T=1273^оK, p = 700 мм рт.ст. = 0.7м∙ 13.6∙10³ кг/м³∙9.8 м/с².

Ответ. Степень диссоциации йода α = 0.12.

Пример 1.8 Превышается ли и если да, то во сколько раз значение предельно допустимой концентрации (ПДК) для аммиака, равное 0,2 мг/м³, при обнаружении его запаха, если порог обнаружения запаха для аммиака составляет 46,6 ppm? Атмосферное давление равно 100 кПа, температура 25^оС.

Решение. Для ответа на вопрос необходимо привести объемную концентрацию, соответствующую порогу обнаружения запаха, и ПДК (массовую концентрацию) к одинаковым единицам измерения и найти их отношение. В химии объемная пороговая концентрация в единицах ppm показывает количество объемов данной компоненты V в одном миллионе объемов газовой смеси V₀ при тех же условиях, т.е. в нашем случае

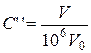= 46,6.

Массовая концентрация определяется как масса вещества компоненты в единице объема газовой смеси, т.е. 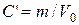. Выразим массу аммиака из уравнения Клапейрона-Менделеева (1.1) и получим массовую концентрацию:

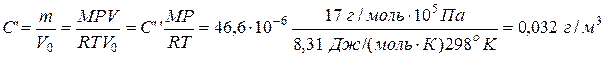
Теперь сравним найденную концентрацию C’ с ПДК:

.

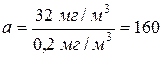Ответ. При обнаружении запаха аммиака, его концентрация в воздухе в 160 раз превышает ПДК.

 

 

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

 

1. Температура воздуха в больничной палате объемом 50 м³ при давлении 740 мм рт.ст. была равна 15^оС. После подогрева воздуха калорифером его температура поднялась до 20^оС. Найти массу воздуха, вытесненного из комнаты.

2. У глубоководных рыб плавательный пузырь выходит через рот наружу, если их извлечь из воды. На основе какого закона можно объяснить это явление?

3. Почему нагретая медицинская банка «присасывается» к телу человека?

4. Гремучая змея реагирует на изменение температуры 0,001^оК. Сможет ли она уловить изменение температуры газа в стеклянном сосуде, если увеличить давление в нем на 1 мм.рт.ст.?

5. Воздух на улицах больших городов может содержать в среднем до 10 мг/м³ окиси углерода за счет выхлопных газов. Определить парциальное давление окиси углерода при температуре 20 ^оС.

6. Объем пузырька воздуха, всплывающего на поверхность со дна озера, увеличился в 2 раза. Определить глубину озера. Температура воздуха на поверхности озера t₂ =27° С, а на дне t₁ =17° С. Атмосферное давление нормальное.

7. Во сколько раз будет превышено значение ПДК для уксусной кислоты, равное 0,2 мг/м³, если на складе произошла авария (разлилась кислота) и установилось динамическое равновесие между парами и жидкой уксусной кислотой? Парциальное давление паров уксусной кислоты принять равным 3 Па. Атмосферное давление равно 101,3 кПа, температура 25^оС.

8. В баллоне объемом V₁ = 200 л при температуре t = 20^оC и давлении p=10⁷Па находится кислород. Найти объем, который газ занимал бы при нормальных условиях.

9. В закрытом баллоне объемом V = 2л находится воздух, давление которого p₁ = 0.53∙10⁵ Па при комнатной температуре. Затем баллон опускается в воду той же температуры и на глубине h = 1,2 м открывается. Какой объем воды войдет в баллон, если атмосферное давление равно p₀ = 0,99∙10⁵ Па?

10. В сосуде находится смесь m₁ = 7г азота и m₂ = 11г углекислого газа при температуре t = 17^оC и давлении p = 1 атм. Найти плотность этой смеси, считая газы идеальными.

ПЕРВЫЙ И ВТОРОЙ ЗАКОНЫ ТЕРМОДИНАМИКИ

В основе термодинамики лежат экспериментально установленные законы, которые называют первым и вторым началами термодинамики. С помощью этих законов можно, не делая предположений о молекулярном строении изучаемых тел, получить многие сведения об их свойствах в различных условиях. В то же время молекулярная физика дает возможность связать макроскопические параметры системы с микроскопическими характеристиками вещества.

 

ОСНОВНЫЕ ФОРМУЛЫ

 

Первое начало термодинамики: количество теплоты Q, сообщенное системе, идет на увеличение ее внутренней энергии U и совершение системой работы A над окружающими телами:

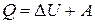. (2.1)

Внутренняя энергия идеального газа равна

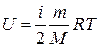, (2.2)

где i – число степеней свободы частицы газа, которое равно числу независимых координат, определяющих положение и ориентацию молекулы.

 

Для одноатомной молекулы газа:	i=3 (поступательные степени свободы).
Для жесткой двухатомной молекулы:	i=5 (3 поступательные и 2 вращательные).
Для жесткой трехатомной молекулы:	i=6 (3 поступательные и 3 вращательные).

 

Удельная теплоемкость – это скалярная величина, численно равная количеству теплоты, необходимому для нагревания 1 кг вещества на 1^оК,

. (2.3)

Удельная теплота плавления λ, удельная теплота парообразования r, удельная теплота сгорания q – это скалярные величины, численно равные количеству теплоты, необходимому для плавления, парообразования, сгорания, соответственно, 1 кг вещества при соответствующей температуре,

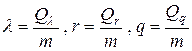. (2.4)

Удельные теплоемкости газа при постоянном объеме c_V и при постоянном давлении c_p равны

и 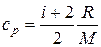. (2.5)

Удельная теплоемкость газа, состоящего из n компонент:

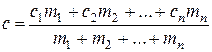. (2.5.1)

Адиабатическим процессом называется термодинамический процесс, осуществляемый без теплообмена с окружающими телами. Уравнение адиабаты (Пуассона) идеального газа

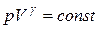, (2.6)

где показатель адиабаты определяется отношением удельных (или молярных) теплоемкостей:

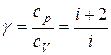. (2.6.1) При элементарном расширении газа совершается работа:

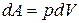, (2.7)

работа при изобарическом процессе:

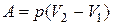, (2.7.1)

работа при изотермическом процессе:

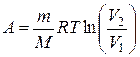, (2.7.2)

работа при адиабатическом процессе:

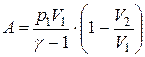. (2.7.3)

Энтропия есть функция состояния системы, дифференциал которой при элементарном обратимом процессе равен отношению бесконечно малого количества теплоты, сообщенного системе, к абсолютной температуре последней. При переходе системы из состояния А в состояние В изменение энтропии равно

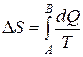. (2.8)

Энтропия сложной системы равна сумме энтропий ее однородных частей.

Статистическое определение энтропии (формула Больцмана)

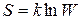, (2.9)

где k – постоянная Больцмана, W – термодинамическая вероятность, т.е. число способов, которыми можно осуществить данное макроскопическое состояние системы.

Второе начало термодинамики: энтропия замкнутой системы не уменьшается – она возрастает при необратимых процессах или остается постоянной в случае обратимых процессов,

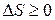. (2.10)

Изменение энтропии 1 моля идеального газа при переходе из состояния 1 в состояние 2:

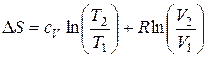. (2.11)

Замечание. В термодинамическом отношении многие системы (включая биологические) являются открытыми, поскольку через свои границы обмениваются веществом и энергией с окружающей средой. Они могут проходить через ряд неравновесных состояний, при которых возможно уменьшение энтропии. Такие процессы называются самоорганизацией системы. Уменьшение энтропии в процессе роста живых систем происходит за счет свободной энергии, освобождаемой при распаде поглощаемых извне питательных веществ или за счет энергии солнца (фотосинтез).

 

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Пример 2.1 Чему равны удельные теплоемкости c_p и c_V некоторого двухатомного газа, если плотность этого газа при нормальных условиях равна ρ₀ = 1.43 кг/м³ ?

Решение. Удельные теплоемкости газа при постоянном объеме и постоянном давлении, согласно формулам (2.4), равны

и .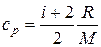

В этих выражениях нужно определить величины i и M. Для двухатомного газа число степеней свободы i = 5, молярную массу M найдем из уравнения Клапейрона-Менделеева (1.1) и данной в условии плотности газа, ρ₀ = m / V:

.

Подставляя это выражение в формулы для теплоемкостей, получаем

Вычисления проводим, учитывая, что при н.у. p₀ = 1.013∙10⁵ Па, T₀ = 273^оK.

Ответ. c_p = 650 Дж/(кг∙K), c_V = 908 Дж/(кг∙K)

Пример 2.2 Азот занимает объем V = 2 л под давлением p = 10⁵ Па. Какое количество теплоты надо сообщить азоту, чтобы

а) при p = const объем увеличить вдвое?

б) при V = const давление увеличить вдвое?

Решение. Согласно первому началу термодинамики (2.1), необходимое количество теплоты

.

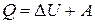Найдем изменение внутренней энергии и совершенную работу в обоих случаях.

а) p = const. Согласно формуле (2.2) изменение внутренней энергии

.

Из уравнения состояния (1.1) и условия V₂ = 2V₁ = 2V находим, что

.

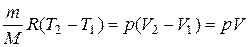Поэтому получаем

.

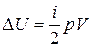Cовершенная работа при условии V₂ = 2V₁ = 2V равна

.

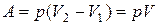Окончательно,

.

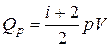б) V = const. Согласно формуле (2.2) изменение внутренней энергии

.

Из уравнения состояния (1.1) и условия p₂ = 2p₁ = 2p находим, что

.

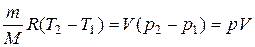Поэтому также как в предыдущем случае получаем

.

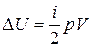Но в отличие от предыдущего случая, совершенная работа при постоянном объеме A=0. Следовательно, необходимое количество теплоты равно

.

Вычисления проводим, учитывая, что азот – двухатомный газ с числом степеней свободы i = 5 и его объем в единицах СИ равен 1 л = 10^-3 м³.

Ответ. Q_p = 700 Дж, Q_V = 500 Дж.

Пример 2.3 Масса m = 10,5 г азота изотермически расширяется при температуре t = -23^oC от давления p₁ = 2,5 атм до p₂ = 1 атм. Найти работу, совершенную газом при расширении.

Решение. По определению (2.7), работа, совершенная газом при расширении, равна

.

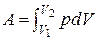В общем случае давление зависит от изменения объема. Эту зависимость можно найти из уравнения состояния (1.1), а именно,

,

причем для изотермического процесса T = const, поэтому имеем

.

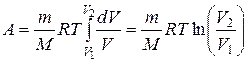В этом выражении нам неизвестно отношение V₂/V₁, которое можно найти с помощью закона Бойля-Мариотта V₂/V₁ = p₁/p₂ , следовательно

.

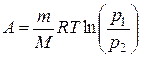Подставим численные значения, учитывая, что абсолютная температура процесса T = -23+273 = 250^оK, и молярная масса азота M= 28 г/моль.

Ответ. A = 720 Дж.

Пример 2.4 Газ расширяется адиабатически, при этом его объем увеличивается вдвое, а абсолютная температура падает в 1,32 раза. Какое число степеней свободы имеют молекулы данного газа?

Решение. Так как масса газа не изменяется, то согласно уравнению адиабаты (2.6) для газа в начале и в конце процесса, имеем:

.

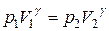Чтобы выразить неизвестные давления через температуры газа в начале и в конце процесса, воспользуемся уравнением состояния (1.1) в виде:

.

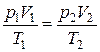Отсюда следует, что

.

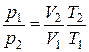С учетом предыдущего, получаем: . Возьмем логарифм левой и правой частей этого равенства, отсюда находим

.

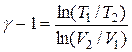Принимая во внимание связь показателя адиабаты с числом степеней свободы молекул газа (2.6.1), γ= c_p/c_V = (i + 2)/i, окончательно получаем

.

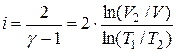Осталось провести вычисления, используя условия задачи:

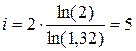
Ответ. Число степеней свободы данного газа i = 5, следовательно, газ двухатомный.

Пример 2.5 Двухатомный газ, находящийся при температуре t₁=27^оC и давлении p₁ = 2∙10⁶ Па сжимается адиабатически от объема V₁ до объема V₂ = 0,5V₁. Найти температуру t₂ и давление p₂ газа после сжатия.

Решение. Поскольку газ двухатомный, то число степеней свободы его частицы i = 5, а показатель адиабаты γ=(i+2)/i = 7/5 = 1,4. Тогда давление после сжатия можно сразу же найти из уравнения адиабаты (2.6):

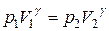, отсюда .

Чтобы найти температуру после сжатия, воспользуемся уравнением состояния (1.1)

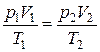, отсюда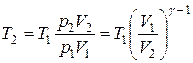

Подставляем численные значения, учитывая, что T₁ = 27 + 273 = 300^оK.

Ответ. t₂ = 123^оC; p₂ = 52,8∙10⁵ Па.

Пример 2.6 Найти изменение энтропии при превращении m = 10 г льда при t₁ = -20^oC в пар при t₂ = 100^oC. Удельная теплоемкость льда c_i=2,1∙10³ Дж/(кг∙К), удельная теплоемкость воды c_h=4,2∙10³ Дж/(кг∙К), удельная теплота плавления λ=3,35∙10⁵ Дж/кг, удельная теплота парообразования r=2,26∙10⁶ Дж/кг.

Решение. По определению (2.8), изменение энтропии равно

.

Рассматриваемый сложный процесс состоит из четырех этапов: (1) нагревание льда, (2) плавление льда, (3) нагревание воды, (4) парообразование. На каждом этапе переданное количество теплоты идет на увеличение внутренней энергии или на преобразование структуры вещества.

Изменение энтропии на этапе нагревания льда до температуры плавления t₂= 0^oC (T₂ = 273^oK), с учетом (2.3), составит

,

в процессе плавления льда, с учетом определения (2.4):

,

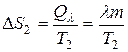на этапе нагревания воды до температуры кипения T₃ = 373^oK:

,

в процессе кипения воды:

.

Полное изменение энтропии равно сумме

.

После подстановки значений получаем ответ.

Ответ. Изменение энтропии равно ΔS = 88 Дж/К.

Пример 2.7 Азот массой m = 10,5 г изотермически расширяется от объема V₁= 2 л до объема V₂= 5 л. Найти изменение энтропии в этом процессе.

Решение. По определению, изменение энтропии равно

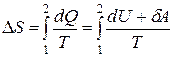
Так как в изотермическом процессе температура не изменяется, то dU= 0, поэтому dQ=δA=pdV. Из уравнения состояния (1.1) выразим давление , подставим в формулу для изменения энтропии и проинтегрируем:

.

После подстановки значений, учитывая, что молярная масса азота M=28 г/моль, получаем ответ.

Ответ. Изменение энтропии равно ΔS = 2,85 Дж/К.

Пример 2.8 При нагревании ν = 1 кмоль двухатомного газа его абсолютная температура увеличивается в 1,5 раза. Найти изменение энтропии при: 1) изохорном нагревании и 2) при изобарном нагревании газа.

Решение. По определению, изменение энтропии равно

.

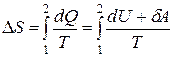При изохорном нагревании работа не совершается, δA = pdV = 0. Изменение внутренней энергии dU = (m/M)(i/2)RdT, поэтому

.

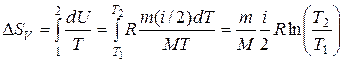При изобарном процессе совершается работа δA = pdV = (m/M)RTdV/V. Изменение внутренней энергии dU = (m/M)(i/2)RdT, поэтому

.

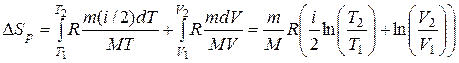В этом выражении нам неизвестно отношение объемов V₂/V₁ . Его можно найти по закону Гей-Люссака: V₂/V₁ = T₂/T₁. Отсюда получаем

.

Подставляем численные значения, учитывая, что в условии задачи дано число молей ν=m/M, T₂/T₁ = 1,5 и число степеней свободы двухатомного газа i = 5.

Ответ. ΔS_V = 8,42∙10³ Дж/К, ΔS_p = 11,8∙10³Дж/К

Пример 2.8 Кислород массой 1 кг занимает объем V₁. Определить вероятность самопроизвольного изотермического сжатия кислорода на 10^-6 часть первоначального объема.

Решение. Пусть W₁ – вероятность того, что кислород занимает объем V₁, W₂ – вероятность того, что после самопроизвольного изотермического сжатия его объем V₂. Изменение энтропии согласно формуле Больцмана (2.9) равно

.

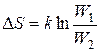С другой стороны, при изотермическом изменении объема

.

Приравнивая правые части этих выражений, получим

.

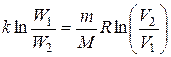Следовательно,

.

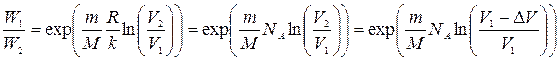Подставим заданные числовые значения и учтем, что 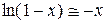при малых х=ΔV/V₁. Получим .

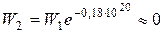Ответ. Вероятность самопроизвольного изотермического сжатия газа практически равна нулю.

 

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

11. Найти удельные теплоемкости c_p и c_V некоторого двухатомного газа, если известно, что его молярная масса равна M=30 г/моль³ и отношение c_p/c_V=1,4.

12. Азот находится в закрытом сосуде объемом V = 3 л при температуре t = 27^oC и давлении p = 3 атм. После нагревания давление в сосуде повысилось до p = 25 атм. Определить температуру азота после нагревания и количество теплоты, переданное газу.

13. Для нагревания некоторого количества газа на Δt = 50^оC при постоянном давлении необходимо затратить Q₁ = 672 Дж теплоты. Если это же количество газа охладить на Δt = 100^оC при постоянном объеме, то выделится Q₂