 |
5. Закон обратного отношения между объемом и содержанием понятия.
|
|
|
|
Обобщение и ограничение понятий.
Содержанием понятия называется совокупность существенных признаков одноэлементного класса или класса однородных предметов, отраженных в этом понятии. Содержанием понятия “квадрат” является совокупность двух существенных признаков: “быть прямоугольником” и “иметь равные стороны”.
Объемом понятия называют совокупность (класс) предметов, которая мыслится в понятии.
Закон обратного отношения между объемами и содержаниями понятий
В этом законе речь идет о понятиях, находящихся в родовидовых отношениях. Объем одного понятия может входить в объем другого понятия и составлять при этом лишь его часть. Например, объем понятия “хищная рыба” целиком входит в объем другого, более широкого по объему понятия “рыба” (составляет часть объема понятия “рыба”). При этом содержание первого понятия оказывается шире, богаче (содержит больше признаков), чем содержание второго. На основе обобщения такого рода примеров можно сформулировать следующий закон: чем шире объем понятия, тем уже его содержание, и наоборот. Этот закон называется законом обратного отношения между объемами и содержаниями понятий. Он указывает на то, что чем меньше информации о предметах, заключенной в понятии, тем шире класс предметов и неопределеннее его состав (например, “водопад”), и наоборот, чем больше информации в понятии (например, “крупный водопад” или “крупный водопад в Канаде”), тем уже и определеннее круг его предметов, или даже мыслится только один предмет.
Обобщение понятия – это совершение перехода от понятия с меньшим объемом, но большим содержанием к понятию с большим объемом и меньшим содержанием. При обобщении осуществляется переход от видового понятия к родовому.
|
|
|
Например, обобщая понятие «хвойный лес», мы переходим к понятию «лес». Содержание этого нового понятия уже, зато объем значительно шире. Содержание уменьшилось, потому что мы изъяли (убрав слово «хвойный») ряд характерных видовых признаков, отражающих особенности хвойного леса.
Ограничение понятия – это логическая операция, противоположная обобщению. Если обобщение идет по пути постепенного отстранения от признаков предмета, ограничение, напротив, обогащает совокупность признаков понятия. Таким образом, осуществляется переход от общего к частному, от вида к роду, от единичных понятий к общим.
Эта логическая операция характеризуется уменьшением объема за счет расширения содержания.
Операция ограничения не может продолжаться дальше, когда в его процессе достигается единичное понятие. Оно характеризуется максимально полным содержанием и объемом, в котором мыслится лишь один объект.
6. Деление как логическая операция. Правила деления и ошибки в делении.
Деление понятий – это операция, с помощью которой объем понятия разбивается на подвиды, представляющие собой совокупности предметов, мыслимых в этом понятии. Процесс деления может быть охарактеризован также как процесс выявления возможных видовых понятий.
6.
В составе каждого деления выделяют: делимое понятие, т. е. понятие, которое делят; основание деления, т. е. признак, по которому происходит деление; члены деления – видовые понятия по отношению к исходному.
Принято различать правильное и неправильное деление.
Деление является правильным, если оно удовлетворяет следующим пяти условиям или правилам деления.
1. Деление должно происходить по одному определенному основанию. При этом основание деления может представлять собой сочетание двух или даже более различных признаков. Например, можно произвести операцию деления понятия «механическое движение» по основанию, состоящему из двух признаков: характеру траектории и состоянию скорости во времени, получив в результате такие понятия: «прямолинейное и равномерное движение», «прямолинейное и равноускоренное движение», «прямолинейное и равнозамедленное движение», «криволинейное и равномерное движение» и т. д. Несоблюдение этого правила приводит к логической ошибке – «смешению оснований». Смешение оснований происходит, например, когда понятие «преступление» делится на «умышленные», «неумышленные» и «должностные». Члены деления не должны пересекаться, исключать друг друга.
|
|
|
2. Полученные при делении понятия должны быть попарно несовместимы. Примером логической ошибки на это правило является операция деления понятия «параллелограмм» на «прямоугольники», «ромбы» и «квадраты», поскольку такие пары понятий, как «квадрат» и «ромб», «квадрат» и «прямоугольник», не взаимоисключающие. Будет ошибкой деление с излишним членом, когда в результате деления указанное понятие не является видом данного рода.
3. Деление должно быть соразмерным, сумма объёмов членов деления должна быть равна объёму делимого понятия. Члены деления должны исчерпывать объем делимого понятия, т. е. объединение их должно быть равно этому объему. Нарушение этого правила приводит к двоякого рода ошибке. Во-первых, «неполное деление», которое имеет место, когда в результате деления указаны не все виды делимого родового понятия. Например, в случае деления понятия «часть речи» на «имя существительное», «имя прилагательное» и «глагол». Во-вторых, «деление с излишним членом», которое имеет место в том случае, когда кроме видов делимого понятия указывают члены деления, не являющиеся видами данного рода. Например, «химические элементы» делятся на «металлы», «неметаллы», «сплавы» (сплавы не являются химическими элементами).
4. Никакой из членов деления не должен быть пустым классом.
5. Деление должно быть непрерывным, т. е. все его члены являются ближайшими видами объема исходного понятия, выделяемыми по выбранному основанию. Логическая ошибка, возникающая при несоблюдении этого правила – «скачок в делении». Например, в операции деления будет допущена ошибка, если понятие «сказуемое» разделить на «простое», «составное глагольное» и «составное именное». Правильным будет сначала разделить понятие «сказуемое» на «простое» и «составное», а затем «составное» разделить на «составное глагольное» и «составное именное». Члены деления должны быть видами одного порядка.
|
|
|
В логике принято различать два вида деления:
─ видовое деление;
─ дихотомическое.
Видовое деление – деление по видоизменяющимся признакам, производится таким образом, что член деления содержит родовой признак, но в новом качестве.
Так, например, понятие «студент» можно разделить на следующие: «студент дневной формы обучения», «студент вечерней формы обучения», «студент заочной формы обучения». Основанием деления в данном случае служит форма обучения.
Дихотомическое деление – путём деления родового понятия на два взаимоисключающих друг друга видовых понятия. В процессе дихотомического деления делимое понятие делится на два противоречащих понятия. Например, понятие «преступление» делится на «преднамеренное преступление» и «непреднамеренное преступление».
Операцию деления понятия нельзя смешивать с расчленением предмета на части.
Цель деления понятия – установить те предметы, которые присущи содержанию родового понятия.
Цель операции членения понятия – установить структуру и состав предмета.
Отличить эти две операции можно следующим образом. В случае операции деления содержание делимого понятия всегда можно утверждать относительно каждого члена деления, получая при этом истинные высказывания. В случаях же членения предмета на части получаются бессмысленные высказывания.
7. Типы отношений между понятиями.
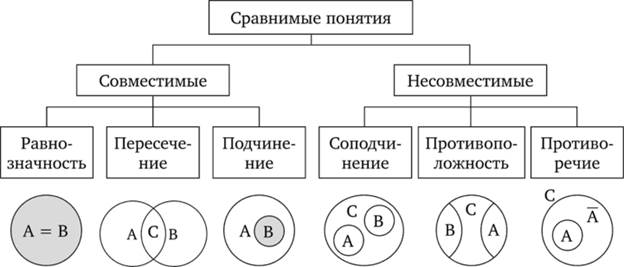
По содержанию могут быть два вида отношений между понятиями – сравнимость и несравнимость.
1). Сравнимыми называются понятия, отражающие некоторые общие существенные признаки предмета или класса однородных предметов. Например, «право», «политика», «мораль» (общественное явление), «юрист» и «адвокат» (высшее юридическое образование), «взятка» и «кража» (правонарушения). Степень сравнимости понятий может быть различной, а сами сравнения – весьма разнообразными, отражающими всё многообразие отношений предметов и явлений в окружающем мире.
|
|
|
2). Несравнимые понятия не имеют общих признаков, далеки друг от друга по своему содержанию. Например, «симфоническая музыка» и «кассационная жалоба», «процессуальные акты предварительного расследования» и «общая тетрадь», «государство» и «всемирное тяготение».
В логических отношениях могут находиться только сравнимые понятия. Логический анализ несравнимых понятий невозможен.
В зависимости от того, как соотносятся объёмы сравнимых понятий, понятия делятся на две группы: совместимые и несовместимые.
|
|
|


