Геометрический и энергетический смысл уравнения Бернулли

Виды движения жидкости

Установившееся и не установившееся.

Установившееся – неизменное по времени, при котором гидромеханическое давление и скорость, являются функциями лишь координат, но не зависимости от времени.

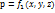и

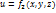
Установившееся – приток равен расходу.

Неустановившееся – давление и скорость зависят как от координат, так и от времени.

Постепенное опустошение тары.

Элементарный объем жидкости совершает 3 вида движения: поступательное, вращательное и деформационное.

По желанию…. поступательное движение; благодаря этому движению центр О пучка радиусов перемещается в точку О1', выделяя это движение, надо в точке О' представить себе начальную окружность, радиусы которой параллельны соответствующим радиусам окружности с ценром в точке О; б) вращательное движение; благодаря этому движению главные оси деформации / —/ и II—II круглого элементарного объема жидкости, представленного в точке О', поворачиваются на некоторый угол dQ; при этом поясненные выше отрезки ab должны сохранять свою длину (как в случае твердого тела); в) деформационное движение; благодаря этому движению каждый из намеченных радиусов поворачивается еще на дополнительный угол dQ' и, кроме того, удлиняется или укорачивается;1 углы dQ' поворота (дополнительные к среднему углу dQ

 

Виды насадок

Различают 5 типов насадок:

1)Внешний цилиндрический насадок (Насадок Вентури)

2)Внутренний цилиндрический насадок (насадок Борда)

3)Конический сходящийся насадок

4)Конический расходящийся насадок

5)Коноидальный насадок

45. Уравнение удельной энергии Удельной энергией потока Е называется энергия массы жидкости, протекающей в единицу времени через живое сечение потока, отнесенная к единице веса и определяемая относительно плоскости сравнения. Удельная энергия потока, определяемая относительно плоскости сравнения, хорошо описывается уравнением Д.Бернулли . В этом выражении исключим атмосферное давление, являющееся постоянным по всей свободной поверхности потока, и вместо него введем манометрическое давление. Для любой точки М живого сечения гидродинамическое давление будет равно 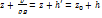, где h – наибольшая глубина в живом сечении. Тогда удельная энергия выразится уравнением: 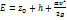. Если плоскость сравнения провести через низшую точку живого сечения, то Z0 будет равно нулю, и удельную энергию в данном живом сечении относительно этой плоскости сравнения называют удельной энергией сечения Э: 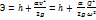. Движение жидкости происходит за счет энергии потока Е, поэтому последняя по пути потока должна уменьшаться, т.е.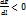

Вискозиметр Энглера

Для измерения вязкости служат приборы, называемые вискозиметрами.

Для определения вязкости капельных жидкостей широкое распрост­ранение получил вискозиметр Энглера, который представляет собой ме­таллический цилиндрический сосуд объемом 200 см3, наполняемый сна­чала дистиллированной водой при температуре 20°С, а затем испытуе­мой жидкостью. Жидкость вытекает из сосуда через круглое отверстие диаметром около 3 мм.

За вязкость по Энглеру принимается отношение времени t истечения 200 см3 испытуемой жидкости ко времени tB истечения того же объема дистиллированной воды при температуре 20°С, равному 51,6 с. Таким образом, вязкость по Энглеру (условная вязкость в градусах Энглера), обозначаемая обычно °Е, определяется зависимостью

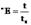
Для перехода от вязкости в градусах Энглера к коэффициенту кинематической вязкости n применяется формула Убеллоде:

.

 

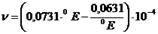Градус Энглера, градус ВУ — внесистемная единица условной вязкости (ВУ) жидкостей, применяемая в технике, особенно в нефтяной и химической промышленности и названная по имени немецкого химика К. О. Энглера.

Число градусов Энглера определяется отношением времени истечения (в сек) 200 см³ испытуемой жидкости при данной температуре из вискозиметра типа ВУ (Энглера) ко времени истечения (в сек) 200 см³ дистиллированной воды из того же прибора при нормальной температуре (20 °C).

Перевод градусов Энглера в единицы кинематической вязкости производится по эмпирической формуле или таблице.

Вихревое движение

Вихревое движение – движение вызванное вращением элементарного объема. Угловая скорость вращения элементарного объема жид-ти наз-ся вихрем, а линия касательная во всех точках к векторам вихря- вихревой линией.Поверхность образованная вихревыми линиями проведенные через все точки элементарного замкнутого контура наз-ся вихревой трубкой, а жид-ть заключенную внутри вихревой трубки- вихревой нитью.

Геометрический и энергетический смысл уравнения Бернулли

Предположим, что центры тяжести живых сечений струйки 1-1 и 2-2 (рис 1) расположены на высотах z₁ и z₂ от плоскости сравнения 0-0 и что в этих центрах тяжести расположены пьезометрические трубки. Жидкость в каждой трубке поднимется на высоту h_i =p_i/сg, т.е. на пьезометрическую высоту. В уравнении (8) z₁ и z₂ (м) представляют собой геометрические высоты центров тяжести соответствующих живых сечений струйки над плоскостью сравнения, члены p₁/сg и p₂/сg (м) - пьезометрические высоты, отвечающие давлениям в указанных центрах тяжести. Третий член уравнения u_i²/2g (м) является скоростным или динамическим напором, соответствующий скорости u_i.

Отложим от точки А отрезок Аа, равный пьезометрической высоте p₁/сg, а от точки В - отрезок Вb, равный p₂/сg. Затем от точек a и b отложим отрезки аа^/ и bb^/, соответствующие скоростным напорам u₁²/2g и u₂²/2g.

Аналогичные построения можно сделать для ряда живых сечений, взятых вдоль элементарной струйки. Т.к. сумма трех членов u_i²/2g, p_i/сg и z_i для идеальной жидкости постоянна вдоль оси струйки, то вершины вертикальных отрезков аа^/ и bb^/располагаются на одинаковых вертикальных расстояниях от плоскости сравнения 0-0, и вершины этих отрезков должны лежать в одной горизонтальной плоскости, называемой напорной плоскостью 0^/-0^/. В случае идеальной жидкости напорная плоскость является горизонтальной. Если плавно соединить уровни жидкости в пьезометрических трубках, то получим пьезометрическую линию p-p.

Сумма трех высот называется полным гидродинамическим напором и обозначается H_Д. Следовательно, полный напор представляет собой сумму потенциального H = z + p/сg и скоростного h_ck= u²/2g напоров, т.е.

H_Д=H+h_ск.

Гидростатический парадокс

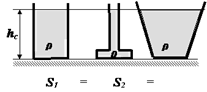Рассмотрим три сосуда разной формы, заполненные жидкостью до одного уровня hc. Все сосуды такие, что имеют одинаковую площадь дна.

В соответствии с общей формулой определения силы, действующей на плоскую поверхность

,

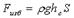можно вычислить силу, действующую на дно сосуда. Для всех трёх сосудов эти силы окажутся одинаковыми и независящими от веса жидкости в сосуде. Но на опору все сосуды будут действовать с разными силами, равными весу сосудов с жидкостью. Этот факт получил название гидростатического парадокса.

Различные по форме сосуды, имеющие одинаковые площадки доньев и заполненных на одинаковой жидкостью на одну и ту же высоту, будут иметь одинаковую силу давления на дно независимо от формы сосуда и количества в ней жидкости.

Гидравлический удар

Гидравлический удар — явление резкого изменения давления в напорном трубопроводе при внезапном изменении скорости движения жидкости, связанном с быстрым закрытием или открытием задвижки, крана, клапана и т. п., быстрым остановом или пуском гидродвигателя или насоса. В указанных случаях при уменьшении или увеличении скорости движения жидкости давление перед запорным устройством соответственно резко увеличивается (положительный гидравлический удар) или уменьшается (отрицательный гидравлический удар). Это изменение давления распространяется по всей длине трубопровода L (рис.) с большой скоростью а, называемой скоростью распространения ударной волны.

Гидравлический удар может быть полным, когда происходит полный останов движения, или неполным, когда начальная скорость движения жидкости υ₀изменяется до некоторого значения υ, что имеет место, например, при частичном перекрытии запорного устройства. Гидравлический удар может быть также прямым, когда закрытие задвижки, крана происходит достаточно быстро, а именно, при t _закр < t _фаз, или непрямым, когда торможение жидкости происходит при менее быстром перекрытии запорного устройства

Величина а определяется теоретической формулой Н. Е. Жуковского: 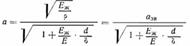где Е_ж — объемный модуль упругости жидкости плотностью ρ; численные значения Е_ж и ρ; приведены в разделе "Лекции по гидравлике"; Е — модуль упругости материала трубы; d — диаметр трубы; δ —толщина стенок трубы; а_зв — скорость распространения звука в данной упругой среде; для воды эта скорость равна 1435 м/с, для бензина — 1116 м/с, для масел — 1200—1400 м/с.

Повышение (заброс) давления при прямом гидравлическом ударе определяется по формулам Н. Е. Жуковского:
при полном ударе Δp= ρ ·a·υ₀

при неполном ударе

Δp= ρ ·a·(υ₀-υ)

Повышение давления при непрямом гидравлическом ударе определяется по приближенным формулам:
при полном ударе

Δp= ρ ·2·L·υ₀/ t _закр

при неполном ударе

Δp= ρ ·2·L·(υ₀-υ)/ t _закр

Наиболее опасным является положительный полный прямой гидравлический удар, при котором повышение давления может достигать значительной величины.

Гидравлический удар может вызвать разрыв трубопроводов, разрушение деталей гидромашин и приборов, несвоевременную сработку отдельных устройств гидросистем (реле давлений, реле времени, гидрозамков и др.).
Интенсивность гидравлического удара снижается путем увеличения длительности сработки запорных устройств; локализуется он установкой на трубопроводе вблизи места возможного возникновения гидравлического удара уравнительных башен, воздушных колпаков, предохранительных клапанов и др.

Давление в точке покоящейся жидкости.

Гидростатика – раздел гидравлики, в которой изучаются законы равновесия жидкостей, а так же тв. Тел, полностью или частично погруженных в жидкость.

Гидростатическое давление – величина, характеризующая напряженно-деформированное состояние частицы жидкости. Давление в точке покоящейся жидкости обладает двумя св-вами.

Первое св-во. Давление в точке покоящейся жидкости всегда нормально к поверхности (площадке), воспринимающей это давление. Это св-во не требует доказательства, т.к. оно очевидно.

Второе св-во. Давление в точке покоящейся жидкости во всех направлениях одинаково по величине, т.е. яв-ся скаляром.

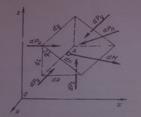Для доказательства этого сва-ва возьмем внутри жидкости, находящейся в равновесии, точку А и выделим вокруг нее бесконечно малый объем жидкости dV в виде треугольной призмы с ребрами dx,dy,dl,dn, причем угол наклона ребра dn к ребру dz взят произвольным. Отбросим мысленно к каждой грани соотв. Элементарные силы гидростатического давления dP_x=P_xdldz,dP_z=P_zdldx,dP_n=P_ndldn и т.д.,которые, как было указано выше, действуют нормально граням и будут направлены внутрь рассматриваемого объема.

 

Кроме этих поверхностных сил на жидкость, находящуюся внутри призмы, действуют еще массовые силы, результирующая которых приложена в центре тяжести объема и в общем случае равна:

dM-dmF= dVF= 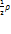Fdxdzdl

123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: