 |
Минимальные квалификационные требования и нритические показатели
|
|
|
|
Практические потребности и подводные камни. Понятие овладения (mastery) в предметно-ориентированном тестировании — это только один пример использования критических показателей в принятии решения. Повседневная жизнь обязывает точно формулировать и выполнять минимальные квалификационные требования к человеческой деятельности в самых различных областях. Во многих ситуациях соображения безопасности требуют установления критических, граничных точек в исполнении деятельности, как при выдаче водительских прав, отборе летчиков гражданской авиации или найме рабочих для обслуживания ядерных установок. В области образования прохождение университетского курса или окончание школы представляют собой другие ситуации, которые также требуют классификации людей по принципу «все или ничего» (Jaeger, 1989). В клинической и консультационной практике решения, касающиеся выбора лечения или линии поведения, могут требовать аналогичных, дихотомических, оценок.
Особо сильный довод в пользу применения граничных показателей связан с наличием критических переменных, необходимых для выполнения некоторых функций. Критическими называют такие переменные, недостаток в которых не может быть компенсирован выдающимися способностями или высочайшей квалификацией в областях, связанных с другими параметрами деятельности. В таких случаях высокий показатель по комплексной батарее профотбора мог бы маскировать недостаток критического умения. Однако при использовании граничных значений все те, кто не набрал требуемого минимума баллов по критическому умению, считаются не прошедшими
Глава 3. Нормы и смысловое значение тестовых показателей
|
|
|
99
отбор, независимо от их других способностей и умений. Например, гидроакустики должны обладать высокой слуховой различительной чувствительностью. Во время Второй мировой войны новобранцев ВМФ США первоначально отбирали для обучения специальности гидроакустика на основе их совокупных показателей по тестам слухового различения и понимания механических закономерностей. В результате, целый ряд мужчин, обучавшихся до войны в колледже и потому сведущих в механике, но, к сожалению, не обладавших требуемым уровнем развития слухового различения, был зачислен на курсы гидроакустиков, с последующим отсевом. В соответствии с заведенным в ВМФ порядком несправившихся с первым учебным заданием переводили на неквалифицированную работу — учениками матросов, теряя в связи с этим возможность использовать их в качестве специалистов. Дополнительный анализ сложившегося положения привел со временем к замене критерия отсева в процедуре отбора по этой военной специальности. Однако для большинства имеющих отношение к работе переменных их связь с эффективностью труда носит линейный характер, так что чем выше показатель по тесту, тем лучше, в общем, человек справляется с работой (Coward, & Sackett, 1990). В таких случаях, фактический показатель человека по соответствующему тесту является лучшим прогнозирующим параметром, чем его положение относительно граничной точки.
Коль скоро невозможно избежать использования критических показателей при принятии многих практических решений, важно сознавать подводные камни таких оценок и применять меры для сокращения ошибочных решений. Например, нужно стремиться смягчать ограничивающее действие единственного тестового показателя. Когда это возможно, следует предпочесть критический интервал или группу критических показателей одному-единственному показателю, полученному при однократном проведении конкретного теста. Кроме того, решения, принимаемые в отношении конкретных лиц, должны основываться на информации из разных источников, дополняющих тестовые показатели другими релевантными данными в отношении интересующей деятельности в прошлом и настоящем. Если граничные значения показателей по тестам устанавливаются группой экспертов, в ней должно быть обеспечено адекватное представительство специалистов как в области предполагаемой профессиональной деятельности, так и в области конструирования и применения тестов. Самое главное, при появлении возможности граничные значения показателей следует определять или верифицировать на основе эмпирических данных. В частности, это предполагает получение тестовых показателей на группах, которые явно различаются по критерию релевантного поведения, такому как фактическое выполнение данного вида работы. Разумеется, именно это выполнение и предназначен предсказывать конкретный тест, критический показатель по которому должен гарантировать безопасный, приемлемый или желаемый минимум. Ясной иллюстрацией эмпирического метода Установления критических показателей по тесту для отбора персонала служат таблицы ожидаемых результатов (expectancy tables), рассматриваемые в следующем разделе.
|
|
|
Таблицы ожидаемых результатов. Результаты теста можно также интерпретировать опираясь на критерий ожидаемого выполнения предстоящей программы обучения или работы. Такое употребление термина «критерий» соответствует сложившейся в психометрии традиции, как в тех случаях, когда говорят, что валидность теста Устанавливается относительно некоторого критерия (см. главу 1). Строго говоря, термин «критериально-ориентированное тестирование» следовало бы использовать при-
100
Часть 2. Технические и методологические принципы
менительно к этому типу интерпретации выполнения теста, тогда как другие подходы, обсуждавшиеся в предыдущем разделе, правильнее было бы характеризовать как содержательно- или предметно-ориентированные.
В таблице ожидаемых результатов приводятся вероятности различных критериальных исходов для лиц, получивших тот или иной тестовый балл. Например, если учащийся набрал 530 баллов по Тесту академической оценки (SAT) Совета колледжей, то каковы его шансы закончить первый курс определенного колледжа со средней оценкой А, В, С, D или F? Информацию такого рода можно получить, изучая двумерное распределение, связывающее значения прогнозирующих показателей (SAT) с критерием статуса студента первого курса (средней оценкой успеваемости). Если число случаев в каждой ячейке такого двумерного распределения заменить на проценты, получится таблица ожидаемых результатов, такая как табл. 3-6. В ней представлены данные, полученные при обследовании 211 учащихся 7-х классов, записавшихся на курс математики. В качестве предиктора здесь использован тест числового рассуждения из Дифференциальных тестов способностей (DAT), проведенный в конце первого семестра, а в качестве критерия — итоговые оценки по курсу математики в конце второго семестра. Корреляция между тестовыми показателями и критерием составила 0,60.
|
|
|
Таблица 3-6 Таблица ожидаемых результатов, демонстрирующая связь между показателями теста числового рассуждения (из DAT) и итоговыми оценками по курсу математики
211 учащихся 7-х классов
| Тестовый показатель | Число случаев | Процент | получивших каждую оценку | ||
| D и ниже | С | В А | |||
| 30 и выше | 22 | 5 | 0 | 36 59 | |
| 20-29 | 104 | 9 | 21 | 43 27 | |
| 10-19 | 71 | 36 | 37 | 24 3 | |
| Ниже 10 | 14 | 43 | 36 | 14 7 | |
(С упрощениями из Technical Manual for Differential Aptitude Tests, 5th ed., p. 152. Воспроизведено с разрешения Психологической корпорации. Copyright © 1992 by The Psychological Corporation)
В первой колонке табл. 3-6 приведены тестовые показатели, сгруппированные в четыре интервала, во второй — число учащихся, тестовые показатели которых попали в соответствующий интервал. Остальные цифры таблицы (по строкам) показывают процент учащихся внутри каждого интервала группирования показателей теста, получивших оценку А, В, С или D (и ниже) по окончании курса. Так, из 22 учеников, набравших в тесте числового рассуждения 30 и более баллов, 5 % получили оценку D (или ниже), никто не получил оценку С, 36 % получили оценку В и 59 % — оценку А. На другом краю распределения, из 14 учеников с тестовым показателем ниже 10 баллов получили оценку D (или ниже) 43 %, С — 36 % и В — 14 %. Аномальные 7 % учеников, получивших оценку А, представляют собой лишь один случай и потому не несут практически полезной информации для обобщения, так же как и 5 % учеников с тестовым показателем 30 (и более) баллов, получивших оценку D (или ниже), опять-таки представленных одним случаем. Тем не менее с учетом ограничений имеющихся данных, проценты в табл. 3-6 дают оценки вероятности получения индивидуумом
|
|
|
Глава 3. Нормы и смысловое значение тестовых показателей
101

Рис. 3—7. Диаграмма ожидаемого отсева, показывающая связь между выполнением заданий батареи отбора летчиков и отчислением с начального курса летной подготовки
(Из J. С. Flanagan, 1947, р. 58)
того или иного критериального балла. Например, если новый ученик наберет 24 балла по тесту числового рассуждения DAT (т. е. попадет в интервал группирования 20-29), его шансы получить А по курсу математики можно оценить как 27 из 100, а шансы получить В — как 43 из 100, и т. д.
Во многих практических ситуациях может отдаваться предпочтение дихотомическим критериям в виде «успеха» или «неудачи» в работе, в прохождении учебного курса и т. д. В этих условиях можно построить диаграмму ожидаемого отсева, показывающую вероятность успеха или неудачи для каждого интервала группирования тестовых показателей. Рис. 3-7 дает пример такой диаграммы. Базирующаяся на батарее отбора летчиков, разработанной ВВС США, эта диаграмма ожидаемого отсева показывает для каждого станаина шкалы процент курсантов, не справившихся с начальным курсом летной подготовки. Можно увидеть, что в процессе подготовки отсеялись 77 % курсантов, получивших тестовый показатель, равный 1 станаину, и только 4 % курсантов, получивших показатель, равный 9 станайнам. Между этими крайними значениями процент неудач неуклонно снижается с прибавлением каждого станаина. На основе этой диаграммы ожидаемого отсева можно было бы предсказать, например, что приблизительно 40 % курсантов с тестовым показателем, равным 4 станайнам, потерпят неудачу и приблизительно 60 % из них удовлетворительно завершат начальный курс летной подготовки. Аналогичные прогнозы по каждому станаину можно строить и относительно вероятности успеха или неудачи отдельных курсантов. Так, получив тестовый показатель, равный 4 станайнам, курсант имеет 60 шансов против 40, т. е. 3 Шанса против 2, успешно закончить начальный курс летной подготовки. Нетрудно видеть, что помимо обеспечения критериально-ориентированной интерпретации тес-
|
|
|
102
Часть 2. Технические и методологические принципы
товых показателей таблицы ожидаемых результатов и диаграммы ожидаемого отсева дают общее представление о валидности теста в предсказании по данному критерию. По этой причине эмпирические процедуры установления критических значений тестового показателя более подробно обсуждаются в конце главе 6, в разделе о моделях принятия решений в честном использовании тестов. В этом разделе также упоминаются математические методы для установления оптимальных критических значений тестового показателя при различных условиях. Кроме того, с конкретными приложениями критических показателей в основных областях психологической практики можно ознакомиться в главе 17.
НАДЕЖНОСТЬ
Под надежностью понимается устойчивость, или согласованность (consistency) результатов теста, получаемых при повторном его применении к тем же испытуемым в различные моменты времени, при использовании разных наборов эквивалентных заданий или же при изменении других условий обследования. Такое понимание надежности лежит в основе вычисления ошибки измерения отдельного показателя, благодаря чему мы можем предсказывать диапазон случайных колебаний тестового балла у конкретного человека, возникающих, вероятно, под действием посторонних или неизвестных факторов.
Понятие надежности обычно охватывает несколько аспектов устойчивости тестовых показателей. В самом широком смысле надежность теста показывает, в какой степени индивидуальные различия в тестовых показателях могут быть отнесены на счет «истинных» различий в изучаемых свойствах, а в какой могут быть приписаны случайным ошибкам. Говоря более специальным языком, меры надежности теста позволяют оценить, какую долю общей дисперсии (общей изменчивости) тестовых показателей составляет дисперсия ошибок. Это не «ошибки» в обычном смысле слова, предполагающем, что их можно было бы избежать или скорректировать путем усовершенствования методологии измерений. Данное терминологическое значение слова «ошибка» унаследовано из более ранней эпохи в развитии психологии, когда интерес ученых сосредоточивался на выявлении общих законов поведения и оценивании испытуемых по таким свойствам, которые считались неизменными базовыми чертами. В наше время психологи признают изменчивость существенным свойством всякого поведения и потому занимаются выявлением и классификацией многочисленных источников такой изменчивости.
Что касается надежности показателя, суть дела заключается в определении дисперсии ошибок. Факторы, которые применительно к одним задачам можно было бы счесть источниками случайной вариации показателя (т. е. дисперсии ошибок), при Решении других задач могут быть отнесены, и не без основания, к причинам его истинной дисперсии. Например, если бы нас интересовало измерение колебаний настроения, то происходящие день ото дня изменения в показателях шкалы «радость — уныние» были бы релевантны цели данного теста и, следовательно, составляли бы часть
104
Часть 2. Технические и методологические принципы
истинной дисперсии показателей. С другой стороны, если бы тест предназначался для измерения более устойчивых характеристик личности, те же ежедневные колебания попали бы уже в разряд дисперсии ошибок.
В сущности, любое условие тестирования, которое не имеет отношения к цели теста, представляет собой источник дисперсии ошибок. Поэтому, стремясь к поддержанию единых условий тестирования (контролируя общую обстановку, временные ограничения, инструкции испытуемым, раппорт и другие аналогичные факторы), пользователи тестов способствуют уменьшению дисперсии ошибок и повышению надежности тестовых показателей. Но и при оптимальных условиях тестирования ни один тест не является абсолютно надежным инструментом. Поэтому каждый тест следует сопровождать сведениями о его надежности. Сообщаемая мера надежности характеризует тест только в случае его проведения в стандартных условиях и с людьми, имеющими сходство с теми, кто входил в состав нормативной выборки. Следовательно, при описании теста нужно точно указывать и характеристики этой выборки, вместе с типом измеренной на ней надежности.
Теоретически, разновидностей тестовой надежности может быть очень много — столько же, сколько и условий, влияющих на показатели теста, так как любое из этих условий может оказаться нерелевантным конкретной цели тестирования и потому отнесенным к источникам дисперсии ошибок. Однако практическое применение находит лишь несколько типов надежности. В этой главе мы обсудим основные способы измерения надежности тестовых показателей, вместе с источниками дисперсии ошибок, идентифицируемыми каждым из этих способов.1
Поскольку все типы надежности касаются степени согласованности или соответствия между двумя независимо полученными множествами показателей, их все можно выразить в виде коэффициента корреляции. Соответственно, с целью разъяснить использование и интерпретацию коэффициентов корреляции, в следующем разделе рассматриваются их основные характеристики. Более специальное обсуждение корреляции, с подробным описанием вычислительных процедур, можно найти в любом элементарном учебнике по статистике для педагогов и психологов (см, например, Ru-nyon, & Haber, 1991; D. С. Howell, 1997).
Коэффициент корреляции
Смысл корреляции. По существу, коэффициент корреляции (г) выражает степень соответствия или связи между двумя множествами показателей. Например, если ис-пытуемый„получивший высший показатель по переменной 1, получает высший показатель и по переменной 2, а испытуемый, получивший второй лучший показатель по переменной 1, получает такой же показатель по переменной 2 и т. д. до самого низшего
1 Этот подход к надежности показателей иногда называли теорией надежности как обобщаемое™ (см. Brennan, 1994; Crick & Brennan, 1982; Cronbach, Gleser, Nanda, & Rajaratnam, 1972; Feldt, & Brennan, 1989; Shavelson & Webb, 1991). Однако это название недостаточно специфично для дифференциального термина, так как понятие обобщаемое™ применимо ко всем аспектам тестовых показателей, да и, фактически, ко всем научным данным. Более точная характеристика этого метода определения надежности основана на его способности идентифицировать компоненты дисперсии как релевантные или нерелевантные.
Глава 4. Надежность
105
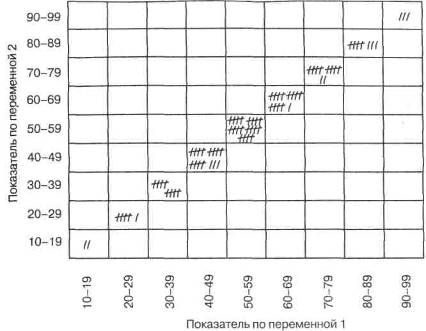
Рис. 4—1. Двумерное распределение для гипотетической корреляции (+ 1)
показателя в группе, то имеет место прямолинейная корреляция между переменными 1 и 2. Величина корреляции составляет в этом случае + 1,0.
Рис. 4-1 иллюстрирует гипотетический случай прямолинейной положительной корреляции. На рисунке представлена диаграмма рассеяния, или двумерное распределение. Каждая палочка на этой диаграмме отмечает показатель испытуемого как по переменной 1 (горизонтальная ось), так и по переменной 2 (вертикальная ось). Нетрудно заметить, что все 100 случаев в данной группе распределились вдоль диагонали, идущей из левого нижнего угла в правый верхний угол диаграммы. Такое распределение означает прямолинейную положительную корреляцию (+ 1,00), поскольку из него видно, что относительное положение каждого испытуемого по обеим переменным одинаково. На практике, чем ближе двумерное распределение показателей к этой Диагонали, тем выше положительная корреляция между ними.
На рис. 4-2 изображена прямолинейная отрицательная корреляция (— 1,00). В этом случае имеет место полная инверсия показателей по двум переменным: лучший индивидуальный результат по переменной 1 соответствует худшему по переменной 2, и наоборот, причем это обратное соотношение показателей сохраняется неизменным на всем распределении. Из диаграммы рассеяния видно, что все испытуемые Распределяются по диагонали, идущей из левого верхнего в правый нижний угол.
Нулевая корреляция указывает на полное отсутствие связи. Если положение каждого испытуемого относительно переменной 1 определить методом вытаскивания бумажек с именами из шляпы, а затем ту же процедуру повторить для переменной 2, то в Итоге мы и получим нулевую или близкую к нулю корреляцию. При этих условиях, Зная результат индивидуума по переменной 1, невозможно предсказать его относи-
106 Часть 2. Технические и методологические принципы

Рис. 4—2. Двумерное распределение для гипотетической корреляции (- 1)
тельное положение на переменной 2. Испытуемый, имеющий высший показатель по переменной 1, мог бы получить высокий, средний или низкий показатель по неременной 2. Одни испытуемые могут случайно оказаться выше или ниже среднего показателя по обеим переменным, другие будут выше среднего по одной переменной и ниже среднего по другой, иными словами, не будет никакой закономерности в связи показателей при переходе от одного человека к другому.
Вычисляемые по реальным данным коэффициенты корреляции попадают между граничными значениями (- 1 и + 1) и обычно отличаются от нуля, но практически всегда оказываются меньше единицы (по абсолютному значению). Корреляция между показателями способностей почти всегда положительна, хотя часто невысока. Когда между двумя такими переменными обнаруживается отрицательная корреляция, обычно это результат того, каким способом выражались показатели по этим переменным. Например, если временные показатели коррелировать с показателями суммарной результативности, то результатом, скорее всего, будет отрицательная корреляция. Так, если показатель каждого испытуемого по тесту арифметических вычислений выражается количеством минут, затраченных на выполнение всех заданий, тогда как показатель по тесту арифметических рассуждений представлен числом правильно решенных задач, то можно ожидать появления отрицательной корреляции между этими показателями. В данном случае наименее успевающий (работающий медленнее всех) испытуемый получит численно самый высокий показатель по первому тесту, в то время как по второму тесту самый высокий показатель будет у наиболее успевающего, т. е. решившего больше всего задач, испытуемого.
Глава 4. Надежность
10
Коэффициенты корреляции можно вычислять разными способами, в зависимости от природы данных. Наибольшее распространение получил коэффициент корреляции произведения моментов Пирсона. Этот коэффициент учитывает не только положение индивидуума в группе, но и степень его отклонения в ту или иную сторону от среднего уровня группы. Напомним, что когда положение каждого индивидуума выражается в единицах стандартных показателей, те, кто занимает положение выше среднего, получают положительные стандартные показатели, а те, кто находится ниже среднего уровня, — отрицательные. Таким образом, испытуемый, превосходящий группу по уровню обеих коррелируемых неременных, будет иметь два положительных стандартных показателя, а испытуемый, отстающий от группы по уровню этих переменных, — два отрицательных. Если теперь перемножить стандартные показатели каждого из этих испытуемых по обеим переменным, то оба произведения будут положительны. Пирсоновский коэффициент корреляции есть просто среднее арифметическое всех таких произведений. Его числовое значение бывает высоким и положительным, когда соответствующие стандартные показатели имеют по обеим переменным одинаковые знаки и приблизительно равную величину. Когда испытуемых занимают положение выше среднего по одной неременной, но ниже среднего по другой, то соответствующие произведения будут отрицательны. А если сумма произведений отрицательна, то отрицательной будет и корреляция. Когда же одни произведения отрицательны, а другие положительны, корреляция будет близка к нулю.
На практике нет необходимости переводить каждый первичный показатель в стандартный перед нахождением их произведений, так как это преобразование можно выполнить разом для всех показателей после суммирования их попарных произведений. Существует много ускоренных методов вычисления коэффициента корреляции Пирсона. Метод, представленный в табл. 4-1, не самый быстрый, но зато он лучше других раскрывает смысл коэффициента корреляции. В табл. 4-1 показано вычисление г Пирсона между показателями по арифметическому тесту и тесту чтения у 10 детей. В двух столбцах справа от имен учеников приведены их показатели по первому (X) и второму (У) тесту. Суммы и средние арифметические 10 показателей приведены под соответствующими столбцами. В третьем столбце приведены отклонения (.г) каждого показателя по арифметическому тесту от среднего арифметического этих показателей, а в четвертом — отклонения (у) индивидуальных показателей по тесту чтения от их среднего арифметического. Квадраты этих отклонений даны в следующих двух столбцах таблицы, а суммы квадратов отклонений используются при вычислении стандартных отклонений показателей по обоим тестам с помощью метода, описанного в главе 3. Вместо того чтобы каждое х и у делить на соответствующее SD Для получения стандартных показателей, это деление выполняется только раз, в конце, как показано в формуле коэффициента корреляции в нижней части табл. 4-1. Попарные произведения (ху) в последнем столбце получены перемножением соответствующих отклонений в столбцах (х) и (у). Для вычисления корреляции (г) сумма этих попарных произведений делится на число случаев (N) и па произведение двух стандартных отклонений (SDxSD,,).
Статистическая значимость. Вычисленная в табл. 4-1 корреляция (г =0,40) указывает на умеренную положительную связь между показателями арифметического тес-га и теста чтения. То есть налицо некоторая тенденция, выражающаяся в том, что дети, хорошо показавшие себя в арифметическом тесте, также неплохо справляются с тес-
108
Часть 2. Технические и методологические принципы
Таблица 4-1 Вычисление коэффициента корреляции произведения моментов Пирсона
| Ученик | Арифметика | Чтение | |||||
| X | Y | X | У | X2 | У2 | ху | |
| Билл | 41 | 17 | + 1 | -4 | 1 | 16 | -4 |
| Кэрол | 38 | 28 | -2 | + 7 | 4 | 49 | -14 |
| Джеффри | 48 | 22 | + 8 | + 1 | 64 | 1 | 8 |
| Энн | 32 | 16 | -8 | -5 | 64 | 25 | 40 |
| Боб | 34 | 18 | -6 | -3 | 36 | 9 | 18 |
| Джейн | 36 | 15 | -4 | -6 | 16 | 36 | 24 |
| Элен | 41 | 24 | + 1 | + 3 | 1 | 9 | 3 |
| РуТ | 43 | 20 | + 3 | -1 | 9 | 1 | -3 |
| Дик | 47 | 23 | + 7 | + 2 | 49 | 4 | 14 |
| Мери | 40 | 27 | 0 | + 6 | 0 | 36 | 0 |
| ∑ | 400 | 210 | 0 | 0 | 244 | 186 | 86 |
| М | 40 | 21 |

том чтения, и наоборот. Если нас интересуют результаты только этих 10 детей, мы можем принять полученный коэффициент корреляции в качестве адекватной характеристики степени связи, существующей между двумя переменными в данной группе. В психологических исследованиях, однако, обычно стремятся распространить полученный на частной выборке испытуемых результат на более широкую совокупность, представленную этими испытуемыми. Например, мы могли бы задаться вопросом, существует ли связь между арифметическими навыками и навыками чтения у американских школьников того же возраста, что и наши испытуемые. Конечно, 10 исследованных случаев — совершенно недостаточная выборка из такой совокупности, ибо на другой сравнимой по размерам выборке можно было бы получить как гораздо более низкую, так и значительно более высокую корреляцию.
Существуют статистические методы оценки вероятных колебаний от одной выборки к другой коэффициентов корреляции, средних, стандартных отклонений и любых других групповых показателей. Вопрос, обычно задаваемый по поводу коэффициентов корреляции, еще проще: отличается ли выборочная корреляция существенно от нуля? Иными словами, если в генеральной совокупности корреляция равна нулю, то могла ли полученная на нашей выборке столь высокая корреляция появиться в результате одной только ошибки выборки? Когда говорят, что корреляция значима «на 1 %-номуровне» (или «науровне0,01»),тоимеютввиду следующее:существует всего лишь один шанс из ста, что в генеральной совокупности данный коэффициент равен нулю. Из чего можно сделать вывод, что между этими двумя переменными действительно имеет место корреляция. Уровни значимости указывают на приемлемую для исследователя степень риска совершить ошибку в выводах из полученных данных. Когда говорят, что корреляция значима на уровне 0,05, то вероятность ошиб-
Глава 4. Надежность
109
ки составляет уже пять шансов из ста. В большинстве психологических исследований применяются 1 и 5 %-ный уровни значимости, хотя при необходимости или желании можно пользоваться и другими уровнями значимости.
Вычисленная в табл. 4-1 корреляция, равная 0,40, незначима даже на уровне 0,05, что вполне ожидаемо, поскольку по 10 случаям трудно вывести общую закономерность, касающуюся связи между переменными. Для выборки такого объема самая малая корреляция, значимая на уровне 0,05, равна 0,63. Любая корреляция ниже этой величины оставляет без ответа вопрос о том, коррелируют ли эти две переменные в совокупности, из которой была извлечена выборка. Минимальные значимые (на 1 и 5 %-ном уровнях) коэффициенты корреляции для выборок разного объема можно определить по справочным таблицам значимости коэффициентов корреляции, имеющимся в любом приличном учебнике статистики. Однако для понимания проблематики этой книги требуется лишь общее представление об основных статистических понятиях.
В течение многих лет уровни значимости были традиционным средством оценивания корреляций. Тем не менее сейчас все больше сознаются недостатки этого подхода и его несоответствие потребностям исследователей. Доказательство того, что коэффициент надежности (или любая корреляция) значимо отличается от нуля, мало что дает как для теории, так и для практики. Даже высокая корреляция, когда она получена на малой выборке, не удовлетворяет «критерию значимости». Приходящий на смену уровням значимости и завоевывающий все большее признание подход учитывает фактическую величину полученной корреляции и оценивает границы доверительного интервала, в который — на выбранном уровне доверительной вероятности — попадает значение генерального коэффициента корреляции (см., например, Carver, 1993; J. Cohen, 1994; Hunter, & Schmidt, 1990; Olkin, & Finn, 1995; Schmidt, 1996; W. W. Tryon, 1996). Это смещение интереса к доверительным интервалам как дополнению, если не замене проверки значимости, предвещает важный сдвиг в анализе коэффициентов корреляции в ближайшие годы.
Коэффициент надежности. Коэффициенты корреляции широко применяются в анализе психометрических данных. Одно из применений таких коэффициентов — это измерение надежности теста. Пример коэффициента надежности, вычисленного пир-соновским методом произведения моментов, приведен на рис. 4-3. В этом случае рассчитывалась корреляция между показателями 104 человек по двум эквивалентным формам теста «беглость речи».' В обоих случаях испытуемым давалось пять минут, в течение которых они должны были написать как можно больше слов, начинающихся на заданную букву. Формы теста отличались друг от друга лишь задаваемой буквой. Авторы теста подобрали начальные буквы с таким расчетом, чтобы трудность заданий была примерно одинаковой.
Корреляция между числом слов, написанных в ходе выполнения каждой из двух форм данного теста, оказалась равной 0,72, т. е. довольно высокой и значимой на уровне 0,01. При объеме выборки N = 104 любая корреляция от 0,25 и выше является значимой на этом уровне. И все же полученная корреляция несколько ниже, чем это Желательно для коэффициентов надежности, обычно превышающих 0,80 и даже 0,90.
Одного из субтестов Тестов первичных умственных способностей для возраста 11-17 лет, разработанных SRA. Данные получены в исследовании Анастази и Дрейка (Anastasi & Drake, 1954).
no
Часть 2. Технические и методологические принципы

Показатели по тесту «беглость речи» (форма 1)
Рис. 4-3. Коэффициент надежности 0,72 (по данным из статьи Anastasi & Drake, 1954).
Диаграмма рассеяния для этих данных (рис. 4-3) представляет типичное двумерное распределение, соответствующее высокой положительной корреляции. Можно видеть, как «палочки» (условные значки для кодировки испытуемых или, в общем, наблюденных случаев) теснятся вблизи диагонали, идущей из левого нижнего в правый верхний угол; тенденция группировки в этом направлении выражена довольно определенно, хотя и наблюдается некоторый разброс отдельных случаев. В следующем разделе обсуждается использование коэффициента корреляции для вычисления различных мер надежности теста.
Типы надежности
Ретестовая надежность. Самый очевидный и понятный метод определения надежности результатов теста — его повторное проведение. В этом случае коэффициент надежности (гп) просто равен корреляции между показателями, полученными теми же испытуемыми в каждом из двух случаев проведения теста. Дисперсия ошибок соответствует случайным колебаниям в выполнении заданий от одного сеанса тестирования к другому. Эти колебания могут отчасти быть результатом неконтролируе-
Глава 4. Надежность
111
мых условий тестирования — таких, как резкие изменения погоды, внезапные шумы и другие отвлекающие факторы или, скажем, сломавшийся некстати карандаш. В какой-то степени они могут быть вызваны и изменениями в состоянии самих тестируемых — например болезнью, утомлением, эмоциональным напряжением, беспокойством, недавними приятными или неприятными переживаниями и т. д. Ретестовая надежность показывает, в какой степени результаты теста можно распространить на различные случаи его применения. Чем выше надежность, тем менее чувствительны тестовые показатели к случайным суточным изменениям состояния тестируемых и обстановки тестирования.
Приводя в руководстве к тесту его ретестовую надежность, всегда следует указывать, в каком интервале времени она измерена. Поскольку ретестовые корреляции постепенно снижаются по мере увеличения этого интервала, для любого теста существует не один, а бесконечное множество ретестовых коэффициентов надежности. Желательно также давать некоторые сведения о событиях, происшедших за время между двумя сеансами тестирования с теми, на ком измерялась надежность теста, и касающихся их учебы, работы, семейной жизни, консультирования, психотерапии и т. д.
Кроме желательности сообщения длины интервала между двумя тестированиями, хорошо бы знать, какими соображениями направлялся выбор именно этого интервала? Можно привести немало примеров тестов, надежность которых остается высокой в течение нескольких дней или недель, но спустя десять-пятнадцать лет их результаты уже практически не коррелируют с первоначальными. Так, многие из тестов интеллекта для дошкольников дают достаточно устойчивые показатели на протяжении дошкольного периода, но совершенно бесполезны в качестве инструментов предсказания IQ в позднем детстве или во взрослости. На практике, однако, чаще всего следуют простому правилу в установлении границ ретсстового интервала. Обычно дисперсия ошибок тестового показателя определяется кратковременными, случайными колебаниями, происходящими в интервалах от нескольких часов до нескольких месяцев. Поэтому, при проверке этого типа тестовой надежности, стараются придерживаться небольших временных интервалов. При тестировании маленьких детей этот период должен быть еще короче, чем у испытуемых старшего возраста, поскольку в первые годы жизни связанные с возрастным развитием изменения наблюдаются ежемесячно и даже быстрее. В целом, для любого типа обследуемых лиц ретестовый интервал, по-видимому, редко превышает шесть месяцев.
Какие-либо дополнительные изменения в относительном выполнении теста одними и теми же людьми, происходящие в более длительные промежутки времени, уместнее относить к кумулятивным и прогрессирующим, а не к чисто случайным. Кроме того, такие изменения, вероятно, характеризуют более широкую сферу поведения, чем та, которая проявляется при выполнении данного теста. Так, общий уровень способности человека к обучению, пониманию технических устройств или искусства мог за 10 лет существенно измениться вследствие каких-то произошедших с ним неординарных событий. Его статус с годами мо
|
|
|


