 |
Категории традиционных шифров. Шифры подстановки
|
|
|
|
Категории традиционных шифров
Мы можем разделить традиционные шифры с симметричным ключом на две обширные категории: шифры подстановки и шифры перестановки. В шифре подстановки мы заменяем один символ в зашифрованном тексте на другой символ; в шифре перестановки – меняем местами позиции символов в исходном тексте.
Шифры подстановки
Шифры подстановки или же моноалфавитные шифры всегда изменяют символ в исходном тексте на одну и ту же букву (или символ) в зашифрованном тексте независимо от его позиции в тексте.
Самым простейшим моноалфавитным шифром является аддитивный шифр, его иногда называют шифром сдвига, а иногда – шифром Цезаря, но термин аддитивный шифр лучше показывает его математический смысл. Предположим, что исходный текст состоит из маленьких букв (от а до z) и зашифрованный текст состоит из заглавных букв (от А до Z). Чтобы обеспечить применение математических операций к исходному и зашифрованному текстам, мы присвоим каждой букве числовое значение (для нижнего и верхнего регистра), как это показано на рисунке 8.
На рисунке 8 каждому символу (нижний регистр или верхний регистр) сопоставлено целое число из Z26. Ключ засекречивания между Алисой и Бобом – также целое число в Zn. Алгоритм кодирования прибавляет ключ к символу исходного текста; алгоритм дешифрования вычитает ключ из символа зашифрованного текста. Все операции проводятся в Zn.
Рисунок 8 – Представление букв исходного текста и зашифрованного в Z26
Рисунок 9 показывает процесс шифрования и дешифрования.
Рисунок 9 – Аддитивный шифр
Мы можем легко показать через формулу (3), что шифрование и дешифрование являются инверсными друг другу, потому что исходный текст, созданный Бобом (P1), тот же самый, что и тот, который передан Алисой (Р).
|
|
|
(3)
Аддитивные шифры уязвимы к атакам только зашифрованного текста, когда используется исчерпывающий перебор ключей (атака грубой силы). Множество ключей аддитивного шифра очень мало - их только 26. Один из ключей, нулевой, является бесполезным (зашифрованный текст будет просто соответствовать исходному тексту). Следовательно, остается только 25 возможных ключей. Ева может легко начать атаку грубой силы зашифрованного текста.
В мультипликативном шифре алгоритм шифрования применяет умножение исходного текста ключом, а алгоритм дешифрования применяет деление зашифрованного текста ключом, как показано на рисунке 10. Обратите внимание, что ключ должен принадлежать набору Zn* – это гарантирует, что шифрование и дешифрование инверсны друг другу.
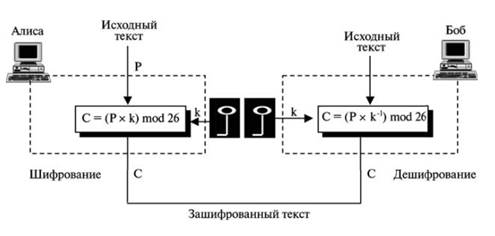
Рисунок 10 – Мультипликативный шифр
В аффинном шифре идёт комбинация мультипликативного и аддитивного шифров с парой ключей.
Первый ключ применяется мультипликативным шифром, второй - аддитивным шифром. Рисунок 11 доказывает, что аффинный шифр - фактически два шифра, применяемые один за другим. Мы могли бы показать только одну комплексную операцию, рассчитываемую по формуле (4) для шифрования или дешифрования.
и 
(4)
Однако мы использовали временный результат (Т) и указали две отдельных операции, показав тем самым, что всякий раз, когда мы используем комбинацию шифров, нужно убедиться, что каждый из них имеет инверсию на другой стороне линии и что они используются в обратном порядке в шифровании и дешифровании.
Если сложение - последняя работа в шифровании, то вычитание должно быть первым в дешифровании.
При аффинном шифре отношение между исходным текстом Р и шифрованным текстом С определяется по формуле 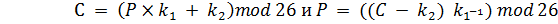(5).
|
|
|
(5)
где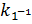 
мультипликативная инверсия 
, a 
- аддитивная инверсия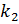 
Рисунок 11 – Аффинный шифр
Помимо моноалфавитных шифров также существуют многоалфавитные шифры. В многоалфавитной подстановке каждое появление символа может иметь различную замену. Отношения между символом в исходном тексте и символом в зашифрованном тексте - «один ко многим». Например, «A» может быть зашифровано как «D» в начале текста, но как «N» - в середине. Многоалфавитные шифры имеют преимущество: они скрывают частоту появления символа основного языка. Ева не может использовать статистическую частоту отдельного символа, чтобы взломать зашифрованный текст.
Чтобы создать многоалфавитный шифр, мы должны сделать каждый символ зашифрованного текста зависящим от соответствующего символа исходного текста и позиции символа исходного текста в сообщении. Это подразумевает, что наш ключ должен быть потоком подключей, в которых каждый подключ так или иначе зависит от позиции символа исходного текста, который используется для выбора подключа шифрования. Другими словами, мы должны иметь ключевой поток 
, в котором ki применяется, чтобы зашифровать і-тый символ в исходном тексте и создать і-тый символ в зашифрованном тексте.
Автоключевой шифр
Чтобы понять зависимость ключа от позиции, обсудим простой многоалфавитный шифр, названный «автоключевым». В этом шифре ключ - поток подключей, в котором каждый подключ используется, чтобы зашифровать соответствующий символ в исходном тексте. Первый подключ - определенное заранее значение, тайно согласованное Алисой и Бобом. Второй подключ - значение первого символа исходного текста (между 0 и 25). Третий - значение второго символа исходного текста. И так далее.
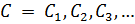
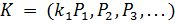
Шифрование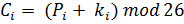 
Дешифрование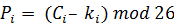 
Название шифра, автоключевой, подразумевает, что подключи создаются автоматически в зависимости от символов шифра исходного текста в процессе шифрования.
Одноразовый блокнот
Одна из целей криптографии – идеальная секретность. Исследования Шеннона показали, что идеальная секретность может быть достигнута, если символы исходного текста зашифрованы с помощью ключа, выбранного случайно из некоторой области ключей. Например, аддитивный шифр может быть легко взломан, потому что используется один и тот же ключ. Но даже и этот шифр может быть идеальным, когда ключ, который применяется для шифрования каждого символа, выбран случайно из множества ключей (00, 01, 02… 25): если первый символ зашифрован с помощью ключа 04, второй символ - с помощью ключа 02, третий - с помощью ключа 21, и так далее. Атака «только для зашифрованного текста» становится невозможна. Если передатчик изменяет ключ, используя каждый раз иную случайную последовательность целых чисел, другие типы атак также будут невозможны.
|
|
|
Эта идея реализована в шифре, который называется одноразовым блокнотом. Его изобрел американский инженер Вернам. В этом шифре ключ имеет ту же самую длину, что и исходный текст, и выбран совершенно случайно.
Одноразовый блокнот - идеальный шифр, но его почти невозможно реализовать коммерчески. Если ключ каждый раз генерируется заново, как Алиса может сообщать Бобу новый ключ? Для этого каждый раз нужно передавать сообщение. Однако есть некоторые случаи, когда возможно использование одноразового блокнота. Например, если президент страны должен передать полностью секретное сообщение президенту другой страны, он может перед посылкой сообщения передать с помощью доверенного посланника случайный ключ.
|
|
|
