 |
1.3. Криптосистемы. Определение. Суперувеличение кортежа
|
|
|
|
1. 3. Криптосистемы
Ранцевая криптосистема
Первая блестящая идея относительно криптографии открытого ключа доступа принадлежит Меркелю и Хеллману – она изложена в их ранцевой криптосистеме. Хотя эта система ненадежна в соответствии с сегодняшними стандартами, главная ее идея дает возможность понять современные криптосистемы с открытым ключом. Если нам говорят, какие элементы заранее определенного множества чисел мы имеем, то можно легко вычислить сумму чисел. Если нам говорят сумму, то трудно сказать, какие элементы «находятся в ранце».
Определение
Предположим, что нам даны два k-кортежа,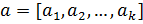 
и 
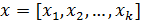. Первый кортеж - заранее определенное множество; второй кортеж, в котором х равен только 0 или 1, определяет, какие элементы а должны быть отброшены в ранце. Сумма элементов в ранце предоставлена в формуле 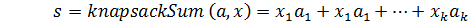(6).
(6)
По данным а и х просто вычислить s. Однако по данному s трудно найти х. Другими словами,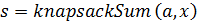 
вычисляется просто, но 
труден. Функция knapsackSum - односторонняя функция, если а - общий k – кортеж.
Суперувеличение кортежа
Просто вычислить knapsackSum и inv_knapsackSum, если k-кортеж суперувеличивается.
В суперувеличивающемся кортеже 
. Другими словами, каждый элемент (кроме а1) больше или равен сумме всех предыдущих элементов. В этом случае мы вычисляем knapsackSum и inv_knapsackSum, как показано на рисунке 19. Алгоритм inv_knapsackSum запускается от наибольшего элемента и продолжает процесс к наименьшему. В каждой итерации он проверяет, находится ли элемент в рюкзаке.
Рисунок 19 – Алгоритм knapsackSum и inv_knapsackSum
Секретная связь с использованием ранца
Посмотрим, как Алиса может передать секретное сообщение Бобу, использующему ранцевую криптосистему. Идея показана на рисунке 20.
|
|
|
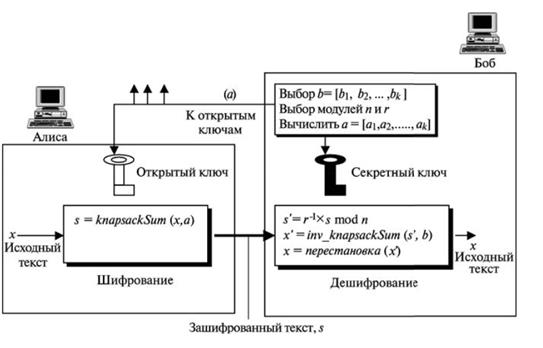
Рисунок 20 – Секретная связь с использованием ранца
Криптографическая система RSA
Самый общий алгоритм открытого ключа доступа – криптографическая система RSA, названная по имени его изобретателей Ривеста, Шамира, Эделмана.
RSA применяет два типа ключей - е и d, где е - открытый, a d - секретный. Предположим, что Р - исходный текст и С - зашифрованный текст. Алиса использует формулу (7), чтобы создать зашифрованный текст С из исходного текста P; Боб использует формулу (8), чтобы извлечь исходный текст (файл), переданный Алисой.
(7)
(8)
Модулей n создается очень большое количество с помощью процесса генерации ключей.
Для шифрования и дешифрования применяют возведение в степень по модулю. При использовании быстрого алгоритма возведение в степень по модулю выполнимо в полиномиальное время. Однако нахождение модульного логарифма так же сложно, как и разложение числа по модулю. Для него нет алгоритма с полиномиальным временем. Это означает, что Алиса может зашифровать сообщение общедоступным ключом (е) в полиномиальное время. Боб также может расшифровать его в полиномиальное время (потому что он знает d). Но Ева не может расшифровать это сообщение, потому что она должна была бы вычислить корень е-той степени из С с использованием модульной арифметики. Рисунок 21 показывает идею RSA.
Рисунок 21 – Сложность операций в RSA
Рисунок 22 показывает общую идею процедуры, используемой в RSA.
Рисунок 22 – Шифрование, дешифрование и генерация ключей в RSA
RSA использует возведение в степень по модулю для шифрования/дешифрования. Для того что бы атаковать закрытый текст, Ева должна вычислить 
.
|
|
|
Алгоритмы шифрования и дешифрования RSA представлены на рисунках 23, 24 соответственно.
Рисунок 23 – Алгоритм шифрования RSA
Рисунок 24 – Алгоритм дешифрования
Криптосистема Рабина
Криптосистема Рабина (М. Rabin) является вариантом криптосистемы RSA. RSA базируется на возведении в степень сравнений. Криптосистема Рабина базируется на квадратичных сравнениях, и ее можно представить как криптографическую систему RSA, в которой значениям е и d присвоены значения 
и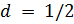 
. Другими словами, шифрование — 
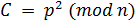и дешифрование —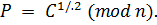 
Открытый ключ доступа в криптосистеме Рабина - n, секретный ключ является кортежем (р, q). Каждый может зашифровать сообщение, используя n, но только Боб может расшифровать сообщение, используя p и q. Дешифрование сообщения неосуществимо для Евы, потому что она не знает значения р и q. Рисунок 25 показывает шифрование и дешифрование.
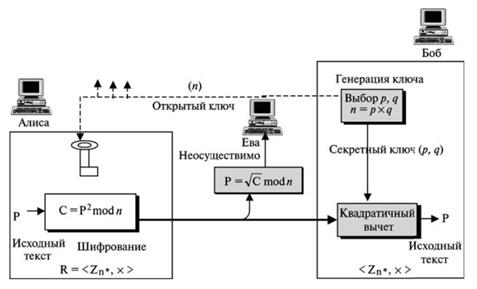
Рисунок 25 – Шифрование, дешифрование и генерация ключей
Алгоритмы генерации ключей, шифрования и дешифрования представлены на рисунках 24, 25, 26 соответственно.
Рисунок 24 – Алгоритм генерации ключей для криптосистемы Рабина
Рисунок 25 – Алгоритм шифрования в криптосистеме Рабина
Рисунок 26 – Алгоритм дешифрования
|
|
|
