 |
Показатели качества переходного процесса
|
|
|
|
На переходные процессы в системах управления накладываются определенные ограничения, связанные с особенностями их работы.
Рассмотрим основные показатели качества систем управления, пользуясь характеристикой переходного процесса отработки единичного задающего воздействия g(t)=1(t), показанной на рис.6.2.
Рис. 6.2. Характеристики переходного процесса
при типовом единичном воздействии
Для оценки качества работы системы введены следующие показатели.
1. Максимальное отклонение управляемой величины, соответствующее времени tm, от установившегося значения:
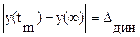, (6.16)
где tm - время установления первого максимума управляемой величины, характеризующее скорость изменения ее в переходном процессе.
Представляет собой динамическую ошибку Dдин, определяющую точность системы в переходном процессе.
2. Перерегулирование, равное отношению максимального значения управляемой величины в переходном процессе к установившемуся значению:
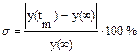. (6.17)
Перерегулирование характеризует склонность системы к колебаниям, то есть близость системы к колебательной границе устойчивости. В конечном итоге характеризует запасы устойчивости. Считается, что запас устойчивости достаточен, если s лежит в пределах от 10 до 30%.
3. Время регулирования (протекания переходного процесса) tр. Позволяет оценить быстродействие системы управления.
Учитывая, что полное затухание в системе происходит лишь при t®¥, длительность переходного процесса ограничивают тем моментом времени, когда
, (6.18)
где D - допустимое значение установившейся ошибки, обычно составляющее ±5% от y(¥).
4. Число колебаний управляемой величины y(t) за время регулирования tр. Это число составляет обычно 2¸3.
|
|
|
5. Собственная частота колебаний системы w0 = 2p/T0, где T0 - период собственных колебаний системы.
6. Логарифмический декремент затухания системы dс, характеризующий быстроту затухания колебательного процесса,
dс = ln 
, (6.19)
где ai и ai+1 - две амплитуды для рядом расположенных экстремумов кривой переходного процесса.
7. Максимальная скорость отработки управляемой величины
= tgn.
Для каждой системы управления, имеющей колебательный переходный процесс, на основе указанных критериев качества можно установить область допустимых отклонений управляемой величины.
В системах автоматического управления возможны переходные процессы, характер протекания которых отличен от указанного на рис.6.2. Все многообразие переходных процессов в системах автоматического управления можно разделить на четыре группы:
колебательный процесс, характеризуемый несколькими значениями колебаний управляемой величины за время регулирования;
малоколебательный процесс, т.е. переходный процесс с одним колебанием;
монотонный процесс, когда скорость изменения управляемой величины не меняет знака в течение всего времени регулирования (dy/dt³0 при 0£ t£tр);
апериодический процесс (без перерегулирования), когда y(t)<y(¥) c точностью до D при всех t.
Таким образом, чтобы оценить качество работы системы управления, необходимо иметь ее переходную характеристику, для нахождения которой применяются различные способы:
а) классическое математическое решение дифференциального уравнения D(p)y(t)=Q(p)1(t);
б) операционный метод: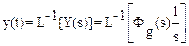 
;
в) численные и графические способы;
г) моделирование системы;
д) экспериментальная запись.
Если задающее воздействие на входе линейной системы отличается от единицы, то в переходном процессе изменяется только масштаб управляемой величины.
Частотные оценки качества
В инженерной практике для оценки показателей качества и построения переходных процессов в системах автоматического управления получили распространение частотные методы, разработанные В.В.Солодовниковым [7].
|
|
|
Математической основой частотных методов, устанавливающих связь между частотными характеристиками системы и качеством переходного процесса, является обратное преобразование Лапласа. Как известно, переходный процесс в системе определяется по формуле обратного преобразования Лапласа:
. (6.20)
Установлено, что если на систему действует единичное задающее воздействие, т.е. g(t)=1(t), а начальные условия являются нулевыми, то реакцию системы, которая представляет собой переходную характеристику, в этом случае можно определить как
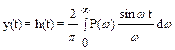, (6.21)
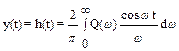, (6.22)
где P(w) - вещественная частотная характеристика замкнутой системы;
Q(w) - мнимая частотная характеристика замкнутой системы, т.е.
Фg(jw) = P(w)+jQ(w).
Выражения (6.21) и (6.22) и используются для оценок качества переходного процесса. Существует приближенный способ построения кривой переходного процесса в замкнутой системе по этим формулам с использованием h -функций.
Простейшими из частотных оценок качества переходного процесса являются запасы устойчивости, рассмотренные в разделе 5.5. Они определяют только степень близости замкнутой системы к границе устойчивости по виду частотных характеристик разомкнутой цепи.
Время регулирования и перерегулирование можно приблизительно оценить по виду вещественной частотной характеристики замкнутой системы (Рис.6.3). На основании зависимости (6.21) выведены следующие оценки. В переходном процессе получится перерегулирование s>18%, если P(w) имеет “горб”. При отсутствии “горба” будет s<18%. Процесс окажется наверняка монотонным (s=0), если dP/dw<0 и монотонно убывает по абсолютному значению. Время регулирования tр оценивается приблизительно по величине интервала существенных частот wсу, причем
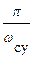< tр < 
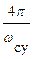. (6.23)
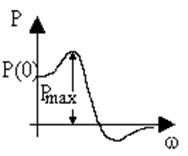
Рис.6.3. Вещественная частотная характеристика замкнутой системы
Интервал частот 0£w£wп, в котором P(w)³0, называется интервалом положительности. Интервал частот 0£w£wсу называется интервалом существенных частот, если при w=wсу и далее при w>wсу величина |P(w)| становится и остается меньше 0,05P(0). Влиянием остальной части вещественной частотной характеристики (при w³wсу) на качество переходного процесса можно пренебречь. Если же при w>wп оказывается, что |P(w)|<0,2P(0), то при оценке качества переходного процесса можно принимать во внимание только интервал положительности 0£w£wп.
|
|
|
Важно отметить, что время tр обратно пропорционально величине wсу, т.е. чем более растянута частотная характеристика, тем короче переходный процесс. Физически это связано с тем, что чем более высокие частоты “пропускает” система, тем она менее инерционна в своих реакциях на внешние воздействия.
Это же свойство позволяет связать время tр с частотой среза wс частотной характеристики разомкнутой системы. Длительность переходного процесса tр тем меньше, чем больше частота среза wс.
На основании расчетов переходных процессов по (6.21) В.В.Солодовников предложил оценивать величину перерегулирова-ния s% и время регулирования tр в зависимости от величины максимума вещественной частотная характеристика замкнутой системы Pmax, построив для этой цели номограммы (рис.6.4).
Кроме того, свойство частотных характеристик таково, что начальная их часть влияет в основном на очертание конца переходного процесса y(t), причем P(0)=y(¥). Основное же влияние на качество переходного процесса оказывает форма средней части частотной характеристики.
Рис. 6.4. Номограмма В.В.Солодовникова
В связи с этим логарифмическую частотную характеристику разомкнутой цепи системы делят на три области, причем область низких частот в основном определяет точность в установившемся режиме. Область средних частот в основном определяет качество переходного процесса. В частности, частота среза wс, как уже говорилось, определяет полосу пропускания и длительность переходного процесса. Наклон ЛАХ вблизи частоты среза характеризует колебательность переходного процесса. Так, наклон -20 дб/дек при w=wс соответствует свойствам апериодического звена, обеспечивает наименьшую колебательность переходного процесса в замкнутой системе.
|
|
|
Следующей частотной оценкой качества является показатель колебательности - максимальное значение Mmax амплитудной частотной характеристики замкнутой системы
Mmax = |Ф(jw)|max 
max. (6.24)
Чем меньше запас устойчивости, тем больше склонность системы к колебаниям и тем выше резонансный пик. Считается, что в хорошо демпфированных системах показатель колебательности не должен превосходить значений 1,1¸1,5.
Корневые оценки качества
Корневые критерии качества основываются на исследовании расположения корней характеристического уравнения замкнутой системы, то есть полюсов передаточной функции системы, а также и нулей этой передаточной функции.
Вид корней характеристического уравнения определяет характер переходных процессов в системе автоматического управления. Поэтому можно сформулировать требования по запасу устойчивости и быстродействию системы, не рассматривая самих переходных процессов, а накладывая ограничения на корни характеристического уравнения.
Для оценки быстродействия системы используется понятие степени устойчивости, являющейся простейшей корневой оценкой качества.
Под степенью устойчивости a понимается абсолютное значение вещественной части ближайшего к мнимой оси корня (рис.6.5).
Если ближайшим является вещественный корень, то такая степень устойчивости называется апериодической, так как ей соответствует апериодическая составляющая переходного процесса с1e-at. Время ее затухания характеризует общую длительность переходного процесса, так как все члены решения, соответствующие остальным корням, затухают быстрее, т.е.
tp @ 3/a. (6.25)
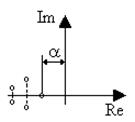
Рис. 6.5. Комплексная плоскость корней
Если ближайшем к мнимой оси окажется пара комплексных корней, то ей соответствует колебательная составляющая переходного процесса с1e-atsin(bt+b1), при этом оценка длительности переходного процесса остается прежней. Такая степень устойчивости называется колебательной.
Для оценки запаса устойчивости системы введено понятие колебательности переходного процесса.
Колебательность определяется величиной
m = ç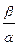 
ç, (6.26)
где a и b - вещественная и мнимая части корней характеристического уравнения. Именно эта величина характеризует быстроту затухания колебаний за каждый период T=2p/b. Чем выше колебательность, тем слабее затухание колебаний в переходном процессе.
Суммарное требование определенных значений степени устойчивости a и колебательности m приводит к области, изображенной на рис.6.6, внутри которой должны располагаться все корни характеристического уравнения замкнутой системы.
|
|
|
Далее необходимо иметь в виду, что для определения качества переходного процесса при единичном скачке задающего воздействия существенны не только корни характеристического уравнения, т.е. полюса, но также и нули передаточной функции замкнутой системы.
Рис. 6.6. Область расположения корней:
где aз и mз - заданные значения степени устойчивости и колебательности
Для уменьшения амплитуд отклонений выходной величины системы в переходном процессе желательно, чтобы нули передаточной функции замкнутой системы располагались вблизи ее полюсов.
Примером корневых оценок качества переходного процесса в системах третьего порядка является диаграмма Вышнеградского (дана в его работе 1876 г., положившей начало развития теории управления) [1,2].
Задание области расположения полюсов и нулей позволяет более полно оценить вид переходного процесса. При выборе расположения полюсов и нулей передаточной функции необходимо придерживаться общих рекомендаций [1].
1. Желательно располагать нули вблизи области расположения полюсов. Удаление нулей от полюсов ведет к увеличению амплитуд собственных колебаний в переходном процессе.
2. Для уменьшения отклонений в переходном процессе выгодно удалять полюсы друг от друга.
3. Приближение друг к другу не представляет опасности для тех полюсов, которые расположены далеко от мнимой оси.
Кроме этих рекомендаций сохраняют свою силу ограничения на область расположения полюсов, накладываемые в связи с требованием обеспечения определенного запаса устойчивости и быстродействия.
|
|
|
