 |
Перевод чисел из 10-ичной системы счисления в другую
|
|
|
|
Система счисления. Общие понятия
Система счисления – способ представления любого числа с помощью некоторого алфавита, называемого цифрами.
Число – понятие количества, величина, при помощи которой проводится счёт.
Цифра – знак для обозначения счёта.
Системы счисления бывают позиционные и непозиционные.
К непозиционным системам счисления относится римская система счисления. В этой системе значение конкретной цифры постоянно и не зависит от её расположения в записи числа. Римская система счисления слодня для вычислений. Она, в основном, используется при перечислении, нумерации.
| I | VIII | ||
| II | IX | ||
| III | X | ||
| IV | L | ||
| V | C | ||
| VI | D | ||
| VII | M |
В настоящее время используются позиционные системы счисления, в которых значимость конкретной цифры определяется её местоположением.
Общая формула представления целых положительных чисел в любой позиционной системе счисления имеет вид:
где 
– разрядный коэффициент, а 
– основание системы счисления (количество цифр, употребляемых в системе). Основание системы счисления может быть любым числом больше единицы.
При конечном значении 
количество разрядов, которое может быть представлено в данной системе счисления, ограничено, а количество 
целых положительных чисел равно 
В повседневной жизни принята десятичная система счисления (
).
Пример. 
.
Если в полученном выражении записать последовательно только выделеные цифры, отбросив весовые коэффициенты, получим сокращённую запись числа, носящую название -ичного кода числа 
В цифровой технике распространение имеет двоичная система счисления. В ней используются только две цифры: 0 и 1.
|
|
|
Кроме двоичной и десятичной, также широко используются восьмеричная и шестнадцатеричная системы счисления.
Двоичная система счисления
Двоичная система счисления – система счисления, в которой используется только две цифры: 0 и 1. Двоичная система счисления удобна для использования в цифровой технике, поскольку даёт возможность чётко различать два состояния: «включено» и «выключено» (наличие и отсутствие информации).
Число в двоичной системе счисления можно представить с помощью формулы
Для представления каждого из 10 возможных значений десятичных цифр требуется 4 разряда в двоичной системе счисления.
| Десятичные цифры | Вес разряда | |||
| 
| 
| 
| |
Восьмеричная система счисления
Достоинство восьмеричной системы счисления по сравнению с двоичной – краткость записи, т.к. запись числа в двоичной системе требует большего числа разрядов примерно в 3 раза. В ней используется цифр: от 0 до 7.
Восьмеричное число легко переводить в двоичное, и наоборот. Например, число 
. Разделим данное двоичное число на триады: 111 и 000. Определяем значение каждой триады в десятичной системе счисления: 7 и 0 соответственно. Получили запись числа в восьмеричной системе счисления: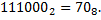 
По обратному принципу можно перевести восьмеричное число в двоичное.
Шестнадцатеричная система счисления
В 16-ричной системе счисления для отображения числа используется 16 цифр: от 0 до 15. Цифры более 9 обозначают буквами латинского алфавита.
| A | C | E | |||
| B | D | F |
16-ричная система счисления, по сравнению с 8-ричной, имеет ещё более короткую форму записи чисел.
|
|
|
Для перевода двоичного числа в 16-ричную систему счисления двоичное число делится на тетрады. Каждая тетрада представляется в 16-ричной системе счисления.
Разделим на тетрады: 0011 и 1000. Представляем каждую тетраду в 16-ричной системе счисления: 3 и 8 соответственно. 
Перевод чисел из 10-ичной системы счисления в другую
Для перевода целого числа из одной позиционной системы в другую, неоюходимо последовательно на основание новой системы 
как само число, так и частные от этого деления до тех пор, пока в остатке не получится 0. Число в новой системе счисления записывается из остатков последовательного деления основного числа и частных. Последний остаток является страшим разрядом.
|
|
|
