 |
Понятие множества. Способы задания множества
|
|
|
|
Множество – объединение различных объектов, называемых элементами множества, обладающими каким-лтбо общим свойством – предикатом.
Природа объектов множества может быть различной: галактики, атомы, буквы, числа и т.д.
Множества обозначаются заглавными буквами латинского алфавита, возможно использование индексов: 
Элементы множества обозначаются строчными буквами латинского алфавита: 
Если множество А содержит или не содержит элемент а, это записывается так:
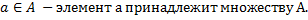
Если множество имеет несколько экземпляров одного и того же элемента, оно называется мультимножеством.
Способы задания множества:
1. Перечисление всех составляющих элементов: 
2. Установление свойства элементов множества – предиката. 
Если множество не имеет элементов, его называют пустым. Два множества называются равными, если они состоят из одних и тех же элементов.
Понятие подмножества. Универсальное множество
Часть элементов множества могут образовывать друое множество, которое называется подмножеством.
Множество, включающее в себя все подмножества некоторого множества, называется булеат (множество в степени - 
).
Универсальное множество U – множество, элементы которого есть все множества некоторой задачи или теории.
Для наглядного изображения множеств используется диаграмма Эйлера-Венна.
Операции над множествами
1. 
– объединение
2. 
– пересечение
3. 
– разность
4. 
– дополнение множества до универсального
Упорядочивание множества. Прямое произведение множеств
Во многих приложениях используются множества, в которых учитывается порядок записи элементов. Такие множеста называются упорядоченными. Самым простым упорядоченным множеством является двухэлементное множество – упорядоченная пара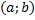 
.
|
|
|
причём 
.
Прямым (декартовым) произведением множеств А и В называется множество С, состоящее из всех упорядоченных пар 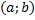таких, что 
Пузырьковая сортировка массива
Сортировка массива вставками
Сортировка массива методом Шелла
Бинарные отношения. Способы задания бинарных отношений
Бинарные отношения – отношения между двумя объектами упорядоченных пар, указывающих объекты, находящиеся в данном отношении 
. 
Левая область бинарного отношения 
– множество всех первых компонент упорядоченных пар, составляющих это отношение.
Правая область бинарного отношения 
– множество всех вторых компонент упорядоченных пар, составляющих это отношение.
Поле бинарного отношения – объединение левой и правой областей бинарного отношения. 
Способы задания бинарных отношений:
1. Перечисление всех упорядоченнных пар, входящих в данное отношение
2. Задание формулой
3. Графически
4. Таблицей пересечения
5. Матрицей
Композиция бинарных отношений
Композиция бинарных отношений R и S – бинарное отношение T, состоящее из всех упорядоченных пар 
для каждой из которых существует элемент c, принадлежащий 
, причём 
Понятие отображения множества
Отображение множества – правило, согласно которому 
соответствует единственный 
. 
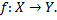
Элементы комбинаторики. Понятие выборки
Комбинаторика – ветвь математики, изучающая способы построения подмножеств некоторого конечного множества, удовлетворяющих заданным ограничениям. Такие подмножества называются выборками.
Число элементов в выборке r называется объёмом выборки.
Выборка, в которой не учитывается порядок записи, называется сочетанием. Если учитывается порядок записи, такая выборка называется перестановкой.
|
|
|
