 |
Эйлеровы и гамильтоновы графы
|
|
|
|
Цикл графа, в котором встречаются все рёбра графа, причём только по одному разу, называется эйлеровым.
Эйлеров граф можно нарисовать, не отрывая ручки от бумаги и не проходя дважды по одному и тому же ребру.
Неориентированный граф имеет эйлеров цикл только тогда, когда все его вершины имеют чётную степень.
Цикл графа, проходящий через каждую вершину только по одному разу, называется гамильтоновым.
Не существует простого критерия существования гамильтонова цикла в графе.
Элементы математической логики. Понятие простого и сложного высказывания
Основными предметами математической логики являются суждения (высказывания) и логические операции над ними.
Суждение – форма мышления, в которой утверждается или отрицается связь между предметами и их признаками или отношениями между предметами. Суждения обладают свойством выражать истину или ложь.
Суждение – связь понятий. Понятие фиксирует отдельные признаки предметов.
Всякое суждение состоит из 3-х понятий:
1. Субъект
2. Свойство (предикат)
3. Связь
Простые суждения – суждения, истинность которых можно вынести из них самих. Сложные суждения состоят из нескольких простых, соединённых логическими союзами (И, ИЛИ, НЕ, ЕСЛИ … ТО).
Логическая операция конъюнкции
| 
| 
|
Конъюнкция образует новое высказывание, которое истинно только в том случае, если все составляющие этого высказывания истинны. В противном случае высказывание ложно.
“∧”, “∙”, “&”.
Последовательное соединение ключей.
Логическая операция дизъюнкции
|
|
| 
|
Дизъюнкция образует новое высказывание, которое истинно, если хотя бы одно составляющее этого высказывания истинно. В противном случае высказывание ложно.
|
|
|
“∨”, “+”.
Параллельное соединение ключей.
Логическая операция инверсии (отрицания)
|
| 
|
Если истинно, то ложно, и наоборот.
“ 
”
Параллельное соединение ключа и лампочки.
Логическая операция импликации
|
|
| 
|
Новое высказываение ложно только тогда, когда первое составляющее этого высказывания истинно, а второе ложно.
“ 
”
Свойства конъюнкции
1. 
2. 
3. 
4. 
Свойства дизъюнкции
1. 
2. 
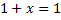
3. 
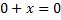
4. 
Способы задания ФАЛ
Функция алгебры логики (ФАЛ) – сложное высказываение, выраженное через совокупность простых с помощью операций логики.
1. Словесная форма
2. Таблицы истинности
3. Алгебриаческое выражение
4. Последовательность десятичных чисел
5. В виде структурной схемы
Минимизация ФАЛ при помощи карт Карно
Карта Карно – прямоугольник, разделённый на квадраты, число которых равно числу наборов аргументов рассматриваемой ФАЛ.
| 
| |
| ||
|
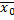
Ранг ФАЛ – количество элементов, входящих в конституенту.
Минимизация недоопределённых булевых функций.
Функция от 
переменных называется недоопределенной (НОЛФ),если она задана не на всех 
наборах. Задача минимизации такой функции заключается в оптимальном доопределении, которое позволило бы покрыть рабочие наборы минимальным количеством прямоугольников Карно, каждый из которых имел бы максимальную площадь.
Функционально-полная система булевых функций
Функционально-полной системой называется совокупность логических операций, позволяющих реализовывать логическую функцию любой сложности.
1. Штрих Шеффера
2. Стрелка Пирса
3. Исключающее ИЛИ
4. Эквивалентность (однозначность)
|
|
|
Комплексная таблица истинности для двух высказываний
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| ||
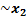
Законы де Моргана
1. 
2. 
Доказательство с помошью таблиц истинности конъюнкции и дизъюнкции.
|
|
|
