Сети Петри и их модификация

Существуют различные типы управляющих автоматов, однако независимо от структуры УА и выбранного принципа его реализации исходным материалом для проектирования УА является выполняемый в нем управляющий процесс (УП). После распределения функций между ОУ и УА и выявления взаимодействия между этими двумя компонентами управляющей системы УП может быть описан как набор процедур, соответствующих операциям технологического процесса, который определяет и порядок их выполнения.

Выбор формализованного языка, в наибольшей степени учитывающего особенности УП, является основной задачей начального этапа проектирования УА. Одно из характерных свойств УА, влияющих на структуру УП, заключается в наличии в нем множества блоков, часть которых может работать одновременно, взаимодействуя друг с другом. Поэтому формализованный язык должен прежде всего обладать средствами для описания параллелизма. Широкое распространение многопрограммных и многопроцессорных систем вызвало в свое время развитие различных языков, предназначенных для их описания и моделирования. Часть из них является расширением известных языков программирования, другие основаны на использовании различных графовых моделей. Не имея возможности дать полный обзор этих языков и провести их сравнение, рассмотрим более подробно язык сетей Петри, подучивший широкое распространение и обладающий средствами, которые позволяют в значительной степени учитывать структуру и характер функционирования управляющих автоматов.

Сети Петри разрабатывались специально для описания и моделирования систем, состоящих из отдельных взаимодействующих блоков. При этом допускается одновременная работа нескольких блоков, и данный язык отражает присущий такой системе параллелизм. Другой характерной особенностью является то, что каждый отдельный блок сам может быть целой системой, однако ее поведение возможно описать независимо от других блоков, за исключением точно определенного взаимодействия с этими блоками.

Именно такими свойствами обладают различные типы УА, так как ясно, что даже автомат с моноблочной структурой состоит из отдельных взаимодействующих компонент, что необходимо учитывать при более детальном описании УА.

Основными понятиями, на которых базируется представление рассматриваемой системы сетью Петри, являются события и условия. Событие – это некоторое действие, происходящее в системе, т.е. определенный этап вычисления или управления, выполняемый в соответствующем блоке системы. Сеть Петри описывает структуру процесса управления, она определяет последовательность процедур этого процесса и не предназначена для моделирования действительного вычисления или получения параметров управления. Для того чтобы в системе произошло определенное событие, необходимо выполнение соответствующих условий, множество которых задает состояние системы. Реализация события может привести к возникновению других условий и, следовательно, к изменению состояния системы. Такое представление системы, в качестве которой рассматриваем УА, полностью совпадает с рассмотренными ранее правилами его функционирования, что также говорит о целесообразности использования языка сетей Петри для описания УП, реализуемого в УА. Наличие уже достаточно обширной в настоящее время литературы по сетям Петри, содержащей богатую библиографию, избавляет от необходимости подробного описания этого языка, его свойств и областей применения. Поэтому дадим лишь основное определение сети Петри, введем обозначения, которые далее будут использоваться, и интерпретацию символов этого языка применительно к данной структуре УА.

В сетях Петри события и условия представляются абстрактными символами двух непересекающихся множеств – множества переходов и множества позиций, которые будем обозначать T = { t ₀, t ₁, …, t_r } и A = { a ₀, a ₁, …, a_f } соответственно. Переходы и позиции связаны между собой входной I и выходной О функциями. Функция I отображает переход t_v (v = ) в множество позиций I (t_v), которые называются входными позициями перехода. Функция О отображает переход t_v в множество позиций O (t_v) называемых выходными позициями перехода. 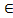Позиция a_μ является входной позицией перехода t_v, если a_μ   I (t_v),позиция a_μ — выходной позицией перехода, если a_μ  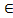 I (t_v).

Таким образом, сеть Петри является четверкой N = (А, Т, I, О), где А и Т – конечные непересекающиеся множества.

Например, простейшая сеть Петри с пятью позициями и переходами может быть задана в таком виде:

 

A = { a₀, a₁, a₂, a₃, a₄ }; T = { t₀, t₁, t₂, t₃, t₄ };

I (t₀) = a₀; I (t₁) = a₁; I (t₂) = a₂; I (t₃) = a₃; I (t₄) = a₄;

O (t₀) = a₁; O (t₁) = a₂; O (t₂) = a₃; O (t₃) = a₄;

 

Ясно, что функции I и О могут быть заданы также в виде матриц, которые называют матрицами следования и предшествования соответственно, либо в виде одной объединенной матрицы.

Наряду с приведенным способом задания сети Петри в виде системы входных и выходных функций широко используется графическое представление, которое более наглядно, но менее компактно. Граф сети Петри имеет два типа вершин, один из них соответствует позициям, обозначаемым кружочками, другой – переходам, последние обозначаются вертикальными черточками. Направленные дуги графа соединяют вершины разных типов. Если позиция a_μ является входной для перехода t_v, то дуга направлена от a_μ к t_v, если a_μ является выходной позицией перехода t_v, то дуга направлена от t_v к a_μ. В общем случае в сети Петри допускается существование кратных дуг от одной вершины графа к другой.

Таким образом, граф G = (V, W) сети Петри является ориентированным двудольным мультиграфом, где V – множество вершин; W – множество (точнее, комплект) направленных дуг. Очевидно, V = A T, A T = .

Как отмечалось, позиция сети Петри соответствует условию. Выполнение условий отмечается маркировкой позиций, так что позиция сети Петри содержит метку, если сопоставленное с ней условие выполняется, и не содержит метки в противном случае. На графе сети Петри каждая метка позиции отмечается точкой в кружке этой позиции. Однако для сетей Петри общего вида допускается наличие более одной метки в позиции, и тогда требуется иная интерпретация меток. Например, вводится понятие емкости условия, поэтому далее рассмотрим некоторые конкретные примеры использования маркированных позиций.

Маркировка сети Петри может быть задана в виде f -вектора, который определяет число меток в каждой позиции сети Петри, Таким образом, маркированная сеть Петри задается пятеркой N = (А, Т, I, О, М₀), где М₀ – вектор начальной маркировки. На рис. 7.3 приведен граф маркированной сети Петри, заданной (7.3), для М₀ = (1, 0, 0, 0, 0).

При больших значениях чисел в векторе маркировки вместо такого количества точек в позиции указывается просто их число. Точно так же при большой кратности дуг между двумя вершинами графа сети Петри указывается только одна дуга, которая помечается числом, равным ее кратности. Заметим, что часто, когда используется графическое изображение, говорят о сети Петри, опуская слово «граф».

Рис.7.3 Граф маркированной сети Петри

Распределение меток в позициях сети Петри определяет порядок ее выполнения, который зависит от последовательности реализации переходов. Переход может быть реализован, только если он становится активным. Переход является активным, когда каждая из его входных позиций содержит число меток не меньшее, чем число дуг, соединяющих ее с этим переходом. Метки, число которых равно кратности дуги, называют разрешающими. В результате реализации активного перехода удаляются разрешающие метки из всех его входных позиций, и в каждую выходную позицию помещается по одной метке для каждой дуги. Таким образом, реализация перехода заменяет маркировку сети Петри М в общем случае на новую маркировку М՛, которую называют непосредственно достижимой из М.

Из правил реализации переходов следует, что когда один переход имеет несколько выходных позиций, после его реализации все они получат метки, т.е. произойдет распараллеливание процесса. После этого активизированные параллельные участки процесса могут выполняться независимо. Переход сети Петри, имеющий несколько входных позиций, может быть реализован, только если все эти позиции содержат метки, что соответствует выполнению всех соединяющихся в данном переходе параллельных участков процесса.

Достоинством языка сетей Петри является не только то, что он позволяет описывать параллельные процессы, но и имеет средства для задания конфликтных состояний, когда необходимо запретить одновременное развитие нескольких процессов. Если позиция сети Петри содержит q меток и является входной для w > q переходов, то одновременно может быть реализовано не более q этих активизированных переходов. Вопрос о разрешении возникающего здесь конфликта, при котором одновременно несколько переходов готовы использовать метки одной и той же позиции, должен решаться дополнительными средствами.

Реализация переходов сети Петри осуществляется до тех пор, пока при очередной маркировке существует хотя бы один активный переход. Таким образом, при выполнении сети Петри возникают две связанные последовательности – реализуемых переходов и маркировок М₀, М₁, М₂.... Маркировка сети Петри определяет ее состояние, так что можно говорить как о векторе маркировки, так и о состоянии сети Петри, которое соответствует состоянию задаваемого ей процесса.

Следует иметь в виду, что в первоначально разработанном в 1962 г. доктором Петри языке, т.е. в оригинальных сетях Петри, запрещалось существование кратных дуг между позициями и переходами и вектор маркировки мог содержать лишь 0 и 1. Кроме того, реализация активного перехода разрешается только в том случае, если ни одна из его выходных позиций не содержит меток. Очевидно, тогда число меток в любой позиции не может быть больше 1. Такие позиции называют безопасными, а сеть Петри, все позиции которой безопасны, является безопасной. Она имеет простые правила выполнения и конечное число состояний, равное 2 ^f при f позициях, однако ее описательные возможности весьма ограничены. Поэтому при необходимости отразить более сложные явления, например очередь заявок или число деталей, ожидающих обработки, приходится отказываться от безопасных сетей Петри и допускать наличие нескольких меток в позиции. Если число меток в позиции не превышает некоторое значение k, то позицию называют k -безопасной или k -ограниченной. Для k ' 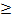  k k -безопасная позиция является и k '-безопасной. Хотя для разных позиций величина k может быть различной, всегда можно найти такое число k _макс, для которого все позиции k _макс - безопасны. Это говорит о том, что число меток в позиции ограничено, т.е. сама позиция является ограниченной. Сеть Петри называют ограниченной, если все ее позиции ограничены. Для описания многих процессов приходится использовать не только позиции, содержащие множество меток, но и допускать наличие кратных дуг между позициями и переходами.

В результате этого и сформировалась рассмотренная общая модель, в соответствии с которой сеть Петри представляется ориентированным двудольным мультиграфом с произвольной начальной маркировкой позиций и кратными дугами. Однако и эта модель является ограниченной в том смысле, что она представляет только структуру управления, но не отражает ее связь с ОУ. Поэтому появились различные расширения сети Петри, в которых по-разному моделируется взаимодействие сети Петри с управляемым процессом. Наиболее удачным можно считать подход, когда в сеть Петри вводится специальное множество позиций, каждая из которых представляет отдельный входной или выходной символ, характеризующий рассматриваемое взаимодействие. В позицию, соответствующую входному символу, метка помещается извне, а не в результате реализации переходов сети Петри. В свою очередь, метка, появившаяся при выполнении сети Петри в позиции, соответствующей выходному символу, удаляется при выполнении определенных операций в ОУ.

Другим существенным ограничением оригинальных сетей Петри является то, что реализация перехода рассматривается как мгновенное событие, занимающее нулевое время. Моделируемое таким переходом событие называют примитивным. Однако в реальном мире большинство событий занимают некоторое ненулевое время, т.е. они не являются примитивными и, строго говоря, не могут моделироваться переходами сети Петри. В связи с этим вводились различные дополнения для того, чтобы моделировать сетями Петри реальные системы с непримитивными событиями. Например, непримитивное событие может быть представлено в виде двух примитивных событий, соответствующих началу и концу непримитивного события, и условия, которое принимает истинное значение, когда происходит непримитивное событие. Другое предложение состоит в том, чтобы непримитивное событие изображать на графе сети Петри не вертикальной чертой, как примитивный переход, а прямоугольником. Но чаще такое обозначение используется в тех случаях, когда моделируются сложные иерархические системы. Тогда прямоугольником обозначается не отдельный переход, а целый уровень иерархии, который может быть представлен своей сетью Петри. При описании сетями Петри реальных систем, несмотря на введенное первоначально ограничение, обычно все же предполагается, что для реализации каждого перехода требуется некоторое время и отдельные события могут пересекаться во времени, но никаких ограничений на относительные времена реализации переходов не накладывается. В этом смысле говорят об асинхронности, одновременности и недетерминированности при выполнении сети Петри.

В последние годы на основе предложенной первоначально оригинальной модели развилась целая теория сетей Петри, в которой исследуются их модификации, различающиеся как свойствами используемых переходов, дуг, позиций и их маркировкой, так и правилами выполнения сети Петри.

Оригинальную сеть Петри называют иногда сетью позиция — переход. Если в такой сети каждый переход имеет одну входную и одну выходную позиции, сеть описывает последовательный процесс и является автоматной. Сеть Петри, в которой каждая позиция имеет один входной и один выходной переходы, является маркированным графом, который задает параллельно-последовательный процесс без разветвлений. Если выполняются свойства автоматной сети и маркированного графа, то такая сеть Петри описывает последовательный линейный процесс, в котором нет ни параллельных участков, ни альтернативных ветвей.

Следует отметить, что если переходы имеют несколько входных и выходных позиций, то сеть Петри описывает не только параллелизм, но и ожидание. Необходимым условием реализации перехода является лишь наличие разрешающих меток в его входных позициях.

Более интересными и необходимыми для описания реальных систем являются сети Петри с предикатами на переходах. В такой сети каждому переходу ставится в соответствие предикат, определяющий отношения между некоторыми переменными. Активизированный переход может быть реализован только при истинном значении сопоставленного с ним предиката. Дальнейшее расширение описательных возможностей сети Петри состоит в том, что каждому переходу сопоставляется некоторое действие, или операция. В зависимости от свойств рассматриваемой системы или процесса каждая операция может иметь разный содержательный смысл. В простейшем случае используются операции над множеством переменных, от которых зависит значение предиката. В таких сетях Петри типа предикат – действие переход реализуется, если он активизирован и сопоставленный с ним предикат имеет истинное значение, при этом неделимым образом выполняется соответствующая переходу операция и создается новая маркировка сети Петри.

Таким образом, сетью Петри оказалось возможным описывать процессы и системы, которые выполняют какие-то действия. Очевидно, эти действия занимают некоторое время, которое желательно ввести в формализованное описание процесса. Для этого было предложено два подхода. Первый из них используется во временных сетях Петри, где каждому переходу ставится в соответствие определенный интервал времени, равный длительности его реализации, т.е. продолжительности сопоставленной с ним операции. Когда переход становится активным, он сразу же переходит в стадию реализации, захватывая метки входных позиций и запрещая тем самым реализацию других конфликтующих с ним переходов. По истечение времени реализации перехода его выходные позиции получают метки.

Второй подход состоит в том, что каждому переходу ставится в соответствие пара величин а и b таких, что 0 a b. Если переход t активизирован в момент времени q, то он не может быть реализован ранее, чем в момент (q + a), и должен быть реализован до или в момент (q + b), если только условия его активизации не изменились из-за реализации других переходов. Такие сети Петри называют тайм-аутными, их используют для описания и проверки протоколов вычислительных сетей, в которых применяется механизм тайм-аута, и для описания систем со свойством восстановления. Временные сети Петри в большей степени предназначены для оценки времени выполнения исследуемого процесса.

В рассмотренных сетях Петри все метки, содержащиеся в позициях, являются одинаковыми, поэтому для того, чтобы задать разные типы условий, объектов или ресурсов, которые характеризуют состояние системы, необходимо соответственно увеличивать число позиций сети. Избежать этого позволяют так называемые помеченные сети Петри, или сети с раскрашенными позициями. В таких сетях каждой метке сопоставляется определенный признак (цвет), так что одна позиция сети Петри может содержать метки разных цветов. Теперь для активизаций перехода его входная позиция должна содержать метки с определенными признаками, которыми помечается дуга, направленная от позиции к переходу.

Обобщением сетей предикат – действие с раскрашенными позициями являются численные сети Петри. В этих сетях метки позиций могут иметь любую природу и величину, условия активизации и результат реализации перехода независимы, при реализации переходов изменяется как маркировка его входных и выходных позиций, так и содержимое памяти данных. Каждая входная дуга помечается условием активизации и условием реализации перехода, которые могут не совпадать, т.е. не все метки, необходимые для активизации перехода, удаляются из входной позиции после его реализации. На каждой выходной дуге указывается, сколько меток и с какими признаками помещаются в выходную позицию в результате реализации перехода. Переходу может сопоставляться некоторый предикат и операция над данными. Очевидно, такие сети обладают большими описательными возможностями, но слишком сложны для анализа и преобразования реальных процессов.

Другая разновидность сетей Петри использует дуги разных типов. При этом различают простые дуги, к которым относятся активизирующая, сдерживающая, входная, выходная, и составные дуги – это активизирующая входная и сдерживающая выходная. Активизирующая дуга приводит к реализации перехода, когда позиция заполнена, и запрещает его, когда позиция пуста. Сдерживающая дуга запрещает реализацию перехода, если позиция содержит метку, и активизирует его, если позиция пуста. Входная дуга удаляет метку из позиции при реализации перехода; если позиция была пуста, она остается неизменной. Выходная дуга помещает метку в позицию после реализации перехода; если позиция была заполнена, она остается неизменной. Активизирующая входная дуга является обычной дугой оригинальной сети Петри: для активизации перехода в позиции должна быть метка, которая удаляется после его реализации. Сдерживающая выходная дуга также соответствует правилам выполнения оригинальной сети Петри: для реализации активного перехода необходимо, чтобы его выходная позиция была пуста, она заполняется меткой после реализации перехода.

Введение сдерживающих дуг позволяет осуществлять проверку на нуль значения какой-либо переменной, что существенно расширяет описательные возможности сетей Петри и в этом смысле приближает их к машинам Тьюринга. Однако большинство вопросов анализа самих сетей Петри со сдерживающими дугами для неограниченных позиций становится неразрешимым.

Таким образом, выбор из существующего множества разновидностей сетей Петри той модели, которая наиболее адекватно описывает рассматриваемую систему и, обладая необходимыми описательными возможностями, сама может быть проанализирована, является достаточно сложной задачей.

Сравнение разных модификаций сети Петри позволило выделить те их свойства, которые необходимы для описания управляющих процессов и разработать некоторую обобщенную модель для описания УП общего типа. Основной задачей при этом было отразить в исходном описании структуру и свойства управляющего автомата и максимально сохранить простые правила выполнения и анализа оригинальной сети Петри.

Предыдущая123456789Следующая

Поделиться:

Воспользуйтесь поиском по сайту: