Управляющие процессы и их формализованное описание

 

Описание управляющего процесса (УП), реализуемого в УА, может быть осуществлено лишь после того, как определено назначение УА и его структура, т.е. число и состав ФБ, выполняемые ими функции и их взаимодействие. При этом полнота получаемого описания зависит как от имеющихся в распоряжении проектировщика сведений об УП, так и от цели, которую он преследует, составляя описание процесса. Для решения некоторых задач достаточно знать только общую структуру процесса, для других требуется задавать взаимодействие процедур процесса с ресурсами. Составление полного описания, которое необходимо иметь при построении УА, обычно является сложной итеративной процедурой, позволяющей постепенно выявлять и уточнять характер взаимодействия ФБ УА.

Структура УА, содержащиеся в нем ФБ и порядок их работы определяются свойствами УП, которые, в свою очередь, зависят от характеристик технологического процесса. Очевидно, используемый формализованный язык должен обладать средствами для описания различных типов УП.

Простейшим можно считать последовательный линейный процесс. Такой процесс состоит из некоторого числа процедур А₀, А₁,..., A_k, последовательность выполнения которых определяется технологическим процессом и не зависит от значений и изменений каких-либо параметров управляемой системы. Управляющий автомат, реализующий линейный процесс, содержит ОФБ, последовательность включения которых задает УП.

Считая выполнение процедуры некоторым событием и сопоставив поэтому каждой процедуре переход сети Петри, линейный УП можно описать оригинальной сетью Петри, которая будет содержать t ₀, t ₁,..., t_k переходов и a ₀, a ₁,..., a_f позиций. Появление метки в позиции а₀, соответствующее активизации процесса, вызывает последовательную реализацию всех переходов сети Петри. Хотя такое описание УП возможно, оно мало отражает действительный характер функционирования УА, поскольку в оригинальной сети Петри все переходы являются примитивными, т.е. предполагается, что они реализуются мгновенно. В действительности каждая процедура имеет определенную длительность, так что можно выделить отдельные ее фазы: начало, выполнение и окончание процедуры. Это соответствует включению, работе и отключению ОФБ, в котором выполняется процедура.

Рис.7.4 Подсеть Петри

Такую процедуру A_i можно представить подсетью Петри (рис. 7.4, а), содержащей переходы t _{н i} и t_ki и дополнительные позиции z_i и w_i, которые в отличие от внутренних позиций назовем внешними, так как их маркировка зависит не только от состояния сети Петри, но и от внешних событий. В результате реализации перехода t _{н i} который определяет начало выполнения процедуры A_i, появляются метки в его внешней z_i и внутренней a_i выходных позициях. Первая из них соответствует включению ОФБ _i, вторая – тому, что происходит событие, состоящее в выполнении процедуры А _i. Окончание работы ОФБ _i отмечается появлением метки во внешней входной позиции перехода t_ki. Этот переход реализуется, в результате чего появляется метка в его внутренней выходной позиции, означающая завершение процедуры A_i.

Следует отметить, что при многопрограммном принципе реализации УП такое описание взаимодействия с ОФБ не только наглядно и удобно, но и необходимо, так как позволит разделить переходы t _{н i} и t_ki. Как уже отмечалось, ОФБ может иметь местное управление, что позволяет ему после получения включающего сигнала работать автономно. В это время могут выполняться процедуры других процессов, которым сопоставлены свои переходы. При этом переходы t _{н i} и t_ki уже не являются переходами, связанными отношением непосредственного следования. Использование внешних выходных и входных позиций позволяет отразить специфику многопрограммного управления.

Однако разделение позиций на внутренние и внешние достаточно условно, поскольку, расширив рамки рассматриваемого явления, можно перевести часть внешних позиций во внутренние. Так, в нашем случае описания взаимодействия с ОФБ работу этого блока можно представить как непримитивное событие и промоделировать непримитивным переходом _i. Если теперь включить этот переход в рассматриваемую сеть Петри, то внешние позиции z_i и w_i станут внутренними, так как заполнение их метками и удаление меток будет связано только с реализацией переходов этой сети Петри (рис. 7.4, б).

В тех случаях, когда выполнение процедуры можно рассматривать как неделимое событие, для упрощения графа сети Петри ее фрагмент, содержащий переходы t _{н i}, _i, t_ki и позиции z_i, a_i, w_i, целесообразно представить одним переходом t _д, отметив его индексом сопоставленной с ним процедуры tⁱ _д (рис. 7.4, в). Такой отмеченный переход будем называть длительным. Следует иметь в виду, что в отличие от примитивного для реализации длительного перехода требуется некоторое время, в течение которого уже нет метки в его входной позиции, но еще не появилась метка в выходной позиции. Никаких ограничений на длительность реализации, перехода не накладывается, известно только, что это время конечно. При необходимости можно вновь заменить длительный переход подсетью Петри (рис. 7.4, б).

Реализация длительных переходов связана с использованием соответствующих ОФБ, которые являются ресурсами, необходимыми для выполнения процесса. Кроме ОФБ в состав УА могут входить элементы памяти и регистры для хранения промежуточных данных, вентили, шины передачи данных и управляющих сигналов и др. Все аппаратурно-программные средства, необходимые для выполнения процедур процесса, будем называть функциональными ресурсами (ФР). Функциональный ресурс назовем собственным ресурсом процедуры A_i, если он используется только этой процедурой и не доступен для других. Функциональный ресурс назовем разделяемым, если он может потребоваться нескольким процедурам. При описании процесса будем рассматривать только разделяемые ФР, так как именно они могут влиять на ход развития процесса.

Пусть для выполнения процедур УП необходимо l функциональных разделяемых ресурсов С ₁, С ₂,.., С _l. Если, имеется q экземпляров одного и того же ФР (например, q одинаковых ОФБ), то этот ресурс имеет кратность q (С _l ^q) и может использоваться одновременно α q процедурами. Когда q =1, ресурс имеет два состояния: «свободен» и «занят». В общем случае ресурс имеет q +l состояние.

Ресурсы, которые разделяются только процедурами рассматриваемого процесса, назовем внутренними или собственными ресурсами этого процесса. Далее будем считать, что все ФР являются внутренними.

Для выполнения процедур линейного процесса необходимы только функциональные ресурсы, и каждую процедуру А _i, такого процесса можно охарактеризовать следующими тремя множествами: { C _в ⁱ } – множество ФР, которыми процедура А _i уже владеет; { C _з ⁱ } – множество ФР, которые процедура А _i еще запрашивает; { C _о ⁱ } – множество ФР, которые освобождаются после выполнения А _i.

Если, например, для процедуры А _i { C _в ⁱ } = С₁, { C _з ⁱ } = С₃, С₄ и { C _о ⁱ } = С₁, С₄, т.е. А _i ({С₁},{С₃, С₄},{С₁, С₄}), это означает, что при выполнении процедуры А _i, ей уже предоставлен ресурс С₁, еще необходимы ресурсы С₃ и С₄, а в результате ее выполнения ресурсы С₁ и С₄ освобождаются.

Рис.7.5 Сеть Петри для процесса с пятью последовательно выполняемыми процедурами

Будем считать, что процедура не запрашивает повторно тот ресурс, который ей предоставлен в результате выполнения других процедур, поэтому { C _з ⁱ } { C _в ⁱ } = . В частном случае, когда все необходимые ресурсы запрашиваются данной процедурой и сразу освобождаются, { C _в ⁱ } =  и { C _з ⁱ } = { C _о ⁱ }. Очевидно, во время выполнения процедура владеет всеми запрошенными ресурсами. Пусть перед началом выполнения процесса и после его окончания все ресурсы свободны.

Функциональному ресурсу С_ј поставим в соответствие позицию с_ј сети Петри и назовем ее ресурсной позицией. Если q_j – кратность ФР С_ј, позиция с_ј в начальной маркировке содержит q_j меток. Позиция с_ј должна быть входной позицией длительного перехода t _д ⁱ , если C_j { C _з ⁱ }, и выходной позицией этого перехода, если C_j { C _о ⁱ }. Ясно, что когда ресурс С_ј занимается только на время выполнения процедуры A_i, то позиция С_ј является одновременно входной и выходной позицией перехода t _д ⁱ.

Таким образом, сеть Петри, описывающая линейный последовательный процесс, содержит длительные переходы t _д ⁱ, основные внутренние а _μ и ресурсные внутренние с_ј позиции. Будем считать, что заданное количество и распределение ресурсов позволяют последовательному процессу развиваться от начальной процедуры А₀ до конечной А _k.

На рис. 7.5 приведен пример сети Петри для процесса, со стоящего из пяти последовательно выполняемых процедур A ₀, A ₄, A ₁, A ₂, A ₃ при следующем распределении трех ФР С ₁, С ₂, С ₃: A ₁({ С ₂}, {-}, {-}); A ₂({ С ₂}, { С ₁}, { С ₂}); A ₃({ С ₁}, { С ₃}, { С ₁, С ₃}); A ₄({-}, { С ₂, С ₃}, { С ₃}).

Рис.7.6 Сеть Петри, задающая параллельный линейный процесс

Рассмотрим особенности описания параллельного линейно го процесса. Такой УП может иметь сложную параллельно-последовательную структуру, определяемую управляемым технологическим процессом. Сеть Петри, задающая параллельный процесс, кроме длительных переходов, соответствующих процедурам, содержит примитивные переходы для распараллеливания процесса и объединения его параллельных участков. Эти переходы будем называть соответственно переходами распараллеливания t_R и соединения t_S, число таких переходов зависит от структуры УП.

Участок процесса, соответствующий части сети Петри, заключенной между двумя последовательными переходами распараллеливания и (или) соединения будем называть элементарным подпроцессом. Такие подпроцессы могут быть параллельными либо последовательными, но в пределах одного элементарного подпроцесса все процедуры выполняются последовательно и его подсеть не содержит переходов распараллеливания и соединения.

Функциональные ресурсы, которые используются только процедурами одного и того же элементарного подпроцесса, будем называть собственными ФР этого подпроцесса. При описании процесса учитывают лишь ресурсы, разделяемые разными параллельными подпроцессами.

На рис. 7.6 приведен пример сети Петри, задающей параллельный линейный процесс при следующем распределении ФР, используемых процедурами параллельных подпроцессов:

A ₁({ С ₁}, { С ₃}, {-}); A ₂({ - }, { С ₃}, { - }); A ₃({ С ₃}, { С ₂}, { С ₃}); A ₄({ С ₁, С ₂}, { - }, { С ₁}); A ₅({ - }, { С ₁}, { - }); A ₆({ С ₁, С ₃}, { - }, { С ₃}); A ₇({ С ₂}, { - }, { С ₂}); A ₈({ - }, { С ₂}, { - }); A ₉({ С ₂}, { С ₁}, { - }); A ₁₀({ С ₁, С ₂}, { - }, { С ₂}); A ₁₁({ С ₁}, { - }, { С ₁}).

Рис.7.7 Сеть Петри с разделением ресурсов процедурами независимых параллельных процессов

Заметим, что разделение ресурсов процедурами независимых параллельных процессов превращает их в один процесс с параллельными подпроцессами, взаимодействующими через эти ресурсы. Сеть Петри (рис. 7.7) иллюстрирует этот случай.

Разветвленный процесс в отличие от линейного содержит не одну, а несколько последовательностей выполнения процедур, каждая из которых соответствует определенному набору значений логических условий, проверяемых в ЛФБ УА. Следует четко различать альтернативные ветви последовательного процесса и параллельные участки (подпроцессы) параллельного процесса, которые могут развиваться одновременно.

Если для сети Петри параллельного процесса характерно наличие переходов распараллеливания и соединения, имеющих несколько выходных и входных позиций соответственно, то для сети Петри разветвленного процесса характерно наличие позиций альтернативного разветвления и альтернативного соедине ния. Позиция альтернативного разветвления имеет несколько переходов-последователей, но одновременно может быть реализован только один из них. Позиция альтернативного соединения имеет несколько переходов-предшественников и получает метку в результате реализации одного из них. Следует отметить, что позиции альтернативного соединения имеются и в сети Петри процесса, содержащего циклы.

В разветвленном процессе конфликт, соответствующий позиции альтернативного разветвления, разрешается путем сопоставления каждому из конфликтующих переходов определенного набора значений логических условий. Очевидно, эти наборы должны быть ортогональны, чтобы при выполнении процесса активизировалась только одна из альтернативных ветвей.

Как уже отмечалось, проверка значений логических условий осуществляется в ЛФБ УА. По аналогии с функциональными ресурсами ресурсы системы, которые необходимы для определения последовательности процедур процесса, назовем логическими ЛР. В отличие от ФР для ЛР нужно знать не только его состояние, но и значение проверяемого в нем логического условия (ЛУ), которое может изменяться либо процедурами рассматриваемого УП, либо внешними событиями.

Пусть для выполнения процесса необходимо m ЛР D _l, D ₂, …, D_m таких, что в ЛР D _s проверяется значение логического условия p _s. Если значение логического условия p_s изменяется только процедурами УП, ЛР D_s будем называть внутренним ЛР. Рассмотрим вначале случай, когда все ЛР являются внутренними.

Каждую процедуру A_i будем характеризовать двумя множествами ЛУ:

{ P ₁ ⁱ } и { P ₂ ⁱ }: A_i ({ P ₁ ⁱ }, { P ₂ ⁱ }),

где { P ₁ ⁱ } – номера ЛУ и их значения, необходимые для выполнения процедуры A_i; { P ₂ ⁱ } – номера ЛУ и их значения, которые они приобретают в результате выполнения процедуры A_i.

Если, например, A_i ({ , p₂}, { , p₃}), то это означает, что для выполнения процедуры A_i необходимо, чтобы логическое условие p ₁ имело нулевое, а логическое условие р ₂ — единичное значение. После выполнения A_i значение логического условия p ₂ изменится и станет нулевым, а логическое условие p ₃ примет единичное значение, хотя само выполнение процедуры A_i не зависит от значения этого логического условия.

Если логическое условие p_s входит в множество { Р ₂ ⁱ }, т.е. его значение изменяется процедурой A_i, то эта процедура монопольно занимает ЛР D_s и во время ее выполнения он находится в состоянии занято. После завершения процедуры все ЛР освобождаются, в отличие от ФР, которые могут быть заняты при выполнении нескольких последовательных процедур.

Если логическое условие p_s входит только в множество { P ₁ ⁱ }, т.е. его значение просто используется для определения активной ветви процесса, то ЛР D_s занимается немонопольно. Допускается одновременно несколько таких обращений к одному ЛР, поскольку его состояние и значение проверяемого им логического условия при этом не изменяются. Это соответствует тому, что для выполнения процедуры A_i необходимо определенное значение логического условия p_s, которое не изменяется этой процедурой.

Рис.7.8

Если логическое условие р _s, входит только в множество { P ₂ ⁱ }, процедура A_i выполняется независимо от значения логического условия р _s, но после этого р _s принимает определенное значение, которое и указывается в { Р ₂ ⁱ }.

Очевидно, логическое условие р _s может входить как в { P ₁ ⁱ }, так и в { P ₂ ⁱ }. Это соответствует тому, что выполнение процедуры A_i зависит от значения p_s и, в свою очередь, влияет на это значение, т. е. монопольно занимает ЛР D_s.

Таким образом, для описания разветвленного процесса необходимо иметь средства моделирования существующих видов взаимодействия процесса с ЛР на языке сетей Петри. Прежде всего нужно представить каждый ЛР в терминах этого языка так, чтобы задать и его состояние, и значение проверяемого им ЛУ. Для этого ЛР D_s поставим в соответствие не одну, как в случае ФР, а три позиции сети Петри d_s, d_s ¹, d_s ⁰ . Позиция d_s содержит метку, если ресурс D_s свободен, т.е. ни одна из процедур процесса не владеет им монопольно. Позиция d_s ¹(d_s ⁰) содержит метку, если логическое условие p_s, проверяемое в ЛР D_s, имеет единичное (нулевое) значение.

Самым простым дуля описания сетью Петри является случай, когда процедура A_i изменяет значение того ЛУ, от которого и зависит ее выполнение. Например, если A_i ({ p_s }, { 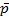_s }) и A_j ({ 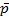_s }, { p_s }), то входными позициями перехода t _д ⁱ (t _д ^j) кроме основной внутренней позиции должны быть позиции d_s и d_s ^l (d_s и d_s ⁰ ). Выходными позициями перехода t _д ⁱ (t _д ^j) будут кроме внутренней позиции позиции d_s и d_s ⁰ (d_s и d_s ^l) (рис. 7.8, а), что соответствует освобождению логического ресурса D_s и изменению значения логического условия p_s.

Другой случай, когда выполнение процедуры A_i не зависит от значения логического условия p_s, но в результате ее выполнения p_s принимает определенное значение, также может быть промоделирован существующими средствами сети Петри. Поскольку ЛР монопольно занимается на время выполнения A_i, позиция d_s является входной позицией перехода t _д ⁱ. Так как перед выполнением A_i значение ЛУ p_s не проверяется, необходимо удалить метку из той позиции (d_s ⁰ или d_s ^l ), в которой она находилась, а затем поместить ее в d_s ⁰ (d_s ^l), если в результате выполнения A_ip_s принимает нулевое (единичное) значение, одновременно освободив ЛР D_s (рис. 7.8, б).

Наконец, третий случай, когда для выполнения процедуры A_i необходимо определенное значение ЛУ p_s, но это значение не меняется, не удается промоделировать существующими в сети Петри средствами. Кажущийся естественным способ сделать позицию d_s ^l (или d_s ⁰) входной и выходной позицией перехода t _д ⁱ не соответствует такому немонопольному занятию ЛР, когда одновременно несколько процессов могут считывать значение одного и того же ЛУ, не изменяя его.

Для описания этого взаимодействия введем в сеть Петри новый тип дуг, которые назовем неизменяющими. Если переход t_v соединен с входной позицией α_μ неизменяющей дугой, то для его реализации необходимо наличие метки в позиции α_μ, которая не удаляется из α_μ при реализации t_v. На рисунках неизменяющую дугу будем обозначать перечеркнутой стрелкой. Теперь нетрудно описать возможность немонопольного занятия ЛР, которое не приводит к изменению значения проверяемого им ЛУ. Если A_i ({ p_s }, {—}), то позиция d_s ^l должна быть соединена с t _д ⁱ неизменяющей дугой. Когда A_j ({ 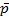_s }, {—}), позиция d_s ⁰ является входной для t _д ⁱ и соединяется с ним неизменяющей дугой (рис. 7.8, в). Заметим, что в этом случае при описании последовательного процесса метка позиции d_s не используется.

Очевидно, если A_i ({—}, {—}), то процедура A_i не взаимодействует с ЛР и переход t _д ⁱ может быть реализован независимо от маркировки позиций логических ресурсов.

Рис.7.9 Сеть Петри разветвленного последовательного процесса

Рис.7.10 Сеть Петри с альтернативными ветвями и параллельными участками

 

Рассмотренный способ представления ЛР тремя позициями сети Петри хотя позволяет промоделировать все случаи взаимодействия процессов с ресурсами, однако является достаточно громоздким, так как требует введения большого числа дополнительных позиций. Это число можно сократить, если применить так называемые сдерживающие, или тормозящие, дуги. Эти дуги были введены специально для того, чтобы использовать информацию об отсутствии метки в позиции. Если переход t_v, соединен тормозящей дугой с входной позицией α_μ, то он может быть реализован, только когда эта, позиция не содержит метку. При этом ЛР D_s можно задать двумя позициями: d_s и _s, последняя содержит метку, когда логическое условие p_s имеет единичное значение, и не содержит ее при нулевом значении этого ЛУ.

На графе сети Петри сдерживающая дуга заканчивается не стрелкой, а маленьким кружком. При использовании таких дуг взаимодействие A_i ({ p_s }, {—}) с логическим ресурсом D_s, показанное на рис. 7.8, в, будет моделироваться сетью Петри, приведенной на рис. 7.8, г.

Следует отметить, что позиции функциональных ресурсов и позиции состояний логических ресурсов могут не вводиться в описание последовательного процесса, тогда как маркировка позиций значений ЛУ может существенно влиять на развитие процесса.

На рис. 7.9 показана сеть Петри разветвленного последовательного процесса, все процедуры которого используют собственные ФР, выполнение процедур А ₁, А ₃, А ₄, А ₅, А ₆, А ₇ зависит от значений логических условий p ₁, p ₂ и процедуры А ₁, А ₃, А ₇ меняют значения логических условий: А ₁({ p _l}, { _l}); А ₃({ p ₂}, { ₂}); А ₄({ _l}, {—}); А ₅({ p _l}, {—}); А ₆( _l}, {—}); А ₇({ ₂}, { p ₂});. Для упрощения графа сети Петри не введены позиции состояний ЛР ₁ и ₂.

В общем случае управляющий процесс содержит как альтернативные ветви, так и параллельные участки; пример сети Петри такого процесса приведен на рис. 7.10. Если все логические и функциональные ресурсы УП являются внутренними, процесс можно назвать автономным, поскольку его развитие полностью определяется начальным состоянием, т. е. начальной маркировкой его сети Петри.

 

Предыдущая123456789Следующая

Поделиться:

Воспользуйтесь поиском по сайту: