 |
Влияние структуры процесса на наличие тупиковых состояний
|
|
|
|
Рассмотрим различные случаи возникновения тупиковых состояний. На рис. 7.13 приведен граф достижимых маркировок простого параллельно-последовательного процесса, заданного сетью Петри рис. 7.10. Для простоты на графе переходы будем выписывать без верхних индексов. Вначале построим граф GN в предположении, что время реализации всех переходов одинаково, поэтому одновременно активизированные переходы реализуются также одновременно. При этом процесс переходит из состояния S 2 сразу в состояние S 3. Как видно из рис. 7.13, при заданной начальной маркировке, когда ФР с1 и с2 свободны и логическое условие р 1=1, процесс, не достигнув конечного состояния, соответствующего реализации перехода t дк, попадает в состояние S 4, которое является тупиковым, так как ни один из переходов не является активным и дальнейшее развитие процесса невозможно. Таким образом, при начальном истинном значении логического условия процесс попадает в тупиковое состояние.
Аналогичный граф достижимости можно построить для начального ложного значения логического условия p 1, когда позиция 
1 в начальной маркировке не содержит метку. При этом вместо перехода t 2 будет активизирован переход t 3. Чтобы не составлять отдельные графы для различных допустимых начальных маркировок, можно построить один полный граф, предусматривающий все возможные пути развития процесса. Очевидно, при этом позиции ЛР в вершинах графа не выписываются. Такой граф для сети рис. 7.10 представлен на рис. 7.14; как видно, левая ветвь графа соответствует p 1=1 и полностью совпадает с графом рис. 7.13. При p 1=0 реализуется другая последовательность переходов, но процесс, не достигнув конечного состояния, вновь попадает в тупиковое состояние S 7. Этот граф также построен в предположении, что реализация активизированных переходов завершается одновременно. Такой граф можно назвать графом статических состояний процесса. В статическом состоянии ни один 
из переходов сети Петри не находится в стадии реализации.
|
|
|
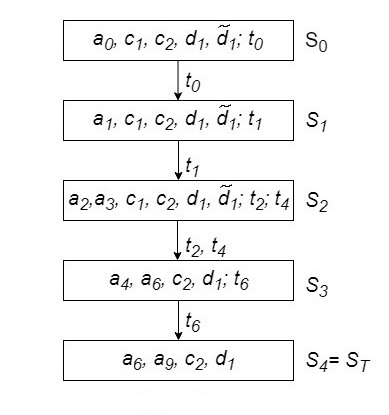
Рис. 7.13 Граф достижимых маркировок простого параллельно-последовательного процесса
Очевидно, можно построить граф, содержащий не только статические, но и все промежуточные состояния, которые возникают из-за различной скорости реализации переходов. На рис. 7.15 приведен граф, задающий полное множество достижимых состояний рассматриваемого процесса, число которых, как видно, значительно больше числа статических состояний. В таком динамическом графе исходящие из вершин дуги графа помечаются переходами, которые переходят в стадию реализации, входящие дуги помечаются переходом, закончившим реализацию. Переходы, реализация которых продолжается, записываются на этой дуге в скобках. В результате кроме статических состояний в графе появляются неустойчивые состояния; переходы, находящиеся при этом в стадии реализации, также выписываются в скобках в отличие от переходов, которые активизируются в данном неустойчивом состоянии. Следует иметь в виду, что с началом реализации перехода удаляются метки из его входных позиций, поэтому, например, в 
состоянии S 8 отсутствует метка в позиции а 3 и еще не появилась метка в позиции а 6, так как реализация перехода t 4 не закончена.
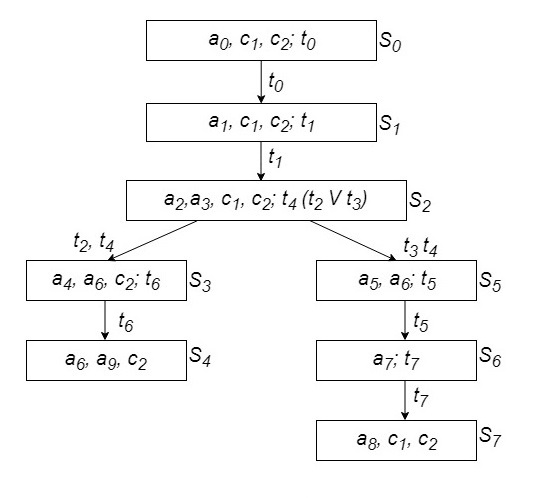
Рис. 7.14 Граф для сети Петри с альтернативными ветвями и параллельными участками
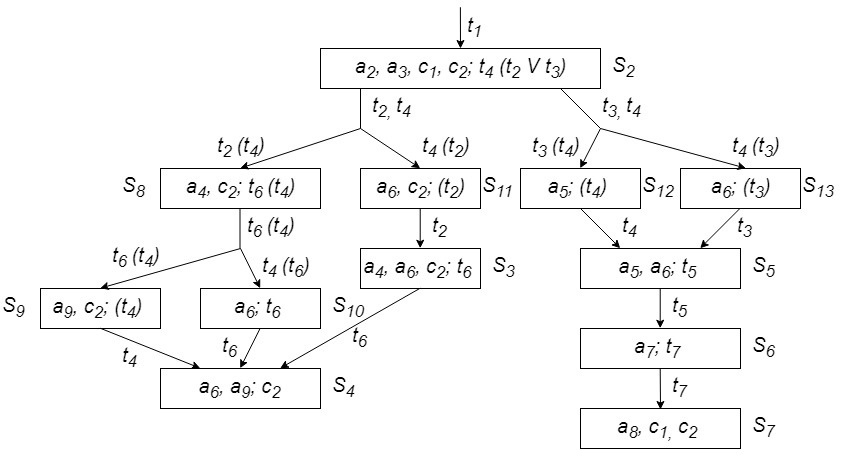
Рис. 7.15 Граф, задающий полное множество достижимых состояний
Из рис. 7.15 видно, что независимо от начального значения логического условия p 1 и относительной скорости реализации переходов, т. е. длительности соответствующих процедур, процесс, заданный сетью Петри рис. 7.10, попадает в одно из двух тупиковых состояний. Причиной этого является недопустимая структура процесса. Хотя в общем случае трудно сформулировать требования к правильной структуре процесса, некоторые обязательные условия можно указать. Необходимо, чтобы альтернативные ветви процесса имели альтернативное соединение в пределах того параллельного участка, в котором они начались. Если распараллеливание процесса происходит в одной из альтернативных ветвей, то соединение этих параллельных подпроцессов должно быть также в пределах этой ветви. Нетрудно видеть, что сеть Петри рис. 7.10 не удовлетворяет этим требованиям. Возникновение таких неприятных явлений, как ловушка, зависание, обычно также связано с нарушением указанных условий. Тупики, вызванные неправильной структурой процесса, могут быть устранены только соответствующим ее изменением.
|
|
|
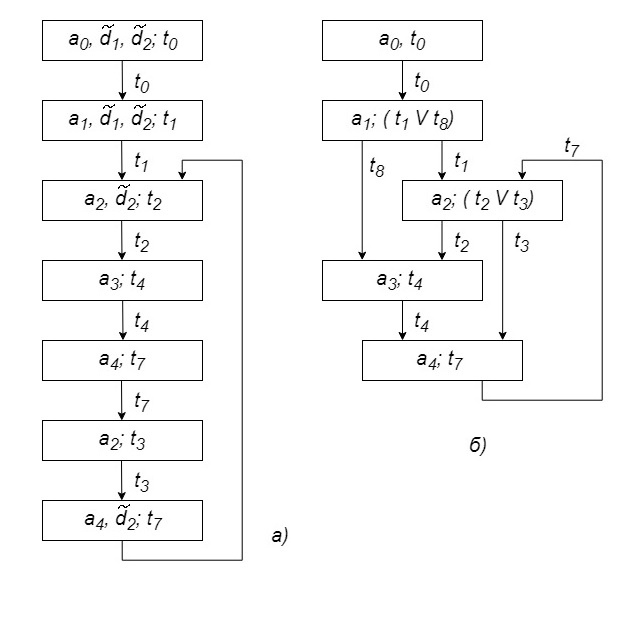
Рис. 7.16
Другой причиной недостижимости конечного состояния может быть возникновение цикла в графе достижимых маркировок. Такая ситуация свойственна не только параллельному, но и последовательному разветвленному процессу при недопустимом взаимодействии процедур процесса с ЛР.
На рис. 7.16, а приведен граф достижимых маркировок сети Петри рис. 7.9 для фиксированной начальной маркировки позиций 1 и 2. Как видно, при выполнении процесса возникает бесконечный цикл, так что заключительное состояние, связанное с реализацией перехода t 6к, оказывается недостижимым. Полный граф достижимости (рис. 7.16, б) показывает, что это состояние не достигается ни при одной из возможных начальных маркировок позиций ЛР. Таким образом, возникновение бесконечного цикла является свойством данного процесса и объясняется недопустимым взаимодействием процедур процесса с логическим ресурсом D 1. В этом случае также требуется преобразование процесса.
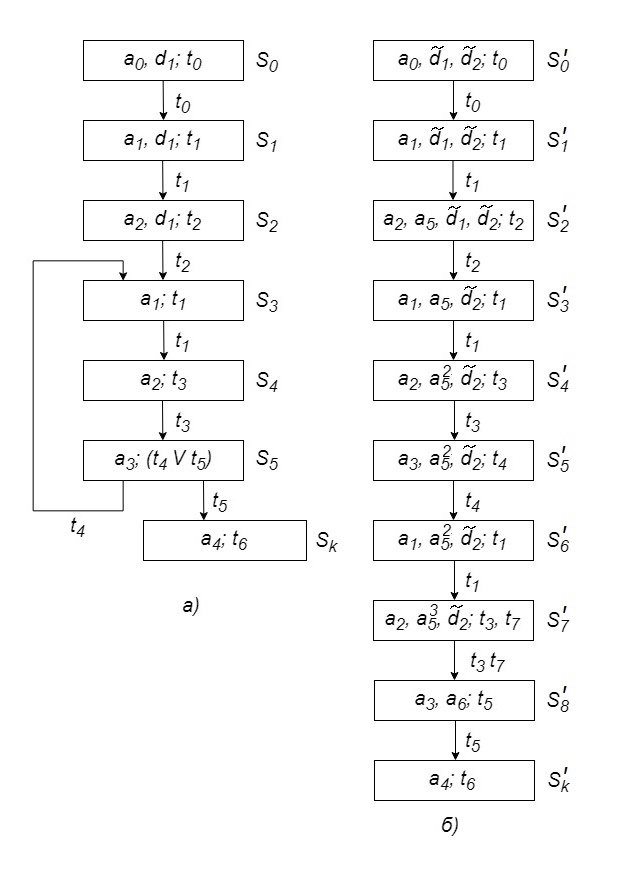
Рис. 7.17
Следует иметь в виду, что для более полного и точного анализа УП необходимо использовать всю имеющуюся в распоряжении проектировщика информацию, так как в противном случае могут быть сделаны неверные выводы о ходе развития процесса. На рис. 7.17, а приведен граф GN сети Петри рис. 7.11, а для истинного начального значения внешнего логического условия p 2. Этот граф содержит цикл, свидетельствующий о том, что если значение p 2 не изменится, процесс не достигнет конечного состояния. Поскольку здесь D 2 является внешним ЛР, неизвестно, произойдет ли такое изменение и будет ли реализован переход t 6к.
|
|
|
В сети Петри рис. 7.11, б содержится информация о функционировании логического ресурса D 2 и его взаимодействии с УП. Граф достижимости этой сети (рис. 7.17, б) показывает, что никаких циклов при выполнении процесса не возникает и конечное состояние достижимо.
|
|
|
