 |
В ячейку D8 впишите текст Сумма квадратов отклонений.
|
|
|
|
Наконец, в ячейке D9 вычислим сумму квадратов отклонений. Воспользуемся функцией СУММКВ(диапазон_ячеек_D2:D6). Для этого вызовем мастер функций, нажав на кнопку со значком fx, расположенную на панели инструментов. Появится диалоговое окно мастера функций. В списке, расположенном слева, выделим Математические функции. Затем в списке расположенном справа с помощью линии прокрутки найдем функцию СУММКВ и выделим ее. Ниже этих списков Вы видите синтаксис применения этой функции. У нее может быть несколько аргументов, разделяемых точкой с запятой. У нас таких аргументов 5 (ячейки D2 - D6). Однако, можно воспользоваться одним аргументом, указывая сразу диапазон ячеек D2:D6, содержимое каждой из ячеек должно возводиться в квадрат и суммироваться.
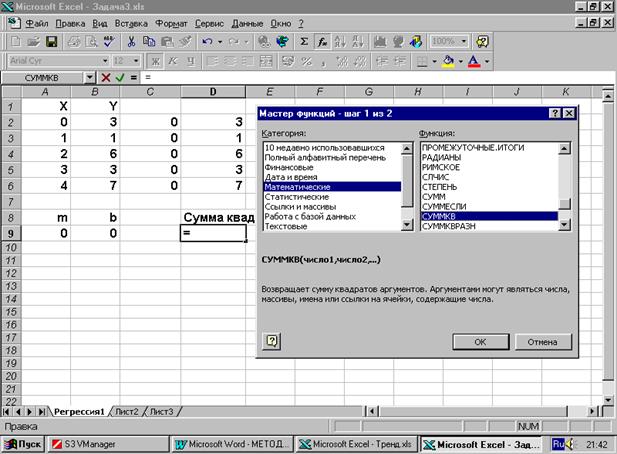
После выделения функции СУММКВ нажмите кнопку ОК. Откроется следующее окно, в котором в окошке Число 1 и следует указать диапазон ячеек D2:D6. К нашему удивлению мудрая программа уже не только сообразила, что нам нужно и не только сама вставила требуемый аргумент, но и подсчитала результат – 104 для начальных данных. Однако диапазон ячеек она указала не совсем точно. Исправьте неточность или введите в первое окошко символы $D$2:$D$6 сами. Нажмите кнопку ОК.
Окно закроется и в ячейке D9 появится результат вычисления суммы квадратов отклонений для заданных нами начальных данных m =0 и b=0, (для уравнения линии Y=0), равный 104.
Теперь все готово для решения задачи оптимизации. Выделим ячейку D9 и вызовем Решатель (меню Сервис – Поиск решения). В появившемся окне абсолютный адрес $D$9 целевой ячейки уже установлен.

Устанавливаем флажок Равной минимальному значению. Введем в окошко Изменяя ячейки абсолютные адреса $A$9:$B$9 диапазона ячеек, по которым будет минимизироваться значение целевой функции (неизвестные параметры m и b). Это можно сделать с клавиатуры, а также выделяя диапазон ячеек А9:В9 мышью. Ограничений в данной оптимизационной задаче нет.
|
|
|
Нажимаем кнопку Выполнить. Хотя процесс решения задачи еще не закончен, все вычисления уже произведены и оптимальные значения уже представлены в соответствующих ячейках. Теперь следует только подтвердить их приемлемость. В появившемся диалоговом окне Результаты поиска решения установлен флажок Сохранить найденное решение. Если это не так, то установим его сами. Если же по каким-либо причинам (например, нужно исправить допущенную ошибку или изменить числовые значения) требуется вернуться к начальным данным, то установим флажок Восстановить исходные значения.
Нажимаем кнопку ОК. Результат вычислений представлен ниже.
Таким образом, оптимальные значения коэффициентов линейной функции по критерию суммы квадратов отклонений равны m=1 и b=2. Следовательно, оптимальной является линия Y=X+2. При этом оптимальное значение суммы квадратов отклонений равно 14.

Линейная регрессия
Так как задача отыскания функциональной зависимости очень важна, в введен специальный набор функций для решения этой задачи. Эти функции основаны на методе наименьших квадратов. При этом относительно исходных данных делаются некоторые статистические предположения, а в качестве результата выдаются не только коэффициенты функции, но и ряд других статистических характеристик.
ЗАДАЧА 3. Решить задачу 2 с помощью функции, предназначенной для расчета линейной регрессии.
Решение. Для решения поставленной задачи воспользуемся статистической функцией ЛИНЕЙН.
Скопируем рабочий лист Регрессия1 предыдущей задачи на новый лист, которому дадим имя Регрессия2 (для изменения имени рабочего листа достаточно двойного щелчка на нем и последующего набора с клавиатуры). Можно просто сохранить документ Задача2 под новым именем Задача3 и ввести новое имя рабочего листа.
|
|
|
Статистическая функция ЛИНЕЙН имеет следующий вид и синтаксис:
|
|
|


