 |
После всех описанных операций рабочий лист примет следующий вид.
|
|
|
|
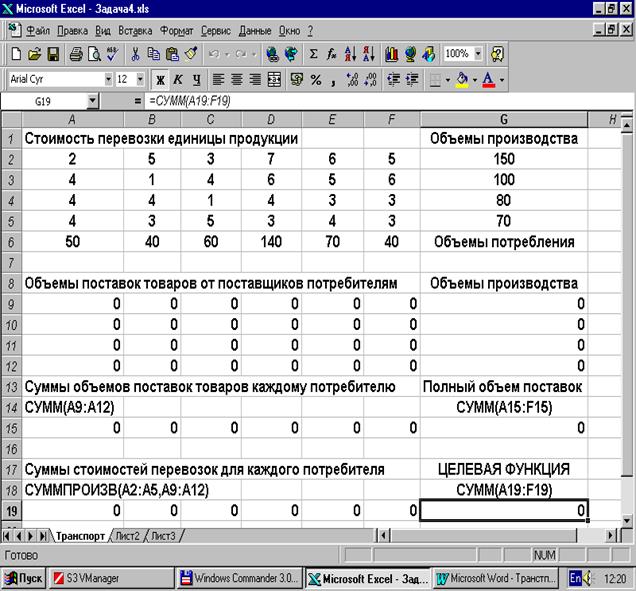
Теперь можно непосредственно приступить к решению задачи оптимизации, то есть к вычислению оптимального графика поставок, минимизирующего стоимость всех перевозок товара от поставщиков к потребителям. Активизируем (выделим) щелчком мыши ячейку с целевой функцией задачи оптимизации G19 и через меню Сервис-Поиск решения вызовем Решатель. Откроется диалоговое окно Поиск решения. В поле ввода уже записан (если нет, введите его с клавиатуры сами) абсолютный адрес $G$19 ячейки, содержащей формулу целевой функции. Поскольку в задаче требуется определить минимум целевой функции, то ниже этого поля ввода следует поставить флажок Равной минимальному значению. Переменные задачи содержатся в блоке ячеек А9:F12, поэтому в поле ввода Изменяя ячейки следует ввести абсолютные адреса $А$9:$F$12 этого блока.
Осталось ввести в алгоритм Решателя ограничения задачи. Ниже поля ввода Изменяя ячейки расположено окошко Ограничения. Однако непосредственно оно недоступно. Справа от него расположены три кнопки Добавить, Изменить, Удалить. Эти кнопки предназначены для команд на ввод и редактирование ограничений. Нажмите на кнопку Добавить.
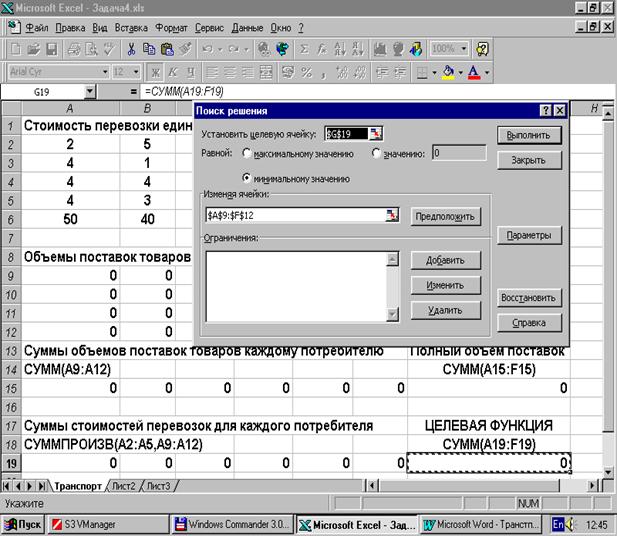
Появилось диалоговое окно Добавление ограничения. В этом окне имеются три поля ввода. Первое из них предназначено для ввода левой части ограничения. Напомним, что в соответствии с математической моделью в задаче имеются три группы ограничений: балансовые равенства для поставщиков, для потребителей и условия неотрицательности переменных. Начнем с ввода равенств для поставщиков. Суммы их поставок (объемы производства) вычисляются в ячейках G9:G12. Если требуется, перенесем, взяв мышью за строку заголовка, диалоговое окно Добавление ограничения так, чтобы стали доступны эти ячейки. Щелкнем по ячейке G9, содержащей сумму поставок первого поставщика. В первом поле ввода Ссылка на ячейку появится абсолютный адрес $G$9 этой ячейки. Во втором поле ввода требуется выбрать тип ограничения из выпадающего списка. В данном случае имеет место ограничение типа равенства, поэтому из списка выберем знак равенства =. Наконец, в третье поле ввода Ограничение нужно ввести число, определяющее объем производства V1 первого поставщика, которое при вводе исходных данных задачи попало в ячейку G2. Щелкнем мышью по этой ячейке и в поле ввода Ограничение появится абсолютный адрес $G$2. Ввод первого ограничения закончен. Если бы оно было единственным, то следовало бы нажать кнопку ОК. Однако, это не так. Поэтому нажмите кнопку Добавить.
|
|
|

После этого первое ограничение будет занесено в список Решателя, а диалоговое окно Добавление ограничения снова предстанет с чистыми полями ввода. Повторите описанную процедуру для ввода ограничения, касающегося второго поставщика, имея дело с ячейками G10 и G3. Аналогично введите третье (ячейки G11 и G4) и четвертое ограничение (ячейки G12 и G5).
Не выходя из диалогового окна Добавление ограничения, введите в список ограничений равенства для всех шести потребителей. Эти ограничения определяются парами ячеек (А15 и А6), (В15 и В6), (С15 и С6), (D15 и D6), (E15 и E6), (F15 и F6). Каждый раз вводите знак равенства и после ввода ограничения и не выходите из диалогового окна, нажимая кнопку Добавить. Делайте все это не спеша, контролируя и корректируя правильность ввода адресов ячеек.
Последнюю группу ограничений неотрицательности переменных задачи вводим аналогично. В поле ввода Ссылка на ячейку введем абсолютные адреса $А$9:$F$12 блока ячеек. Этот набор символов можно набрать с клавиатуры или с помощью мыши, охватив и выделив весь блок ячеек А9:F12 одновременно. Во второе поле ввода внесите знак неравенства >=, а в третье поле ввода впишите число 0. Теперь, поскольку введено последнее ограничения задачи, нажмите кнопку ОК.
|
|
|
В открывшемся снова диалоговом окне Поиск решения в окошке Ограничения появился весь список введенных ограничений. Используя полосу прокрутки, внимательно просмотрите их все. Если имеется ошибка или какого-либо ограничения не хватает или введено нечто лишнее, выделите нужную строку и используя кнопки Добавить, Изменить, Удалить исправьте неточность.
Теперь все готово для запуска алгоритма решения задачи линейного программирования программы Excel. Нажмите кнопку Выполнить. Спустя некоторое время в соответствующих ячейках появятся результаты вычислений и диалоговое окно Результаты поиска решения. Если все сделано правильно, результаты выглядят вполне приемлемыми, то следует согласиться с предложением Сохранить найденное решение и нажать кнопку ОК. Перед этим можно предусмотреть выдачу отчетов трех типов, в которых приведен анализ полученного решения.
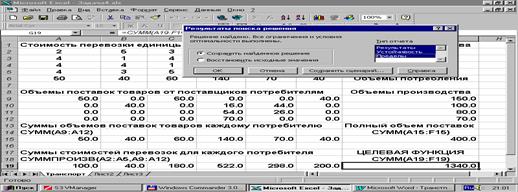
Если же сразу видно, что результаты явно неприемлемы или в ячейках появилось нечто непонятное следует установить флажок Восстановить исходные данные или нажать кнопку Отмена для того, чтобы вернуться на шаг или несколько шагов назад и исправить допущенные ошибки. В некоторых случаях поскольку решение задачи вычисляется с достаточно большой, но конечной точностью, в ячейках появляется так называемый машинный ноль – очень малое число, записанное в экспоненциальной форме, то есть в виде набора цифр, знака минус и буквы Е. Для устранения этого эффекта, следует до вычислений или после них выделить поочередно все блоки вычисляемых ячеек и через меню Формат - Ячейки в диалоговом окне Формат ячеек на вкладке Число установить формат Числовой и некоторое число десятичных знаков, например, один, два и т.д. Тогда машинные нули исчезнут, а другие результаты будут выданы с приемлемой точностью, что и сделано в данной задаче.
Мы не будем останавливаться на полученном решении задачи, само по себе оно малоинтересно, поскольку является лишь учебным примером. Отметим лишь, что все ограничения в полученной оптимальном решении выполнены и само решение очевидно оптимально.
|
|
|
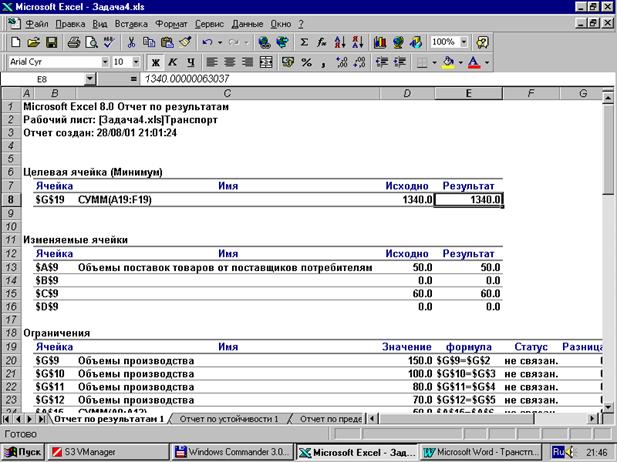
Подробное описание всей процедуры решения занимает достаточно много места и времени. Однако при некотором опыте, сам процесс решения можно выполнить за несколько минут, особенно если более широко и эффективно использовать операции копирования данных и формул. При решении реальных задач существенно большего объема это существенно сокращает время получения решения. Ниже приведен также один из отчетов, которые размещены на вставленных программой рабочих листах и полезны при анализе полученного решения.

|
|
|


