 |
Расчет доходности с заданным риском на примере портфеля Джеймса Тобина.
|
|
|
|
Используя метод Гарри Марковица в данном параграфе будет рассчитана максимально возможная доходность портфеля ценных бумаг при заданном минимально допустимом для инвестора риске. Расчеты произведены в программе Microsoft Excel. В портфель будут включены акции компаний Сбербанк, Магнит, Роснефть, Лукойл, а также безрисковые государственные краткосрочные облигации (ГКО[6]). Безрисковые ценные бумаги были введены Джеймсом Тобином[v] в портфель Марковица для снижения риска портфеля. Выбор инструментов обусловлен тем, что данные компании представлены на разных сферах рынка, а цены на акции компаний Роснефть и Лукойл сильно отличаются друг от друга, из чего можно сделать предположительный вывод, что котировки этих инструментов слабо влияют друг на друга.
|
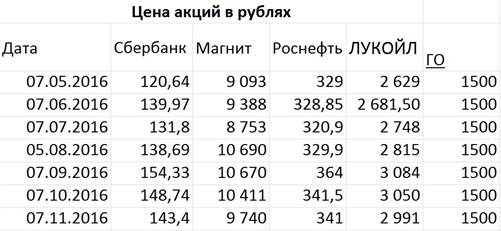
Рисунок 1. Цены на акции компаний в период с 07.05.2016 по 07.11.2016.
В данном примере были взяты котировки за полгода с месячным интервалом, что позволяет относительно точно определить ожидаемую доходность портфеля и его риск. Очевидно, что чем меньше интервал между взятыми значениями, тем точнее и объективнее получится результат. Но на рынке, где нет частых резких колебаний, интервал равный одному месяцу вполне приемлем.
|
Рисунок 2. Ежемесячная доходность акций, средняя ожидаемая доходность каждого инструмента за период и его риск.
На втором рисунке найдена ежемесячная доходность каждой акции за каждый период по формуле доходности с использованием показателей благосостояния в моменты t=0 и t=1, но здесь они представляют собой не стоимость приобретения и рыночную стоимость на момент продажи акций, а просто котировки этих акций на моменты i и i+1. Примечательно, что доходность ГО равна нулю, так как их котировки на момент i и i+1 принимают равные значения. На 07.05.2016 невозможно определить доходность за период, так как на этот день еще нет значения i+1.
|
|
|
Средняя ожидаемая доходность за период рассчитана как среднее значение ежемесячных доходностей акций компаний, а риск каждого отдельного инструмента – по финансовой функции «СТАНДОТКЛОН.В», которая показывает, насколько широко разбросаны точки данных относительно их среднего, оценивает стандартное отклонение по выборке.
Далее необходимо построить ковариационную матрицу, показывающую зависимость изменения цен акций разных инструментов друг от друга. Это делается с помощью финансовой функции «КОВАРИАЦИЯ.В», которая рассчитывает ковариацию выборки, т. е. среднее произведений отклонений для каждой пары точек в двух наборах данных.
Строку и столбец «Доля акций в портфеле» необходимо расположить именно таким образом, как показано на рисунке 3, поставив в ячейках строки нули, а в ячейках столбца значений сделать ссылки на адреса ячеек строки (т.е. поставить знак «=» и кликнуть в соответствующей ячейке строки). Это принципиально в связи с формулой расчета дисперсии: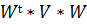 
, где V – ковариационная матрица размерностью n*n, Wt – транспонированная матрица со значениями долей акций в портфеле размерностью 1*n, a W – изначальная матрица со значениями долей в портфеле размерностью n*1. Значения долей акций компаний в портфеле располагаются в формуле таким образом так как для умножения матриц необходимо, чтобы соседние (внутренние) размерности значений совпадали.
Для расчета общей доходности и общего риска портфеля нужно задать функции в соответствующих ячейках. Для строки «общий риск портфеля» необходимо воспользоваться функцией «МУМНОЖ» дважды, так как Excel не позволяет произвести умножение трех матриц сразу. В соответствии с формулой, строка в программе должна быть заполнена следующим образом: =КОРЕНЬ(МУМНОЖ(МУМНОЖ(строка «доля акций в портфеле»;ковариационная матрица);столбец «доля акций в портфеле»)). Корень извлекается, чтобы сразу получить значение среднего квадратичного отклонения, т.е. риска, а не дисперсии.
|
|
|
|
Рисунок 3. Ковариационная матрица
Общая доходность портфеля будет находиться с помощью функции «СУММПРОИЗВ», которая перемножает соответствующие элементы заданных массивов. Первый массив – это строка «Доли акций в портфеле», а второй – найденные ранее значения средней ожидаемой доходности за период для каждого инструмента. Строка ограничение долей введена, чтобы ограничить сумму значений строки «Доля акций в портфеле» до единицы, так как сумма всех долей не может быть больше 100%.
Для того, чтобы узнать результат, необходимо вызвать функцию «поиск решения» во вкладке «данные». В строке «оптимизировать целевую функцию» нужно сделать ссылку на ячейку, соответствующую общей доходности портфеля и выбрать параметр «до максимума», а в ограничениях необходимо сделать ссылку на ячейку, соответствующую риску портфеля и указать максимально допустимое значение (в данном примере – риск меньше или равен 5%). Ячейку соответствующую ограничению долей приравниваем к единице. Важно отметить, что поиск должен быть выполнен для нелинейных задач.
|
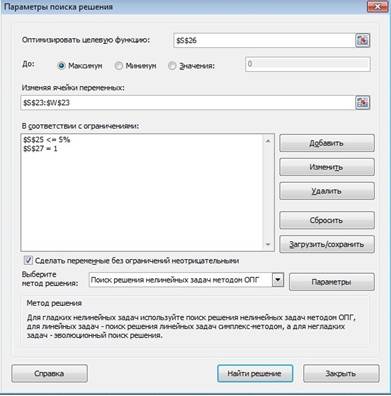
Рисунок 4. Параметры поиска решения
В результате программа выдает ответ в виде долей, в размере которых инвестор должен вкладывать деньги в акции компаний. В данном примере стоит сформировать портфель, который на 31,7% будет состоять из акций компании Сбербанк и на 68,3% - из акций компании Лукойл. Абсолютно невыгодными окажутся вложения в ГО, акции компаний Магнит и Роснефть, а общая доходность такого портфеля составит 2,5% при риске 5%.
|
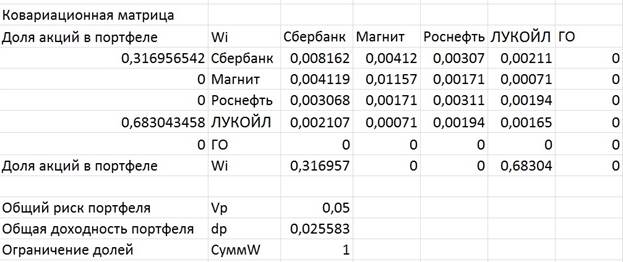
Рисунок 5. Результаты расчетов
Те же операции можно производить для нахождения минимального риска при заданной желаемой доходности, но с той лишь разницей, что в параметрах поиска решения необходимо указать минимум желаемой доходности оптимизировать риск до минимума.
Заключение.
Инвестирование в различные активы является неотъемлемой частью современного финансового мира для всех - от крупных корпораций и компаний среднего размера до домохозяйств, так как операции с ценными бумагами влияют на многие факторы. Обеспечение инвестиционной безопасности, в первую очередь – риск-менеджмен – это фундамент, без которого успешная инвестиционная деятельность невозможна. Существует множество способов управления рисками, некоторые из которых были описаны в работе. Уровень риска и сопутствующие показатели могут быть рассчитаны как с помощью арифметических операций, так и в компьютерных программах. Тем не менее, главный вывод, который можно сделать, заключается в том, что, несмотря на достижения в области экономики, математики и электроники, работа с анализом рисков до сих пор не до конца автоматизированный и сложный процесс, так как инвестиционное решение всегда связано с человеческим фактором. Кроме того, необходимо учитывать такие факторы, как рынок, на котором оперирует инвестор, возможность и обоснованность использования того или иного метода управления рисками. Успешный риск-менеджмент, а как следствие и вся инвестиционная деятельность, могут быть достигнуты только в том случае, если инвестор подкован во всех аспектах инвестирования. Управление рисками подразумевает не только знание видов рисков и методов управления ими, но и существенную математическую базу, так как понимание ситуации, в которой в определенный момент находится тот или иной инвестор не может быть достигнуто без ряда вычислений, только с помощью которых инвестор сможет понять реальную картину на рынке.
|
|
|
Литература.
1. Галанов В.А. «Рынок ценных бумаг». Учебник – ИНФРА-М. – 2006 год;
2. Теплова Т.В. «Инвестиции - теория и практика». Учебник – Юрайт – 2016 год;
3. Уильям Ф. Шарп «Инвестиции». Учебник – ИНФРА-М. – 2001 год;
4. А.И. Зимин. ИНВЕСТИЦИИ - ВОПРОСЫ И ОТВЕТЫ.. 2006
5. Колмыкова Т.С. «Инвестиционный анализ». Учебник – ИНФРА-М.-2001 год;
6. Курс лекций по дисциплине «финансовая математика» доцента кафедры информатики и математики ВАВТ Москаленко Н.Е;
7. Курс лекций по дисциплине «инвестиции» профессора кафедры менеджмента и маркетинга ВАВТ Ильиновой В.В;
|
|
|
8. http://studme.org/investirovanie/ - терминологический словарь;
9. Tass.ru/ekonomika/4066291 – Информационное агентство ТАСС «Несовершенство закона о концессиях»
[1] Value at Risk – стоимостная мера риска.
[2] Рейтинг ценной бумаги - это результат текущей оценки кредитоспособности эмитента по отношению к конкретному финансовому обязательству или конкретному финансовому проекту. Рейтинги основываются на анализе текущего финансового состояния и платежеспособности эмитента - путем изучения текущей информации, предоставляемой эмитентом или получаемой из других источников, и являются оценкой качества долговых ценных бумаг и привилегированных акций.
[3] Initial Public Offering – первичное размещение акций на бирже.
[4] Андеррайтер (от англ. underwriter – гарант, страхователь) - юридическое лицо, которое осуществляет руководство процессом выпуска ценных бумаг и их распределения.
[5] Коэффициенты корреляции и ковариации показывают только линейную зависимость.
[6] ГКО и ОФЗ (облигации федерального займа) – безрисковые и не приносят дохода, используются в портфелях для снижения уровня риска.
[i] Модель CAPM используется для того, чтобы найти требуемый уровень доходности актива, который предполагается добавить к уже существующему хорошо диверсифицированному портфелю с учетом рыночного риска этого актива.
[ii] APT – теория, которая подразумевает, что ожидаемая доходность финансового актива может быть найдена с помощью модели линейной зависимости ожидаемой доходности от макроэкономических факторов, к каждому из которых в той или иной степени будет чувствителен результат, в зависимости от bettaj-коэффициента, определяющего степень влияния факторов.
[iii] Option Pricing Model, также известная как млдель Блэка - Шоулза – модель, поределяющая теоритическую цену на опционы европейского стиля, и подразумевающая, что если базовый актив торгуется на рынке, то цена опциона на него неявным образом устанавливается самим рынком. Модель используется для всех деривативов, а также для оценки собственного капитала финансово зависимых фирм.
[iv] Гарри Макс Марковиц (р. 24 августа 1927 года) – выпускник Чикагского университета, американский экономист Калифорнийского университета Сан-Диего, лауреат Нобелевской премии по экономике (1990) «за работы по теории финансовой экономики». Его вклад в науку заключается в том, что он первый предложил использовать методику формирования инвестиционного портфеля.
[v] Джеймс Тобин (5 марта 1918 – 11 марта 2002 гг.) – американский экономист, лауреат Нобелевской премии по экономике (1981). Дополнил портфель Марковица безрисковыми ценными бумагами, что позволило уменьшить общий риск портфеля, автор налога на операции с иностранной валютой (налог Тобина), созданного с целью контроля за миграцией капитала.
|
|
|
