Игра в смешанных стратегиях

ТЕОРИЯ ИГР И ПРИНЯТИЯ РЕШЕНИЙ

ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ИГР

При решении задач экономики и последующего принятия решения приходится учитывать множество факторов различного характера, при­чем эти факторы обладают свойствами неопределенности. Следователь­но, результат принятия решения будет также составлять неопределен­ность. Например, количество проданных товаров в значительной степени зависит от спроса населения на тот или иной товар. Спрос является ве­личиной случайной и зависит от многих факторов, которые являются неопределенными.

В процессе поиска принятия решений появляются многочисленные варианты, которые приходится рассматривать, чтобы выбрать наилуч­ший из числа имеющихся. С этой целью необходимо проводить количе­ственный анализ и на его основе принимать обоснованное решение. Для обоснования принятия решений в условиях неопределенности разрабо­таны специальные математические методы и модели. Задачи принятия решений в условиях полной или частичной неопределенности решаются с помощью теории игр и статистических решений.

Теория игр — математическая (модель) теории конфликтных ситуа­ций, занимается принятием решений в этих ситуациях двумя или более противниками, каждый из которых стремится оптимизировать свои ре­шения за счет других.

Игра — это совокупность правил, определяющих сущность кон­фликтной ситуации, которые устанавливают:

а) выбор способа действия игроками на каждом этапе игры;

б) информацию, которой обладает каждый игрок при выполнении таких выборов;

в) плату для каждого игрока после завершения любого этапа игры.

Основными понятиями теории игр являются: конфликтующие сто­роны, называемые игроками, одна реализация игры — партией и набор еe возможных конечных состояний, называемых исходом игры, — это Выигрыш, ничья или проигрыш. Игрокам (участникам игры) известны Платежи в виде матрицы А = { a_ik }.

Развитие игры во времени проходит последовательно по этапам (хо­дам). Ходом в теории игр называется выбор одного из правил действия, предусмотренных игрой, и его реализацию. Ходы бывают личные и слу­чайные.

Личным ходом называют сознательный выбор игроком одного из ва­риантов действия и его осуществление.

Случайным ходом называют выбор, выполняемый не волевым реше­нием игрока, а каким-либо способом случайного выбора, например, бро­сание монеты, сдача карт, вращение барабана рулетки и т.д.

Одним из основных показателей теории игр является стратегия. Стратегией игрока называется совокупность правил, определяющих вы­бор варианта действий при каждом личном ходе этого игрока от начала до окончания игры.

Оптимальной называется такая стратегия игрока, которая при мно­гократном проведении игры обеспечивает игроку максимально воз­можный средний выигрыш или минимально возможный средний про­игрыш.

В зависимости от причин, вызывающих неопределенность исходов, игры делят на основные группы:

1. Комбинаторные игры, в которых правила позволяют каждому иг­року проанализировать все разнообразные ходы и выбрать тот из них, который ведет к лучшему исходу для этого игрока. Неопре­деленность исхода связана с тем, что количество ходов слишком велико и практически игрок не в состоянии их перебрать и про­анализировать. К таким играм относятся шахматы, шашки и др.

2. Азартные игры — это игры, источником неопределенности кото­рых являются случайные факторы. Эти игры состоят из случай­ных ходов, при анализе которых применяется теория вероятно­стей. К ним относятся рулетка, игра в кости, отгадывание стороны выпадения монеты и т.д.

3. Стратегическими играми являются такие, в которых неопределен­ность исхода вызвана тем, что каждый из игроков, принимая ре­шение о выборе предстоящего хода, не знает, какой стратегии бу­дут придерживаться другие участники игры. Такие игры изучает теория игр.

В игре могут сталкиваться интересы двух или более игроков. Если в игре участвуют два игрока, то игра называется парной, если число игро­ков больше двух, то она называется множественной.

Различают игры по сумме выигрыша. Игра называется с нулевой суммой, если один игрок выигрывает за счет другого, а сумма выигрыша одного равна проигрышу другого. Парная игра с нулевой суммой назы­вается антагонистической, так как интересы игроков прямо противопо­ложны. Наиболее полно исследованы в теории игр антагонистические игры.

В зависимости от количества возможных стратегий игры делятся на конечные и бесконечные. Игра называется конечной, если у каждого игрока имеется только конечное число стратегий. Игра называется бес­конечной, если хотя бы у одного игрока имеется бесконечное число стратегий.

По количеству ходов, которые выполняют игроки для достижения определенных целей, игры бывают одношаговые и многошаговые.

Одношаговые игры состоят в том, что игрок делает один ход. В мно­гошаговых — игроки выполняют последовательно ряд ходов согласно правилам игры.

ПОСТАНОВКА ИГРОВЫХ ЗАДАЧ

Основными вопросами теории игр являются:

1. Какие свойства стратегий следует считать признаками оптималь­ности.

2. Существуют ли стратегии игроков, которые обладали бы свойст­вами оптимальности.

3. Как определить оптимальные стратегии, если они существуют.

Рассмотрим игру двух лиц с нулевой суммой. Пусть игра состоит из

двух ходов: игрок I выбирает стратегию А_i а игрок II — стратегию В_к, а вы­игрыши и каждого из игроков удовлетворяет условию:

(9.1)

Если то

Пусть функция Составим матрицу А, в которой укажем стратегии A_i, i = (1,n) первого игрока и В_k, к = (1,n) — второго игрока (9.2).

B₁ B₂ … B_k … B_n

 

(9.2)

Строки матрицы А соответствуют стратегии А_i, столбцы — страте­гии В_k. Матрица А называется платежной или матрицей игры. Элемент a_ik платежной матрицы А является выигрышем игрока I, если он выбрал стратегию А_i, а игрок II принял стратегию В_к. Стратегии А_i и В называют­ся чистыми стратегиями игроков.

Пусть игрок I выбирает некоторую стратегию А_i, тогда в худшем случае (например, игроку II известен выбор этой стратегии). Он получит выиг­рыш, равный min a_ik, то есть минимальному элементу в строке i платеж­ной матрицы А. Учитывая такое положение, игроку I необходимо выбрать такую стратегию, чтобы максимизировать минимальный выигрыш:

(9.3)

Величина α называется нижней ценой игры, которая обеспечивает гарантированный выигрыш игрока I. Стратегия А_i обеспечивающая по­лучение такого выигрыша называется максиминной.

Игрок II при выборе стратегии В_к проиграет не более максимального значения из элементов k-го столбца, то есть величина проигрыша не боль­ше max a_ik Игрок II выберет такую величину, которая максимальный проигрыш β минимизирует, то есть

(9.4)

Величина называется верхней ценой игры, а соответствующая проигрышу стратегии — минимаксной.

Пусть выигрыш игрока I будет V, тогда его значение ограничено ниж­ней и верхней ценами игры, то есть

(9.5)

Если же значение совпадают, то есть

(9.6)

то выигрыш игрока I составляет определенную величину и игра называ­ется вполне определенной, а выигрыш (9.6) называется значением игры и равен элементу

Вполне определенные игры называют также играми с седловой точ­кой или играми в чистых стратегиях. Элемент в платежной матрице А является одновременно минимальным в строке i и максимальным в столбце k и называется седловой точкой. Седловой точке соответствуют оптимальные стратегии игроков, а их совокупность является решением игры. Решение игры показывает, что если один из игроков принимает свою оптимальную стратегию, то для другого игрока отклонение от оп­тимальной стратегии не является выгодным.

Пример 9.1

Определить нижнюю и верхнюю цены игры, оптимальные стратегии игроков и цену игры, если платежная матрица представлена в виде:

Для матрицы А введем обозначения чистых стратегий. и

для I и II игроков соответственно и укажем справа столбец минимальных значений элементов в каждой строке, то есть для max a_ik, и строку (под матрицей) для максимальных значений в каждом столбце,

ⁱ

то есть для

ⁱ

Определяем нижнюю цену игры

и верхнюю цену игры

Так как то цена игры V равна

Оптимальной стратегией игрока I является первая чистая стратегия A_1, элементы которой соответствуют первой строке платежной матрицы А, то есть А₁ = (5, 6, 4, 3). Оптимальной стратегией для игрока II будет чис­тая стратегия В₄ с элементами четвертого столбца матрицы А, то есть В₄ = = (3, 2, 1, 0).

Ответ: А₁ = (5, 6,4, 3), В₄ = (3, 2, 1,0) и α= β = V = 3.

Пример 9.2

Определить нижнюю и верхнюю цены игры, если платежная матрица А задана в виде:

Так как то седловой точки нет, и решение матричной игры в чистых стратегиях не существует. Цена игры V находится в пределах 5<V<7.

Ответ:

ИГРА В СМЕШАННЫХ СТРАТЕГИЯХ

Если платежная матрица не имеет седловой точки, то цена игры V определяется условием (9.5), то есть игрок I обеспечит выигрыш не мень­ше 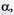а игрок II обеспечит проигрыш не больше Так как то игрок I стремится увеличить выигрыш, а игрок II — уменьшить проигрыш. Если действия игроков неизвестны, то они будут применять чистые стратегии случайным образом с определенной вероятностью. Таким образом, сме­шанная стратегия — это полный набор чистых стратегий игрока при многократном выполнении ходов в одних и тех же условиях с соответст­вующими вероятностями.

Чистые стратегии игроков в их оптимальных смешанных стратегиях называются активными.

Теорема 1. Применение оптимальной смешанной стратегии обеспе­чивает игроку максимальный средний выигрыш (или минимальный средний проигрыш), равный цене игры V независимо от действий друго­го игрока, лишь бы он придерживался своих активных стратегий.

Теорема 2. Теорема Дж. фон Неймана (основная теорема теории игр). Каждая конечная матричная игра имеет по крайней мере оптималь­ное решение в смешанных стратегиях.

Следствие. Каждая конечная игра имеет цену, величина которой яв­ляется математическим ожиданием выигрыша I игрока и проигрыша игрока II. Выигрыш — V называется ценой игры и соответствует опти­мальному решению.

Смешанные стратегии для соответствующих игроков I и II — S_: и S₂ обозначают:

(9.7)

(9.8)

где A_i и В_к — чистые стратегии игроков I и II соответственно,

(9.9)

Вероятности применения соответствующих стратегии игроками I и II, причем:

Зная платежную матрицу А, можно определить средний выигрыш (математическое ожидание) М (А, X, Y):

(9.10)

Решить матричную игру — это означает определить цену игры V и оптимальные стратегии, то есть (три числа). В ответах задач иногда опускают значения чистых стратегий, а указывают только веро­ятности соответствующие определенным чистым стратегиям.

Рассмотрим конечную игру, матрица которой имеет размер 2x2, то есть

(9.11)

Определить оптимальные стратегии игроков I и II и соответствую­щие им вероятности для матрицы (9.11), то есть

Для игрока I получаем систему уравнений

(9.12)

Для игрока II система имеет вид:

 

(9.13)

Если и игроки имеют только оптимальные смешанные страте­гии, то определитель матрицы А (9.11) не равен нулю. Следовательно, системы (9.12) и (9.13) имеют единственные решения.

Решая системы уравнений (9.12) и (9.13), находим вероятности X и У в виде:

 

(9.14)

Пример 9.3

Дана платежная матрица А:

 

Найти решение игры, то есть определить оптимальные стратегии иг­роков и цену игры.

Решение

1. Определяем нижнюю и верхнюю цены игры:

Так как то игра не содержит седловой точки и цена игры имеет значение в пределах

2. Определяем решение в смешанных стратегиях, вычисляя вероят­ности применения соответствующих стратегий игроками I и II. Запишем системы уравнений:

для игрока I

для игрока II

Решая эти системы, находим вероятности:

Ответ:

При решении игровых задач платежные матрицы в большинстве слу­чаев имеют размерность т х п, в которых то есть исходная матрица является сложной. Размерность матрицы можно сократить, ис­ключая в них дублирующие и заведомо невыгодные доминирующие стра­тегии игроков.

Дублирующими называются стратегии, которым соответствует оди­наковые значения элементов в платежной матрице, то есть матрица со­держит одинаковые строки (столбцы). Если в платежной матрице элемен­ты строки А_j, не меньше соответствующих элементов строки A_j, то строка А_i,- называется доминирующей, а строка А_j - — доминируемой. Аналогично можно определить доминирующий и доминируемый столбцы.

Игроку I невыгодно применять стратегии, которым соответствуют доминируемые строки. Игроку II невыгодно применять стратегии, кото­рым соответствуют доминирующие столбцы. При решении матричных игр можно сокращать размерность матриц, исключая из нее доминируе­мые строки и доминирующие столбцы, если такие имеются.

Для упрощения вычислений можно выполнить преобразование пла­тежной матрицы, при котором не изменяются значения вероятностей смешанных стратегий.

Теорема 3. Если являются решением платежной матрицы А, то решением игры с платежной матрицей является тройка чисел где — любое действительное число.

Пример 9.4.

Определить оптимальные стратегии игроков и величину цены игры, если платежная матрица имеет вид:

(9.15)

Решение

1. Так как стратегия А₃ является доминирующей над стратегией А₄ , то исключаем стратегию А₄ в табл. (9.15) и получаем табл. 9,16.

(9.16)

 

2. В табл. 9.16 с позиции игрока II стратегии В₃ и В₄ являются доми­нирующими, поэтому эти столбцы исключаем и получаем табл. 9.17 в виде:

(9.17)

3. Исключаем дублирующую стратегию A₃ в табл. (9.15) и получим расчетную таблицу в виде:

4. Преобразуем матрицу C₁ на основании теоремы 3, полагая k = 10 и b = -4;

(9.18)

5. Определяем нижнюю и верхнюю цены игры матрицы (9.18):

Так как то седловой точки нет.

6. Определяем решение игры в смешанных стратегиях, составляя сис­темы уравнений для соответствующих вероятностей:

для игрока I

(9.19)

для игрока II

(9.20)

 

Решая системы (9.19) и (9.21), находим вероятности:

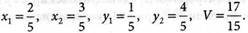
Переходим к исходной платежной матрице, вычисляя цену игры

Ответ:

123	Поделиться:

Воспользуйтесь поиском по сайту: