Сведение матричных игр к задачам линейного программирования

 

Рассмотрим матричную игру, платежная матрица которой задана в виде:

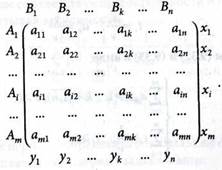(9.30)

Если размерность матрицы тхn (т > 2, п > 2) не имеет седловой точ­ки, то решение может быть получено в смешанных стратегиях в соответ­ствии с теоремой Неймана, т.е.

(9.31)

Применение игроками I и II своих оптимальных стратегий гаранти­рует игроку I средний выигрыш не меньше цены игры v, а игроку II ми­нимальный проигрыш не больше v, т.е.

для игрока I

(9.32)

 

для игрока II

 

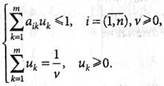
(9.33)

Таким образом, задача заключается в определении оптимальной сме­шанной стратегии S,, которая указывает для игрока I максимально воз­можный средний выигрыш, а S-ц — для игрока II минимально возможный для него проигрыш.

Разделив обе части ограничений (9.32) и (9.33) на цену игры и вводя обозначения:

(9.34)

получаем системы (9.32) и (9.33) в виде:

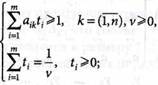
(9.35)

(9.36)

Учитывая, что игрок I стремится максимизировать (выигрыш), а игрок II пытается минимизировать v (проигрыш), переменные и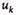

необходимо выбрать таким образом, чтобы целевая функция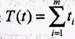

принимала минимальное значение, а целевая функция — максимальную величину.

Следовательно, решение матричной игры сводится к решению пары двойственных задач линейного программирования:

 

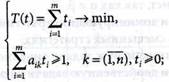
(9.37)

(9.38)

Решая задачи (9.37) и (9.38) симплексным методом, определяем зна­чения переменных t_t ки_ки целевых функций

Затем вычисляем соответствующие вероятности и цену игры для ис­ходной задачи, учитывая зависимости:

(9.39)

(9.40)

Пример 9.8.

Найти решение игры, т.е. определить оптимальные стратегии игроков и цену игры, если платежная матрица задана в виде:

 

(9.41)

Решение

1. Определяем нижнюю и верхнюю цены игры, используя максиминную и минимаксную стратегии:

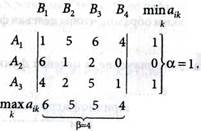
Седловой точки нет, так как

2. Дублирующих и доминирующих стратегий в платежной матрице А нет. Задачу решаем в смешанных стратегиях.

3. Сведем матричную игру к задаче линейного программирования. Составляем прямую и двойственную задачи на основании условий (9 28) и (9.38).

Прямая задача:

(9.42)

Двойственная задача:

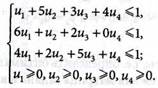
(9.43)

4. Вводим зависимые переменные , для прямой задачи и для двойственной задачи и ограничения (9.42) и (9.43) перепишем в виде:

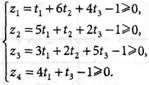
(9.44)

(9.45)

5. Решаем пару двойственных задач симплексным методом, составляя совмещенную таблицу решения двойственных задач.

Найдем независимые переменные и 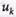и целевые функции T_min и F_max

Решаем задачу максимизации и получаем одновременно решение ми­нимизации.

Так как в табл. № 1 опорное решение (все свободные члены положи­тельны), определяем оптимальное решение (исключаем отрицательные коэффициенты в F-строке). Выполним шаг модифицированного жорданова исключения с разрешающим элементом Получаем табл. № 2.

Полученное решение (табл. № 2) не является оптимальным. Выпол­ним симплекспреобразование с разрешающим элементом , т.е. раз­решающим столбцом является коэффициент в F-строке с минимальным

значением, а в качестве разрешающей строки берем строку с ми­нимальнымзначением отношений.

 

 

 

Решение задачи, представленное табл. № 3, является опорным и оп­тимальным. Выписываем значение переменных и функций из табл. № 3:

 

 

Определяем соответствующие вероятности смешанных стратегий игроков и цену игры на основании (9.39) и (9.40):

Ответ:

 

ИГРА С ПРИРОДОЙ

Матричная игра двух лиц, у которой действия одного из игроков яв­ляются случайными, а возможные стратегии определяются как ее состоя­ние, называются играми с природой.

Например, природой можно считать условия погоды в соответствую­щем районе, спрос на определенную продукцию, объем перевозок и т.д. Условия игры с природой задаются в виде матрицы А:

(9.46)

Элемент матрицы равен выигрышу игрока I, если он использует стратегию а состояние природы

При решении задач игры с природой используют критерии для вы­бора оптимальных стратегий. Рассмотрим некоторые из них.

1. Критерий максимального математического ожидания (вероятно­стных оценок).

Если вероятности состояний природы Р_i известны, то критерием при­нятия решений является максимум математического ожидания выигры­ша (минимум математического ожидания риска):

(9.47)

(9.48)

где — математическое ожидание выигрыша; — вероятность со­стояния «природы»; — элементы чистой стратегии платежной мат­рицы А; — элементы i -той стратегии матрицы риска R.

 

2. Максиминный критерий Вальда. Этот критерий пессимизма, при котором выбирается стратегия, позволяющая получить выигрыш не меньше, чем

(9.49)

3. Критерий Гурвица определяет оптимальную стратегию по формуле

(9.50)

где — коэффициент пессимизма-оптимизма, величина которого опре­деляется из субъективных соображений и условия

4. Критерий минимальною риска Севиджа, согласно которому выби­рают стратегию, при которой величина риска принимает наименьшее значение в самой неблагоприятной ситуации, т.е.

(9.51)

Игрок ориентируется при этом не на выигрыш, а на минимально воз­можный риск потерь в связи с недостаточной информацией о реальной ситуации.

Пример 9.9.

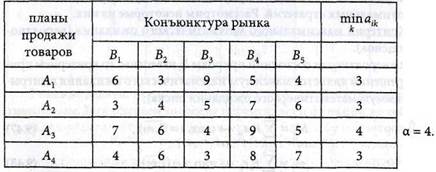
Определить оптимальный план продажи товаров с учетом изменяю­щейся конъюнктуры рынка и спроса покупателей, если величина прибы­ли указана в табл. 9.1.

Таблица 9.1

Решение

1.

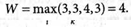Определяем оптимальную стратегию (план) по критерию Вальда (9.49):

Оптимальный план соответствует стратегии А₃.

2. Определяем план продажи товаров по вероятностному критерию (9.47), полагая состояния природы равновероятностными,

Вычисляем математическое ожидание выигрыша для принятия ре­шений:

М₁ = 6-0,2 + 3-0,2 + 9-0,2 + 5-0,2 + 4-0,2 = 5,4;

М₂ = 3 ∙ 0,2 + 4 ∙ 0,2 + 5 ∙ 0,2 + 7-0,2 + 6 ∙ 0,2 = 5,0;

М₃ = 7 ∙ 0,2 + 6 ∙ 0,2 + 4 ∙ 0,2 + 9-0,2 + 5 ∙ 0,2 = 6,2;

М₄ = 4 ∙ 0,2 + 6 ∙ 0,2 + 3 ∙ 0,2 + 8-0,2 + 7 ∙ 0,2 = 5,6;

 

Оптимальный план — А₃(9.51).

3. Чтобы воспользоваться критерием Севиджа (9.51), построим мат­рицу рисков R, элементы которой определяем по зависимости

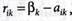
где — максимальный элемент в каждом столбце матрицы А.

В соответствии с этим критерием предполагается план продажи то­варов, соответствующий стратегиям А₁ и А₂.

4. Воспользуемся критерием Гурвица, полагая коэффициент песси­мизма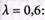

G₃= 0,6 ∙ 3 + (1-0,6) ∙ 9 = 5,4;

G₂ = 0,6 ∙ 3 + (1-0,6) ∙ 7 = 4,6;

 

G₃ = 0,64 + (1-0,6)-9 = 6,0;

G₄ = 0,6-3 + (1-0,6)-8 = 5,0,

Оптимальным планом является А₃ так как

Таким образом, по трем критериям оптимальным является третий план — А₃ и по одному — А₁ и А₂ Ответ: А₃.

Контрольные вопросы

1. Каковы основные определения и понятия теории игр?

2. Какие игры называются стратегическими?

3. Какие стратегии называются чистыми, активными и оптимальными?

4. Что определяет матричную игру в смешанных стратегиях?

5. Какие матричные игры можно решать графическим способом?

6. Как упрощаются платежные матрицы?

7. Каковы критерии принятия решений в условиях неопределенности?

8. Какие игры называются играми с «природой»?

ЗАДАЧИ 9.1-9.9

Найти решение игры в чистых стратегиях, если платежные матрицы заданы в виде:

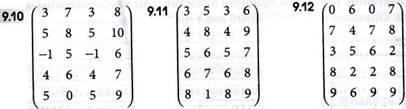
ЗАДАЧИ 9.10-9.24

Найти решение игры в смешанных стратегиях, если платежная мат­рица задана в виде:

 

 

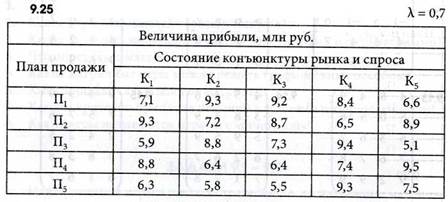
ЗАДАЧИ 9.25-9.29

Розничное торговое предприятие разработало несколько вариантов плана продажи товаров на предстоящей ярмарке с учетом меняющейся конъюнктуры рынка и спроса покупателей, получающиеся от их возмож­ных сочетаний. Величины прибыли представлены в виде матрицы выиг­рышей. Определить оптимальный план продажи товаров.

 

123	Поделиться:

Воспользуйтесь поиском по сайту: