 |
Основные геометрические характеристики сечений.
|
|
|
|
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
Методические указания по выполнению расчетно-проектировочных заданий для студентов машиностроительного факультета дневной формы обучения
Часть 1
Могилев 2008
УДК 539.3/6
ББК 30.121
С 64
Рекомендовано к опубликованию
учебно-методическим управлением
ГУ ВПО «Белорусско-Российский университет»
Одобрено кафедрой «Сопротивление материалов» «18» февраля 2008 г.,
протокол № 9
| Составители: канд. техн. наук, доц. А. А. Катькало; |
| ст. преподаватель В. А. Кемова; |
| канд. техн. наук, доц. В. А. Попковский |
Рецензент докт. техн. наук, доц. В. М. Пашкевич
Изложены требования, объем и последовательность расчетов при выполнении студентами машиностроительного факультета расчетно-проектировочных заданий по дисциплине «Сопротивление материалов».
Учебное издание
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
Часть 1
Ответственный за выпуск Д. М. Макаревич
Технический редактор А. Т. Червинская
Компьютерная верстка Н. П. Полевничая
Подписано в печать.Формат 60х84/16. Бумага офсетная. Гарнитура Таймс.
Печать трафаретная. Усл.- печ.л. Уч.-изд. л. Тираж 215 экз. Заказ №
Издатель и полиграфическое исполнение
Государственное учреждение высшего профессионального образования
«Белорусско-Российский университет»
ЛИ №02330/375 от 29.06.2004 г.
212005, г. Могилев, пр. Мира, 43
Ó ГУ ВПО «Белорусско-Российский
университет», 2008
| Содержание Введение.…………………………………………………………………. 1 Расчётно-проектировочное задание № 1. Геометрические характеристики плоских сечений……………………………………………. 1.1 Пример выполнения расчетно-проектировочного задания № 1...... 2 Расчетно-проектировочное задание № 2. Построение эпюр внутренних силовых факторов в статически определимых балках……….. 2.1 Пример выполнения расчетно-проектировочного задания № 2………………………………………………………………………………... 3 Расчетно-проектировочное задание № 3. Расчет статически определимой балки при изгибе………………………………………….…... 3.1 Пример выполнения расчетно-проектировочного задания № 3..… Список литературы…………………………………………………….... Приложение А.……………………..……………………………………. Приложение Б…………………………..……………………………….. Приложение В..…………………………………………………………. |
|
|
|
Введение
Целью выполнения расчетно-проектировочных заданий является закрепление у студентов теоретических знаний и приобретение навыков в определении геометрических характеристик плоских сечений, построении эпюр внутренних силовых факторов в балках и рамах, а также в расчетах элементов конструкций при плоском поперечном изгибе. В осеннем семестре студенты выполняют три расчетно-проектировочных задания (РПЗ).
Методические указания составлены в соответствии с рабочей программой курса "Сопротивление материалов" для студентов машиностроительного факультета дневной формы обучения.
Расчетно-проектировочные задания оформляются в виде пояснительной записки на листах бумаги формата А4. Листы используются с одной стороны, должны иметь рамку и основную надпись, выполненную по ГОСТ 2.303 - 68. Текстовая часть записки располагается на всем поле листа, ограниченном рамкой. Расчетно-проектировочное задание дополняется графическим листом, выполненным на чертежной бумаге формата А4 или А3. Расчетные схемы и эпюры выполняются карандашом, четко, с соблюдением правил оформления машиностроительных чертежей в соответствии с ГОСТ 2.104 - 68.
|
|
|
Комплект пояснительной записки должен включать:
–титульный лист;
–лист с заданием, который должен быть оформлен по принятой форме и подписан преподавателем и студентом;
– лист с исходными данными (выполняется по данным листа задания с указанием расчетной схемы, полных исходных данных и конечных целей задания);
–расчетно-текстовую часть, которая должна содержать необходимые технически грамотные пояснения к используемым формулам и выполненным расчетам. Сокращения слов не допускаются. При определении искомых величин необходимо записать формулы в символах, подставить их численные значения, записать результат и проставить его единицу измерения. Решение выполняется с точностью в зависимости от поставленной задачи. Расчеты ведутся в СИ;
–список литературы, который включает те источники, на которые в расчетно-текстовой части есть ссылки. Ссылка на литературу дается в квадратных скобках;
– графический лист, который сшивается с пояснительной запиской.
Задания, выполненные с нарушением указанных требований, не принимаются на проверку.
1 Расчетно-проектировочное задание № 1. Геометрические
Характеристики плоских сечений
Основные геометрические характеристики сечений.
Для расчета бруса на прочность, жесткость и устойчивость необходимо знать геометрические характеристики его поперечного сечения. Основные геометрические характеристики произвольного плоского поперечного сечения площадью F, представленного на рисунке 1.1, в системе координат XY приведены в таблице 1.1.
Рисунок 1.1 – К определению геометрических характеристик
Таблица 1.1 – Геометрические характеристики плоских сечений
| Геометрическая характеристика | Интегральная зависимость | Единица измерения |
| Площадь | 
| м2, см2 |
| Статический момент | 
| м3, см3 |
| Осевой момент инерции |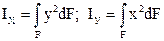 
| м4, см4 |
| Полярный момент инерции |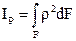  
| м4, см4 |
| Центробежный момент инерции |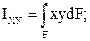 
| м4, см4 |
| Осевой момент сопротивления |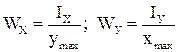 
| м3, см3 |
| Полярный момент сопротивления |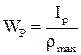 
| м3, см3 |
| Радиус инерции | 
| м, см |
Примечание.  - расстояния от осей до наиболее удаленных точек сечения,  - расстояние от полюса до наиболее удаленной точки сечения.
|
Для расчетов любой конструкции необходимо определять положение центра тяжести ее поперечного сечения. Для сложного или составного сечения общий центр тяжести можно определить по формулам
|
|
|
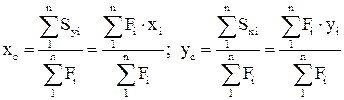, (1.1)
где n – количество простых фигур, составляющих сечение;
Fi – площадь простой фигуры, составляющей сечение;
Хi, Уi – координаты центра тяжести простой фигуры в выбранной (начальной) системе координат.
Выбор начальной системы координат не влияет на положение центра тяжести составного сечения, а сказывается только на знаках и значениях используемых в расчетах величин. Рекомендуется начало координат размещать в нижнем левом углу сечения или совмещать его с центром тяжести одной из заданных фигур. Следует также обратить внимание на то, что статический момент сохраняет алгебраический знак.
Через центр тяжести сечения проходят центральные оси сечения, которые обозначают Х с и У с. Если сечение имеет ось симметрии, то эта ось проходит через центр тяжести и является центральной. Моменты инерции относительно центральных осей обозначают 
и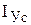 
. Статический момент инерции сечения относительно центральных осей инерции равен нулю. Центробежный момент инерции сечений, имеющих хотя бы одну ось симметрии, равен нулю.
Осевые моменты инерции и полярный момент инерции сечения всегда положительны, а центробежный момент инерции может быть как положительным, отрицательным, так и равняться нулю. Это правило распространяется на большинство простых геометрических фигур (прямоугольник, круг, равнобедренный треугольник и прочие) и на прокатные профили (двутавр, швеллер, уголки). Центробежный момент инерции уголка выбирается по данным сортамента или определяется по формуле
, (1.7)
где Imin – минимальный момент инерции уголка.
Правило знаков для центробежного момента инерции уголка представлено на рисунке 1.2.
|
| ||||
Рисунок 1.2 – Правило знаков центробежного момента инерции уголка
|
|
|
