 |
Расчеты на жесткость при изгибе
|
|
|
|
Проверка жесткости балки выполняется из условия жесткости
, (3.14)
где уmax – максимальный прогиб в опасном сечении балки;
– допускаемый прогиб балки;
L – длина пролета (расстояние между опорами).
Для определения деформаций в балках (прогибов и углов поворота) применяют метод начальных параметров, общий вид уравнений которого можно представить в виде выражений:
; (3.15)
,(3.16)
где 
– модуль упругости первого рода для заданного материала балки;
– осевой момент поперечного сечения балки;
EIx – выражение жесткости при изгибе;
Θ0, у0 – начальные угол поворота и прогиб соответственно (начальные параметры);
z – текущая координата рассматриваемого сечения;
a, b, c – расстояния от начала координат до точки приложения соответствующей нагрузки.
При расчете деформаций в уравнения метода начальных параметров включают нагрузки, действующие слева от рассматриваемого сечения, в том числе и реакции опор (заделки). Правило знаков для нагрузок, входящих в указанные уравнения, такое же, как и для определения знаков изгибающего момента. Если заданная распределенная нагрузка действует не до конца балки, то ее необходимо «компенсировать» такой же по величине и обратной по направлению компенсирующей распределенной нагрузкой начиная с того сечения, где прекратила действовать заданная нагрузка (на рисунке 3.1 она показана пунктиром).
Рисунок 3.1- Расчетная схема
В зависимости от способа закрепления крайнего левого сечения балки можно определить начальные параметры (см. таблицу 3.1).
Таблица 3.1 – Определение начальных параметров
| Способ закрепления балки | Начальные параметры | Искомый начальный параметр | Условия на опорах |
| 
| 
| 
|
| 
| 
| 
|
| 
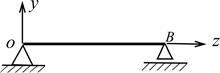
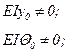
| нет |  не рассматриваются
|
|
|
| 
|
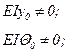
Пример выполнения задания
|
|
|
Исходные данные: схема балки с указанием численных величин нагрузок и линейных размеров, величины допускаемого нормального и касательного напряжений.
Требуется:
-подобрать поперечное сечение балки в виде двутавра из условия прочности по нормальным напряжениям, если допускаемое напряжение 
;
- проверить прочность выбранного двутаврового сечения по нормальным и касательным напряжениям, если допускаемое касательное напряжение 
;
- построить эпюры распределения нормальных и касательных напряжений в опасном сечении балки;
- проверить прочность балки по третьей теории прочности в опасном сечении;
- рассчитать величины главных напряжений и определить положение главных площадок в опасной точке;
- построить эпюру прогибов для заданной балки, используя уравнение метода начальных параметров;
- проверить жесткость балки;
- дать заключение о прочности и жесткости балки.
Вычерчиваем заданную балку с указанием внешних нагрузок и линейных размеров (рисунок 3.2). Определяем опорные реакции:
;
;
;
.
Проверка: 
.
Рисунок 3.2 – Расчетная схема балки
Разбиваем балку на характерные участки и строим эпюры поперечных сил и изгибающих моментов (рисунок 3.3, а, б).
1 участок: 
.
;
.
2 участок: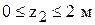 
.
;
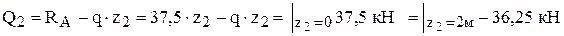Исследование на экстремум:
;
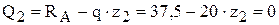откуда 
;
.
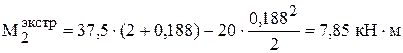3 участок: 
.
;
.
Максимальное значение изгибающего момента Mmax =25 кН∙м. Из условия прочности (3.2) рассчитываем величину осевого момента сопротивления поперечного сечения:
.
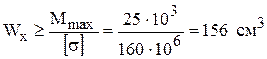По ГОСТ 8239-89 выбираем сечения с близкими значениями осевых моментов сопротивления: двутавр № 18 (
) и двутавр № 20 (
). Проверяем прочность выбранных двутавровых сечений по нормальным напряжениям, используя условие 3.2:
.
Найдем величину перенапряжения балки:
|
|
|
,
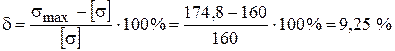что превышает допустимые 5 %. Следовательно, проверяем на прочность двутавр № 20:
-
условие прочности по нормальным напряжениям выполняется.
Рисунок 3. 3 – Расчетная схема балки и эпюры ВСФ и прогибов
Выписываем геометрические характеристики и размеры двутавра № 20: 
, 
, 
, 
, 
, 
.
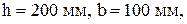
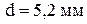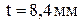Проверяем прочность выбранного двутаврового сечения по касательным напряжениям (формула (3.8)), если максимальное значение поперечной силы 
:
-
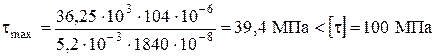условие прочности по касательным напряжениям выполняется.
Для анализа напряжений в поперечном сечении при плоском поперечном изгибе в качестве опасного выбираем опорное сечение В, в котором и изгибающий момент, и поперечная сила достигают максимального значения: 
и 
Поперечное сечение двутавра разбиваем на характерные точки A, B, C, D, E, F, K и определяем действующие в них величины нормальных напряжений по формуле (3.1)
;
;
;
;
.
Обращая внимание на то, что в опасном сечении растянуты верхние волокна, строим эпюру распределения нормальных напряжений по высоте двутавра (рисунок 3.4, б).
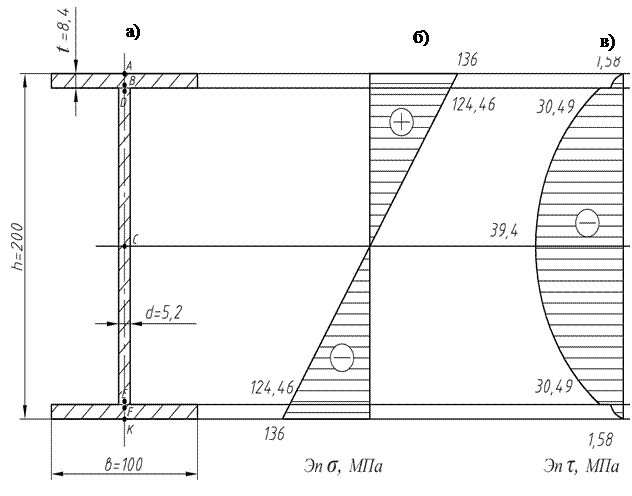
Рисунок 3.3 – Поперечное сечение балки, эпюры нормальных и касательных напряжений
Значения касательных напряжений определяем по формуле (3.7). Выше точки А сечение отсутствует, поэтому для сечения, лежащего выше этой точки, статический момент площади сечения равен нулю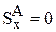 
. Над слоем, к которому принадлежит точка В и D, находится полка двутавра. Статический момент инерции полки двутавра:
.
Точка С делит двутавр на две половины, поэтому для нее берем статический момент площади полусечения (из сортамента)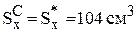 
.
Определяем величину касательных напряжений с учетом того, что ширина исследуемого слоя в исследуемых точках B и F равна ширине полки двутавра 
, а в точках E и D - 
:
;
;
;
.
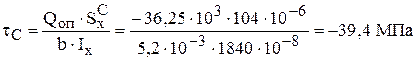Строим эпюру распределения касательных напряжений (рисунок 3.4, в).
Проверяем прочность балки по третьей теории прочности в опасном сечении по формуле (3.9):
Условие прочности выполняется.
Рассчитываем величины главных напряжений и определяем положение главных площадок в опасной точке D по формулам (3.11) и (3.13), для которой 
и 
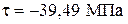(рисунок 3.4). Экстремальные напряжения рассчитываются по:
|
|
|
;
;
.
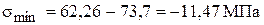Для нашего случая:
;
;
.
;
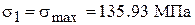– поворот происходит по часовой стрелке.
Рисунок 4.4 – Напряженное состояние в точке
Для построения эпюры прогибов для заданной балки, используем уравнение метода начальных параметров (4.13). Так как в начале координат находится опора, то начальный прогиб 
(см. таблицу 4.1). Применительно к рассматриваемой балке (см. рисунок 3.3, а) уравнение прогибов имеет вид:
;
Составляем уравнение прогибов для опоры В (z=4 м). Так как прогиб в ней должен отсутствовать, приравниваем составленное уравнение к нулю и определяем начальный угол поворота:
;
.
Вычисляем и строим эпюру прогибов в долях EIx, подставляя в уравнение прогибов различные значения z (рисунок 3.2, в):
;
;
;
;
;
Наибольшей величины прогиб достигает на краю консоли и равен
.
Определяем величину допускаемого прогиба по формуле (3.16):
.
Проверяем жесткость балки:
.
Условие жесткости выполняется.
Вывод: в качестве поперечного сечения балки выбран двутавр № 20, для которого выполняются условия прочности и жесткости.
Список литературы
1 Сопротивление материалов: метод. указания по использованию основных стандартов и справочных данных для студентов машиностроительных и строительных специальностей / Сост. И. А. Леонович, С. В. Гонорова, О. В. Гонорова.– Могилёв: Белорус.-Рос. ун-т, 2005. − 30 с.
2 Феодосьев, В. И. Сопротивление материалов / В. И. Феодосьев. − М.: Наука, 1986. − 512 c.
3 Дарков, А. В. Сопротивление материалов / А. В. Дарков, Г. С. Шпиро.− М.: Высш. шк., 1989. − 624 c.
4 Сопротивление материалов: учебник.: учебник / Под ред. Г. С. Писаренко. – 5-е изд., перераб. и доп. − Киев: Вища шк., 1986. − 775 c.
5 Беляев, Н. М. Сопротивление материалов / Н. М. Беляев. − М.: Наука, 1976.−530 c.
6 Буланов, Э. А. Решение задач по сопротивлению материалов / Э. А. Буланов.− М.: Высш шк., 1994. − 203 c.
7 Копнов, В. А. Сопротивление материалов: Руководство для решения задач и выполнения лабораторных и расчётно-графических работ / В. А. Копнов, С. Н. Кривошапко. – М.: Высш. шк., 2003. – 486 с.
|
|
|
8 Подскребко, М. Д. Сопротивление материалов / М. Д. Подскребко.− Минск: Дизайн ПРО, 1998. − 592 с.
9 Справочник по сопротивлению материалов / Под ред. Е. В. Винокурова.− Минск.: Навука і тэхніка, 1988. − 530 с.
10 ГОСТ 8239-89. Двутавры стальные горячекатаные. Cортамент черных металлов. Сортовой и фасонный прокат. Ч. 1. – М.: Изд-во стандартов. 1991. – 245 с.
|
|
|
